Method of Moments Solver for Metal and Dielectric Structures

Method of Moments computation technique for metal and dielectric antennas.

Antennas using dielectric substrate consists of a metal part and a dielectric part. The first step in the computational solution of electromagnetic problems is to discretize Maxwell's equations. The process results in this matrix-vector system:

$V = Z I$

V — Applied voltage vector. This signal can be voltage or power applied to the antenna or an incident signal falling on the antenna.
I — Current vector that represents current on the antenna surface.
Z — Interaction matrix or impedance matrix that relates V to I. For calculating the interaction matrix, the effect of metal and dielectric parts in an antenna are taken separately.

Antenna Toolbox™ uses method of moments (MoM) to calculate the interaction matrix and solve system equations.

MoM Formulation

The MoM formulation is split into three parts.

Discretization of Dielectrics

Discretization enables the formulation from the continuous domain to the discrete domain. This step is called meshing in antenna literature. In the MoM formulation, the metal surface of the antenna is meshed into triangles and the dielectric volume is meshed into tetrahedrons.

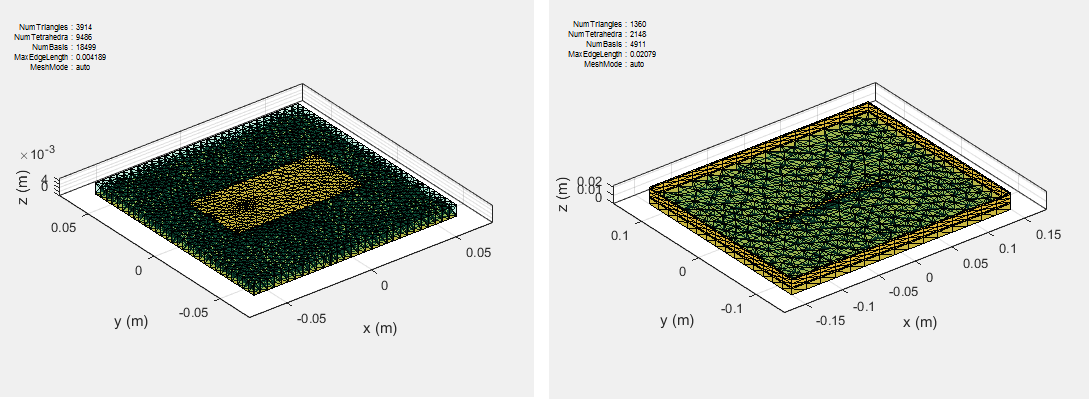
Images showing the meshed PCB antenna structures.

Basis Functions

Basis functions are used to represent unknown quantities. In the case of antennas using dielectrics, the unknown quantities are the surface current on the metal structure and flux density due to dielectric volume. Antenna Toolbox uses Rao-Wilton-Glisson (RWG) [2] basis functions. For basis functions for a metal structure in an antenna refer, Method of Moments Solver for Metal Structures.

For the dielectric volume of the antenna, Antenna Toolbox uses a zeroth order edge basis function to model the flux density.

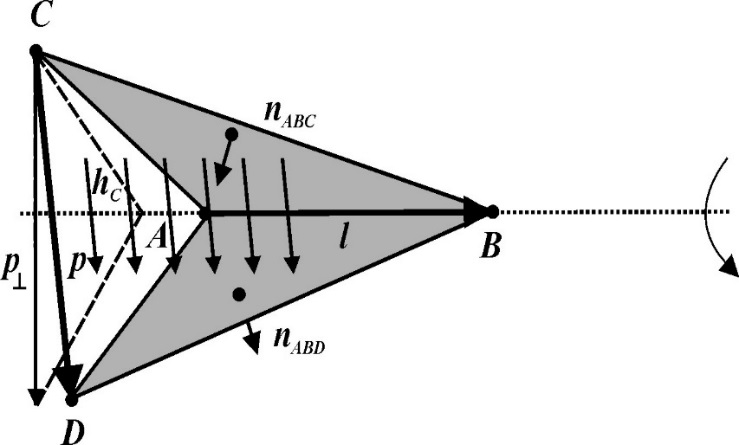
Diagram shows edge-based basis function model of the flux density.

The figure shows an edge-based basis function. The vector variation is perpendicular to the base edge AB (or $\bar{l}$ ). The vector of the edge CD (or $\bar{p}$ ) defines the basis function. Within a tetrahedron, the basis function is a constant field given by

$\vec{f} = c \vec{p}$

c – normalization coefficient.
p – vector of the edge defining the basis function.

Interaction Matrix

The interaction matrix is a complex dense symmetric matrix. For a metal-dielectric antenna, there are two sets of basis functions and four interactions. To fill out the interaction matrix, calculate the free-space Green's function between all the basis functions on the antenna surface. The final interaction matrix equations are:

Z_MM – metal to metal interaction. For a pure metal structure, you only calculate this symmetric square matrix.
$Z_{m n}^{M M} = (\frac{j ω μ}{4 π}) \int_{S} \int_{S} {\vec{f}}^{M}_{m} (\vec{r}) . {\vec{f}}^{M}_{n} (\vec{r^{'}}) g d \vec{r^{'}} d \vec{r} - (\frac{j}{4 π ω ε}) \int_{S} \int_{S} (\nabla . {\vec{f}}^{M}_{m}) (\nabla . {\vec{f}}^{M}_{n}) g d \vec{r^{'}} d \vec{r}$
Z_DD – dielectric to dielectric interaction. For pure dielectric structures, you only calculate this symmetric square matrix.
$\begin{array}{l} {\hat{Z}}_{m n}^{D D} = \sum_{p - 1}^{P} \sum_{p^{'} - 1}^{P^{'}} \frac{K_{p}}{{\hat{ε}}_{p}} \int_{V_{D}} {\vec{f}}_{m p} (\vec{r}) \cdot {\vec{f}}_{n p^{'}} (\vec{r}) d \vec{r} \\ - \frac{ω^{2} μ_{0}}{4 π} \sum_{p - 1}^{P} \sum_{p^{'} - 1}^{P^{'}} K_{p} K_{p^{'}} \int_{V_{D}} \int_{V_{D^{'}}} g (\vec{r}, \vec{r^{'}}) {\vec{f}}_{m p} (\vec{r}) \cdot {\vec{f}}_{n p^{'}} (\vec{r^{'}}) d \vec{r} d \vec{r^{'}} \\ - \frac{1}{4 π ε_{0}} \sum_{q - 1}^{Q} \sum_{q^{'} - 1}^{Q^{'}} {\hat{K}}_{q} {\hat{K}}_{q^{'}} \int_{Ω_{q}} \int_{Ω_{q^{'}}} g (\vec{r}, \vec{r^{'}}) f_{⊥ m q} (\vec{r}) f_{⊥ n q^{'}} (\vec{r^{'}}) d_{s} d_{s^{'}} m, n = 1, ...., N \end{array}$
Z_MD and Z_DM – These matrices calculate the interaction between metal and dielectric. This matrix is not a symmetrical square matrix.
$\begin{array}{l} Z_{m n}^{M D} = - \frac{ω^{2} μ_{0}}{4 π} \sum_{p - 1}^{2} \sum_{p^{'} - 1}^{P^{'}} K_{p} \int_{t} \int_{V_{D^{'}}} {\vec{f}}_{n}^{M} (\vec{r}) \cdot {\vec{f}}_{m p^{'}} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d \vec{r^{'}} d_{s} \\ - \frac{1}{4 π ε_{0}} \sum_{p - 1}^{2} \sum_{q - 1}^{Q} {\hat{K}}_{q} \int_{t_{D}} \int_{Ω_{q^{'}}} (\nabla_{s} \cdot {\vec{f}}_{n}^{M} (\vec{r})) f_{⊥ m q} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d_{Ω^{'}} d_{s} \\ m = 1, ...., N_{D}; n = 1, ..., N_{M} \end{array}$
$\begin{array}{l} Z_{m n}^{D M} = - \frac{j ω μ_{0}}{4 π} \sum_{p - 1}^{2} \sum_{p^{'} - 1}^{P^{'}} K_{p^{'}} \int_{V_{D}} \int_{S_{D^{'}}} {\vec{f}}_{n p} (\vec{r}) \cdot {\vec{f}}_{m}^{M} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d_{s^{'}} d \vec{r} \\ + \frac{1}{4 π ε_{0} ω} \sum_{p - 1}^{2} \sum_{q - 1}^{Q} {\hat{K}}_{q} \int_{Ω_{q}} \int_{S_{D^{'}}} f_{⊥ n q} (\vec{r}) \cdot (\nabla_{s} \cdot {\vec{f}}_{m}^{M} (\vec{r^{'}})) g (\vec{r}, \vec{r^{'}}) d_{s^{'}} d_{Ω} \\ m = 1, ...., N_{D}; n = 1, ..., N_{M} \end{array}$

where

$g (\vec{r}, \vec{r^{'}}) = \frac{\exp (- j k R)}{R}, R = | \vec{r} - \vec{r^{'}} |$ is the free space Green's function.
$K = \frac{{\hat{ε}}^{\pm} - ε_{0}}{{\hat{ε}}^{\pm}}$ is the complex dielectric constant within every tetrahedron.
${\hat{K}}_{q} = K_{+} - K_{-}$ is the differential contrast on every face of the tetrahedron.

For a composite metal structure, you must calculate all four matrices.

Neighbor Region

The figure shows a typical interaction matrix for a metal structure Z_MM with 256 basis functions.

The figure shows a typical interaction matrix for a metal structure ZMM with 256 basis functions.

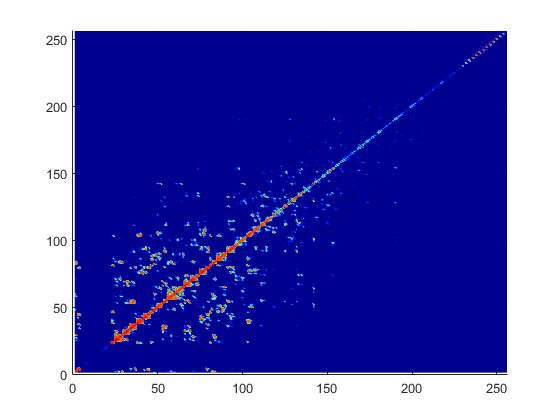
From the interaction matrix plot, you observe that the matrix is diagonally dominant. The dielectric interaction matrix is also diagonally dominant. As you move further away from the diagonal, the magnitude of the terms decreases. This behavior is same as the Green's function behavior. The Green's function decreases as the distance between r and r' increases. Therefore, it is important to calculate the region on the diagonal and close to the diagonal accurately.

This region on and around the diagonal is called neighbor region. For a metal-dielectric antenna, the neighborhood region is based on the average size of the tetrahedron.

For neighboring region details for metal antennas refer, Method of Moments Solver for Metal Structures.

Singularity Extraction

Along the diagonal, r and r' are identical and the defined Green's function becomes singular. To remove the singularity, extraction is performed on these terms. The equations for the singularity extraction of the Z_MM matrix are:

$\begin{array}{l} \int_{t_{p}} \int_{t_{q}} ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j}) g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1) ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s \\ \int_{t_{p}} \int_{t_{q}} g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d s' d s \end{array}$

The two integrals on the right side of the equations, called potential or static integrals are found using analytical results [3].

The equations for the singularity extraction of the Z_DD matrix are:

$\begin{array}{l} \int_{V_{D}} \int_{V_{D^{'}}} g (\vec{r}, \vec{r^{'}}) d \vec{r} d \vec{r^{'}} = \int_{V_{D}} \int_{V_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d \vec{r} d \vec{r^{'}} + \int_{V_{D}} \int_{V_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d \vec{r} d \vec{r^{'}} \\ \int_{Ω_{q}} \int_{Ω_{q^{'}}} g (\vec{r}, \vec{r^{'}}) d Ω d Ω' = \int_{Ω_{D}} \int_{Ω_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d Ω d Ω' + \int_{S_{D}} \int_{S_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d Ω d Ω \end{array}$

Finite Arrays

The MoM formulation for finite arrays is the same as for a single antenna element. The main difference is the number of excitations (feeds). For finite arrays, the voltage vector is now a voltage matrix. The number of columns are equal to the number of elements in the array.

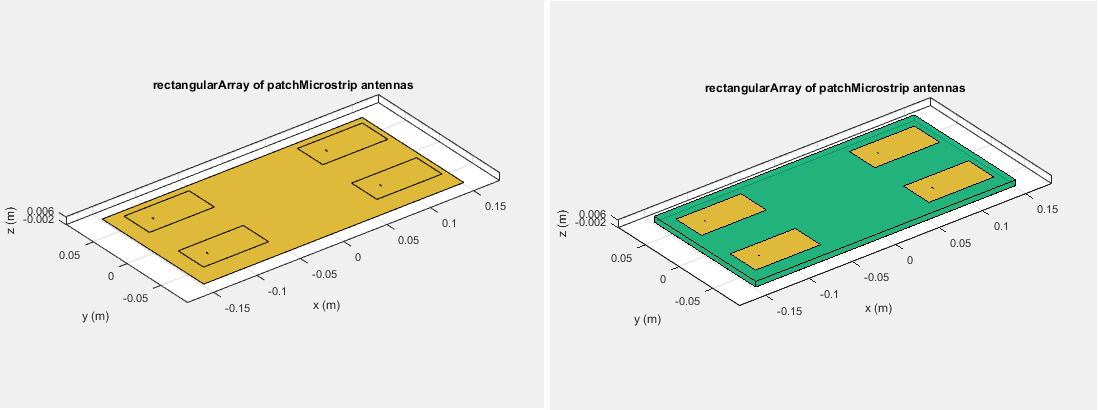
This figure shows a rectangular array of microstrip patch antenna with and without a dielectric substrate.

For example, the voltage vector matrix for a 2-by-2 array of rectangular patch antenna (with and without dielectric substrate) has four columns as each antenna can be excited separately.

Infinite Array

To model an infinite array, you change the MoM to account for the infinite behavior. To do so, you replace the free-space Green's functions with periodic Green's functions. The periodic Green's function is an infinite double summation.

Green's Function	Periodic Green's Function
$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = \| \vec{r} - {\vec{r}}^{'} \| \end{array}$	$\begin{array}{l} g_{periodic} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = - k (x_{m} \sin θ \cos φ + y_{n} \sin θ \sin φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

Green's Function

Periodic Green's Function

$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = | \vec{r} - {\vec{r}}^{'} | \end{array}$

$\begin{array}{l} g_{periodic} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = - k (x_{m} \sin θ \cos φ + y_{n} \sin θ \sin φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

d_x and d_y are the ground plane dimensions that define the x and y dimensions of the unit cell. θ and Φ are the scan angles.

Comparing the two Green's functions, you observe an additional exponential term that is added to the infinite sum. The Φ_mn accounts for the scanning of the infinite array. The periodic Green's function also accounts for the effect of mutual coupling.

For more information see, Infinite Arrays.

References

[1] Harringhton, R. F. Field Computation by Moment Methods. New York: Macmillan, 1968.

[2] Rao, S. M., D. R. Wilton, and A. W. Glisson. “Electromagnetic scattering by surfaces of arbitrary shape.” IEEE. Trans. Antennas and Propagation, Vol. AP-30, No. 3, May 1982, pp. 409–418.

[3] Wilton, D. R., S. M. Rao, A. W. Glisson, D. H. Schaubert, O. M. Al-Bundak. and C. M. Butler. “Potential Integrals for uniform and linear source distribution on polygonal and polyhedral domains.” IEEE. Trans. Antennas and Propagation. Vol. AP-30, No. 3, May 1984, pp. 276–281.

[4] Balanis, C.A. Antenna Theory. Analysis and Design. 3rd Ed. New York: John Wiley & Sons, 2005.