Train Machine Learning Model for Analysis of Custom Antenna
This example demonstrates how to apply machine learning to antenna analysis, and it illustrates a general recipe that you can use to train machine learning models to characterize antenna structures modeled and simulated in Antenna Toolbox™.
Overview of Machine Learning Workflow for Antenna Analysis
The overall workflow entails the following steps:
Model and parameterize the antenna structure in Antenna Toolbox.
Identify the tunable design variables (predictors) and analysis metrics (responses) for the machine learning model to learn.
Conduct a design of experiments (DOE) to get a representative collection of observations comprised of values for the design variables sampled within the ranges of interest.
Generate response data using full-wave simulation of the antenna for each parameter set.
Prepare and preprocess the data for training, tuning, and testing candidate machine learning models.
Iteratively train and optimize hyperparameters across various machine learning models to select an optimal model that has good predictive performance.
Assess the model's performance and prediction accuracy against full-wave simulation results.
In this example, the antenna of interest is the C-shaped microstrip patch antenna. As per [1] and [2], this antenna is constructed by cutting a rectangular slot at a radiating edge of a conventional rectangular patch antenna. The analysis metric of interest is the resonant frequency, defined here as the operating frequency at which the reflection coefficient magnitude (S11) is minimum. This example follows [2] and [3] in its adoption of the S11-based definition of resonant frequency. This is in contrast to the impedance-based definition, which defines the resonant frequency as the frequency at which the reactance is equal to zero.
Model and Parameterize Custom Antenna Structure
Define Parameter Sets for Antenna Design Variables
Specify the number of predictors, which correspond to the tunable design variables for the antenna.
numpreds = 7;
Define the combinations of antenna design parameters as provided in [2]. In this example, there are five sets of length/width values. For each length/width set, there are two possible slot lengths, two possible slot widths, and two possible slot offsets. This yields 5×2×2×2 = 40 configurations. For each of these configurations, there are two possible substrate heights and two possible dielectric constants. This yields a total of 40×2×2 = 160 antenna parameter sets. Note that the geometric parameters here are all specified in millimeters.
L = [30; 35; 40; 45; 50]; % Length (mm) W = [20; 25; 30; 35; 40]; % Width (mm) l = [10 20; 15 25; 15 30; 25 30; 20 40]; % Slot length (mm) w = [5 10; 7 12; 7.5 15; 5 10; 10 20]; % Slot width (mm) d = [3 6; 8 10; 5 10; 20 25; 7 14]; % Slot offset (mm) h = [1.6 2.5]; % Substrate height (mm) eR = [2.33 4.4]; % Substrate relative permittivity
View the sets of patch dimensions in table format to elucidate the correspondence between the sets of outer dimensions and the respectives choices of slot dimensions.
disp(table(L,W,l,w,d))
L W l w d
__ __ ________ __________ ________
30 20 10 20 5 10 3 6
35 25 15 25 7 12 8 10
40 30 15 30 7.5 15 5 10
45 35 25 30 5 10 20 25
50 40 20 40 10 20 7 14
Define Fixed Parameters for Antenna Feed
Specify the feed location in meters and the feed excitation voltage.
feedparams.x0 = 5e-3; % m feedparams.y0 = 5e-3; % m feedparams.V = 1; % V
Examine Antenna Structure
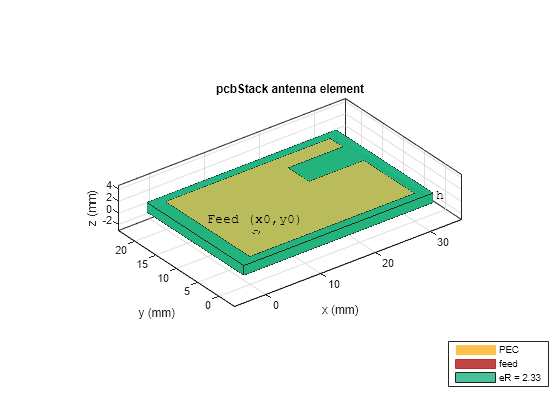
Use the helper function, createCShapedPatchAntenna, to create a PCB stack model of the antenna for the first of the 160 parameter sets. When calling the helper function, set Visualize=true to view the antenna's structure and parameterization. For all parameter sets in this example, the helper function specifies the ground plane dimensions as 1.15 times the respective outer dimensions of the radiating patch.
ant = createCShapedPatchAntenna(L(1),W(1),l(1,1),w(1,1),d(1,1),h(1),eR(1), ...
feedparams,Visualize=true);
Create Full Factorial Design to Assemble Table of Antenna Design Parameter Sets
Generate a full factorial design to account for the 160 antenna parameter configurations. Full factorial design is one type of DOE technique. In this example, the parameter combinations have been preselected from [2] as a representative distribution composed of discrete sets of values for each parameter. Accordingly, a full factorial design from the curated parameter sets is appropriate. Note that other DOE techniques exist to perform data collection in a parsimonious manner and/or from a continuous distribution of parameter values. For more information, see Design of Experiments (DOE) (Statistics and Machine Learning Toolbox).
dFF = fullfact([5 2 2 2 2 2])
dFF = 160×6
1 1 1 1 1 1
2 1 1 1 1 1
3 1 1 1 1 1
4 1 1 1 1 1
5 1 1 1 1 1
1 2 1 1 1 1
2 2 1 1 1 1
3 2 1 1 1 1
4 2 1 1 1 1
5 2 1 1 1 1
⋮
N = height(dFF)
N = 160
The structure of dFF, the full factorial design matrix, is as follows:
The first column of
dFFcontains the indices for the sets of outer dimensions, namely the length (L) and the width (W) values.The second, third, and fourth columns of
dFFcontain the indices to specify the choice of slot dimensions, namely the slot length (l), slot width (w), and slot offset (d), respectively, corresponding to the choice of outer dimensions. In particular, when indexing intol,w, andd, use the first column ofdFFto adhere to the correspondence between the combinations of slot dimensions and the sets of outer dimensions.The fifth and sixth columns of
dFFcontain the indices for the sets of substrate height (h) and relative permittivity (eR) values, respectively.
Use this full factorial design to construct a table of predictor values. For completeness, capture the units for the predictor variables in the table properties.
T0 = array2table(zeros(N,numpreds), ... VariableNames=["L","W","l","w","d","h","eR"],RowNames=string(1:N)); for idx = 1:N rowIdx = dFF(idx,1); T0.L(idx) = L(rowIdx); T0.W(idx) = W(rowIdx); T0.l(idx) = l(rowIdx,dFF(idx,2)); T0.w(idx) = w(rowIdx,dFF(idx,3)); T0.d(idx) = d(rowIdx,dFF(idx,4)); T0.h(idx) = h(dFF(idx,5)); T0.eR(idx) = eR(dFF(idx,6)); end T0.Properties.VariableUnits = ["mm","mm","mm","mm","mm","mm",""]
T0=160×7 table
L W l w d h eR
__ __ __ ___ __ ___ ____
1 30 20 10 5 3 1.6 2.33
2 35 25 15 7 8 1.6 2.33
3 40 30 15 7.5 5 1.6 2.33
4 45 35 25 5 20 1.6 2.33
5 50 40 20 10 7 1.6 2.33
6 30 20 20 5 3 1.6 2.33
7 35 25 25 7 8 1.6 2.33
8 40 30 30 7.5 5 1.6 2.33
9 45 35 30 5 20 1.6 2.33
10 50 40 40 10 7 1.6 2.33
11 30 20 10 10 3 1.6 2.33
12 35 25 15 12 8 1.6 2.33
13 40 30 15 15 5 1.6 2.33
14 45 35 25 10 20 1.6 2.33
15 50 40 20 20 7 1.6 2.33
16 30 20 20 10 3 1.6 2.33
⋮
Generate Data Using Full-Wave Simulation
Define Simulation Parameters for Antenna Port Analysis
Specify the simulation frequency sweep across which to compute the antenna's frequency response: 1–5 GHz with a resolution of 50 MHz.
f = 1e9:50e6:5e9;
Generate Raw Data for S-Parameter and Impedance Frequency Responses
You can load the pregenerated data set from the file, CShapedPatchAntennaS11Data.zip, that is included with this example, or you can regenerate the data using the generateObservation helper function. In the latter case, you can optionally parallelize the data generation process if you have a Parallel Computing Toolbox™ license. Note that data regeneration can take several hours to complete. For each observation, the generateObservation helper function first calls the createCShapedPatchAntenna helper function to create the antenna structure and then performs full-wave simulation to compute the complex-valued S-parameter response over the frequency sweep specified by f. Use the interactive drop-down controls in this example to modify the data generation preferences.
S = cell(N,1); switch"LoadGeneratedData" case "LoadGeneratedData" foldername = "data"; if ~isfolder(foldername) unzip CShapedPatchAntennaS11Data.zip end files = dir(fullfile(foldername,"*.mat")); for idx = 1:N filename = files(idx).name; data = load(fullfile(foldername,filename),"S"); S{idx} = data.S; end case "RegenerateData" if
false parfor idx = 1:N [S{idx},~] = generateObservation(T0(idx,:),feedparams,f, ... SaveDataToFile=
true,FileIndex=idx); end else for idx = 1:N [S{idx},~] = generateObservation(T0(idx,:),feedparams,f, ... SaveDataToFile=
true,FileIndex=idx); end end end
Perform Feature Extraction to Obtain Resonant Frequency Values from Raw Data
As per [2] and [3], search for resonances within 1.15–3.335 GHz, as the antenna parameter ranges are selected for ultra-high frequency (UHF) applications.
jdx = find(f >= 1.15e9 & f <= 3.335e9); fs = f(jdx);
In particular, look for local minima in the |S11| responses within the 1.15–3.335 GHz frequency range. For each antenna, select the lowest frequency corresponding to an |S11| local minimum as the resonant frequency of interest, as this corresponds to the fundamental resonance.
fR = zeros(N,1); for idx = 1:N S11 = S{idx}.Parameters; S11 = 20*log10(abs(S11)); S11 = S11(jdx); kdx = find(islocalmin(S11),1); fR(idx) = fs(kdx); end
Prepare and Preprocess Data for Training and Testing
Assemble Predictor and Response Data into Table Format
Rescale the resonant frequency values to units of GHz, and then add them to the table as the response data.
T = addvars(T0,fR/1e9,NewVariableNames="fR"); T.Properties.VariableUnits(end) = "GHz"
T=160×8 table
L W l w d h eR fR
__ __ __ ___ __ ___ ____ ____
1 30 20 10 5 3 1.6 2.33 3.2
2 35 25 15 7 8 1.6 2.33 2.25
3 40 30 15 7.5 5 1.6 2.33 2.5
4 45 35 25 5 20 1.6 2.33 1.45
5 50 40 20 10 7 1.6 2.33 1.6
6 30 20 20 5 3 1.6 2.33 2.1
7 35 25 25 7 8 1.6 2.33 1.55
8 40 30 30 7.5 5 1.6 2.33 1.35
9 45 35 30 5 20 1.6 2.33 1.25
10 50 40 40 10 7 1.6 2.33 1.85
11 30 20 10 10 3 1.6 2.33 3.1
12 35 25 15 12 8 1.6 2.33 2.25
13 40 30 15 15 5 1.6 2.33 2.1
14 45 35 25 10 20 1.6 2.33 1.5
15 50 40 20 20 7 1.6 2.33 1.55
16 30 20 20 10 3 1.6 2.33 2
⋮
Visualize and Explore Distribution of Data
Data examination and visualization comprise an important step in a machine learning workflow. Visually explore the data to understand its structure and distribution. This can help you assess the quality of the collected data set and familiarize with the overarching relationships therein. It can also help you assess, compare, interpret, and/or contextualize the predictions eventually made by the trained models. This example presents two such visualization tools: histogram plots and parallel coordinates plots. For more information about these and other visualization tools, see Data Distribution Plots and Statistical Visualization (Statistics and Machine Learning Toolbox).
Create Histogram Plot
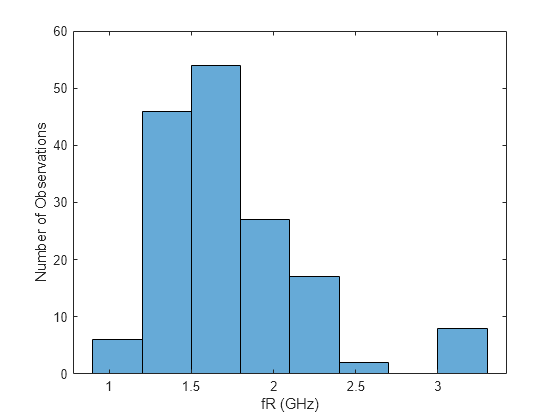
Create a histogram plot with automatic binning to understand the overall distribution of the response data.
figure hhist = histogram(T.fR); xlabel("fR (GHz)") ylabel("Number of Observations")
Create Parallel Coordinates Plot
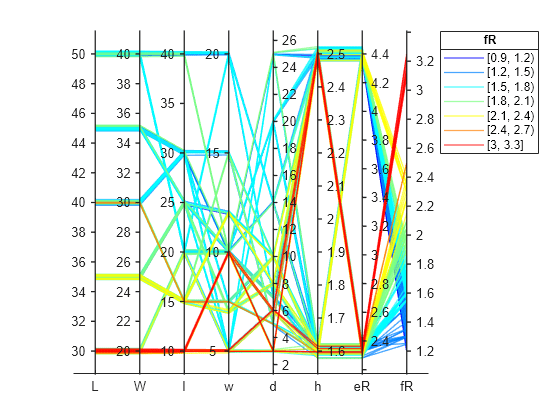
Create a parallel coordinates plot from the table, T, to visualize the multivariate relationships present in the data. Use the discretize function to bin the response values according to the bins automatically selected by the histogram function. Append the set of binned response values to the source table of the parallel coordinates plot, sort this source table according to the binning, and then group and color code the lines in the plot accordingly. Use the jet colormap to assign a distinct color to each binned group.
figure hpcplot = parallelplot(T,CoordinateVariables=1:width(T)); fR_group = discretize(T.fR,hhist.BinEdges,"categorical"); hpcplot.SourceTable.fR_group = fR_group; hpcplot.SourceTable = sortrows(hpcplot.SourceTable, ... ["fR_group","L","W","l","w","d","h","eR"]); hpcplot.GroupVariable = "fR_group"; hpcplot.LegendTitle = "fR"; hpcplot.Color = jet(hhist.NumBins);
Partition Data into Training and Test Sets
Use cvpartition with the Holdout parameter to randomly partition the data into a training set containing 80% of the observations and a test set containing 20% of the observations. Use the former to train and tune the machine learning model, and use the latter to test the performance of the trained model on new data. Stratify the partition according to the binning groups in fR_group to balance the response distribution across the training and test data sets and to achieve consistency of each with the distribution of the overall data. For the sake of reproducibility, set the random number generator seed to 1.
rng(1) partition = cvpartition(fR_group,HoldOut=0.2,Stratify=true); idxTrain = training(partition); idxTest = test(partition); dataTrain = T(idxTrain,:)
dataTrain=130×8 table
L W l w d h eR fR
__ __ __ ___ __ ___ ____ ____
1 30 20 10 5 3 1.6 2.33 3.2
2 35 25 15 7 8 1.6 2.33 2.25
4 45 35 25 5 20 1.6 2.33 1.45
5 50 40 20 10 7 1.6 2.33 1.6
6 30 20 20 5 3 1.6 2.33 2.1
8 40 30 30 7.5 5 1.6 2.33 1.35
9 45 35 30 5 20 1.6 2.33 1.25
10 50 40 40 10 7 1.6 2.33 1.85
11 30 20 10 10 3 1.6 2.33 3.1
12 35 25 15 12 8 1.6 2.33 2.25
13 40 30 15 15 5 1.6 2.33 2.1
14 45 35 25 10 20 1.6 2.33 1.5
15 50 40 20 20 7 1.6 2.33 1.55
16 30 20 20 10 3 1.6 2.33 2
17 35 25 25 12 8 1.6 2.33 1.55
19 45 35 30 10 20 1.6 2.33 1.3
⋮
dataTest = T(idxTest,:)
dataTest=30×8 table
L W l w d h eR fR
__ __ __ ___ __ ___ ____ ____
3 40 30 15 7.5 5 1.6 2.33 2.5
7 35 25 25 7 8 1.6 2.33 1.55
18 40 30 30 15 5 1.6 2.33 1.3
24 45 35 25 5 25 1.6 2.33 1.6
39 45 35 30 10 25 1.6 2.33 2
40 50 40 40 20 14 1.6 2.33 1.75
41 30 20 10 5 3 2.5 2.33 3.25
44 45 35 25 5 20 2.5 2.33 1.5
56 30 20 20 10 3 2.5 2.33 2.05
58 40 30 30 15 5 2.5 2.33 1.3
59 45 35 30 10 20 2.5 2.33 1.3
62 35 25 15 7 10 2.5 2.33 2.25
73 40 30 15 15 10 2.5 2.33 2.1
87 35 25 25 7 8 1.6 4.4 1.9
98 40 30 30 15 5 1.6 4.4 1.6
103 40 30 15 7.5 10 1.6 4.4 1.5
⋮
Examine Distribution of Response Values of Training vs. Test Data
It is important for the training data set to be statistically representative of the overall data so as not to bias or skew the model from learning how to generalize. It is also important for the test data set to be statistically similar to the training data set. Otherwise, the model's performance on the test data may not be a good indicator of the model's ability to generalize to new data drawn from the same population.
Compare the distribution of the response values in the training vs. test data sets to assess the degree of parity between the two. This example presents three visualization tools to perform this comparison: box plots, cumulative distribution plots, and histogram plots.
Create Box Plots
Create box charts of the response values from the overall data, training data, and test data.
figure htlb = tiledlayout(1,3); title(htlb,"Response Distribution") ylabel(htlb,"fR (GHz)") nexttile boxchart(T.fR) title("Overall Data") ylim([1 3.5]) nexttile boxchart(dataTrain.fR) title("Training Data") ylim([1 3.5]) nexttile boxchart(dataTest.fR) title("Test Data") ylim([1 3.5])
Create Cumulative Distribution Plots
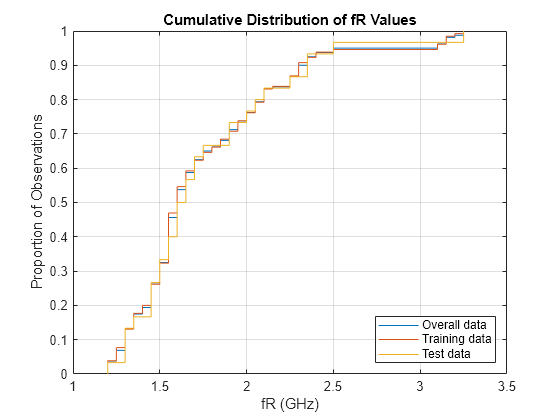
Create cumulative distribution plots of the response values from the overall data, training data, and test data.
figure cdfplot(T.fR) hold on cdfplot(dataTrain.fR) cdfplot(dataTest.fR) hold off xlabel("fR (GHz)") ylabel("Proportion of Observations") title("Cumulative Distribution of fR Values") legend("Overall data","Training data","Test data",Location="southeast")
Create Histogram Plots
Create histograms of the response values from the overall data, training data, and test data. Use the same bin edges and normalization method across all plots.
figure htlh = tiledlayout(1,3); title(htlh,"Response Distribution") xlabel(htlh,"fR (GHz)") ylabel(htlh,"Proportion of Observations") nexttile histogram(T.fR,BinEdges=hhist.BinEdges,Normalization="probability") title("Overall data") nexttile histogram(dataTrain.fR,BinEdges=hhist.BinEdges,Normalization="probability") title("Training data") nexttile histogram(dataTest.fR,BinEdges=hhist.BinEdges,Normalization="probability") title("Test data")
Use AutoML to Automatically Select and Train Regression Model with Optimized Hyperparameters
Statistics and Machine Learning Toolbox™ supports automated machine learning (AutoML) capabilities to automate, accelerate, and streamline the iterative process of model selection, configuration, hyperparameter tuning, optimization, examination, and visualization. This example focuses on the command-line workflow using the fitrauto (Statistics and Machine Learning Toolbox) function to automatically train and tune a selection of regression model types and hyperparameter values. That said, the software also supports interactive workflows within the Regression Learner App (Statistics and Machine Learning Toolbox). Refer to the following pages for more information:
Automated Regression Model Selection with Bayesian and ASHA Optimization (Statistics and Machine Learning Toolbox)
Train Regression Models in Regression Learner App (Statistics and Machine Learning Toolbox)
Train Model Using fitrauto
Use the fitrauto function to iteratively train and tune a variety of regression model types. The distribution of the training data suggests that a nonlinear model is more suitable than a linear model. Accordingly, set the Learners parameter to instruct fitrauto to consider only the following nonlinear types of models: Gaussian process, kernel, neural network, and support vector machine regression models.
In this example, use fitrauto with its default optimization algorithm, Bayesian Optimization (Statistics and Machine Learning Toolbox). In addition, you can customize the hyperparameter optimization options.
Set
MaxObjectiveEvaluationsto60to limit the number of iterations and indirectly limit the runtime. Otherwise, the software defaults to 30 iterations per learner, which in this case is 30×4 = 120 iterations. Alternatively, you can setMaxTimeto directly impose a time limit, which otherwise isInfby default.Set
UseParalleltotrueto accelerate the automated model tuning process. This option requires Parallel Computing Toolbox.Set
Repartitiontotrueto repartition the data in every iteration for cross-validation to improve optimization robustness and to account for partitioning noise.
rng(1) options.MaxObjectiveEvaluations = 60; % options.MaxTime = 300; options.UseParallel =false; options.Repartition = true; mdl = fitrauto(dataTrain,"fR",Learners=["gp","kernel","net","svm"], ... OptimizeHyperparameters="all",HyperparameterOptimizationOptions=options);
Learner types to explore: gp, kernel, net, svm Total iterations (MaxObjectiveEvaluations): 60 Total time (MaxTime): Inf |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 1 | Best | 1.1431 | 1.7709 | 1.1431 | 1.1431 | gp | Sigma: 0.00195 | | | | | | | | | BasisFunction: pureQuadratic | | | | | | | | | KernelFunction: squaredexponential | | | | | | | | | KernelScale: 32.553 | | | | | | | | | Standardize: false | | 2 | Best | 0.1291 | 0.5337 | 0.1291 | 0.1291 | svm | BoxConstraint: 0.25306 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.021507 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 3 | Best | 0.12334 | 1.0379 | 0.12334 | 0.12622 | svm | BoxConstraint: 5.0838 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.06554 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 4 | Best | 0.11966 | 6.2114 | 0.11966 | 0.11966 | net | Activations: none | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 2.413e-05 | | | | | | | | | LayerWeightsInitializer: glorot | | | | | | | | | LayerBiasesInitializer: ones | | | | | | | | | LayerSizes: [ 2 2 2 ] | | 5 | Accept | 0.19726 | 0.30717 | 0.11966 | 0.11966 | svm | BoxConstraint: 124.41 | | | | | | | | | KernelScale: 0.18687 | | | | | | | | | Epsilon: 34.636 | | | | | | | | | KernelFunction: gaussian | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: true | | 6 | Best | 0.054086 | 8.8242 | 0.054086 | 0.086131 | net | Activations: tanh | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 2.2974e-05 | | | | | | | | | LayerWeightsInitializer: glorot | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: 278 | | 7 | Best | 0.023394 | 0.7358 | 0.023394 | 0.035389 | gp | Sigma: 0.085687 | | | | | | | | | BasisFunction: linear | | | | | | | | | KernelFunction: ardrationalquadratic | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: true | | 8 | Accept | 0.20179 | 0.10564 | 0.023394 | 0.035389 | svm | BoxConstraint: 0.0056175 | | | | | | | | | KernelScale: 41.993 | | | | | | | | | Epsilon: 0.01849 | | | | | | | | | KernelFunction: gaussian | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 9 | Accept | 0.34939 | 9.7114 | 0.023394 | 0.035389 | svm | BoxConstraint: 0.44324 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.0018606 | | | | | | | | | KernelFunction: polynomial | | | | | | | | | PolynomialOrder: 2 | | | | | | | | | Standardize: false | | 10 | Accept | 0.11971 | 0.33362 | 0.023394 | 0.030707 | gp | Sigma: 0.15871 | | | | | | | | | BasisFunction: linear | | | | | | | | | KernelFunction: matern52 | | | | | | | | | KernelScale: 0.15479 | | | | | | | | | Standardize: false | | 11 | Accept | 0.20021 | 4.2722 | 0.023394 | 0.030707 | kernel | Learner: svm | | | | | | | | | KernelScale: 0.0016638 | | | | | | | | | Lambda: 0.00026298 | | | | | | | | | NumExpansionDimensions: 7941 | | | | | | | | | Epsilon: 0.032473 | | | | | | | | | Standardize: true | | 12 | Accept | 0.024156 | 1.0138 | 0.023394 | 0.028796 | gp | Sigma: 0.00011003 | | | | | | | | | BasisFunction: constant | | | | | | | | | KernelFunction: ardexponential | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 13 | Accept | 0.10522 | 0.27085 | 0.023394 | 0.028503 | gp | Sigma: 0.0010385 | | | | | | | | | BasisFunction: constant | | | | | | | | | KernelFunction: exponential | | | | | | | | | KernelScale: 1.0373 | | | | | | | | | Standardize: false | | 14 | Accept | 0.092551 | 0.27584 | 0.023394 | 0.028503 | svm | BoxConstraint: 12.608 | | | | | | | | | KernelScale: 127.27 | | | | | | | | | Epsilon: 0.0019437 | | | | | | | | | KernelFunction: gaussian | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 15 | Accept | 0.19943 | 0.48129 | 0.023394 | 0.028503 | kernel | Learner: leastsquares | | | | | | | | | KernelScale: 0.0012027 | | | | | | | | | Lambda: 0.0033154 | | | | | | | | | NumExpansionDimensions: 2586 | | | | | | | | | Epsilon: NaN | | | | | | | | | Standardize: false | | 16 | Accept | 0.038162 | 40.706 | 0.023394 | 0.028503 | net | Activations: sigmoid | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 1.0546e-06 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: ones | | | | | | | | | LayerSizes: [ 26 297 96 ] | | 17 | Accept | 0.12486 | 0.13734 | 0.023394 | 0.028503 | svm | BoxConstraint: 0.012055 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.0013756 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 18 | Accept | 0.52265 | 0.34702 | 0.023394 | 0.028503 | net | Activations: tanh | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 4.2685 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: [ 238 3 ] | | 19 | Accept | 0.19952 | 2.7617 | 0.023394 | 0.028503 | kernel | Learner: svm | | | | | | | | | KernelScale: 0.0048529 | | | | | | | | | Lambda: 1.2396e-05 | | | | | | | | | NumExpansionDimensions: 7358 | | | | | | | | | Epsilon: 0.00062171 | | | | | | | | | Standardize: true | | 20 | Accept | 0.12899 | 0.21681 | 0.023394 | 0.028503 | svm | BoxConstraint: 0.183 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.0071588 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 21 | Accept | 0.26055 | 0.049488 | 0.023394 | 0.028503 | svm | BoxConstraint: 380.24 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.92617 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 22 | Accept | 0.046787 | 3.811 | 0.023394 | 0.028503 | net | Activations: tanh | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 6.3728e-05 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: [ 10 4 ] | | 23 | Accept | 0.028375 | 0.45947 | 0.023394 | 0.026604 | gp | Sigma: 0.0016392 | | | | | | | | | BasisFunction: constant | | | | | | | | | KernelFunction: ardmatern52 | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: true | | 24 | Accept | 0.2064 | 2.1847 | 0.023394 | 0.026604 | kernel | Learner: svm | | | | | | | | | KernelScale: 0.0037044 | | | | | | | | | Lambda: 3.1774e-05 | | | | | | | | | NumExpansionDimensions: 8367 | | | | | | | | | Epsilon: 0.0018405 | | | | | | | | | Standardize: false | | 25 | Accept | 0.034719 | 2.0124 | 0.023394 | 0.026604 | net | Activations: tanh | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 0.012767 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: 25 | | 26 | Accept | 0.034976 | 1.0432 | 0.023394 | 0.026604 | net | Activations: sigmoid | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 2.5755e-06 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: 2 | | 27 | Accept | 0.1192 | 0.53417 | 0.023394 | 0.026391 | gp | Sigma: 0.9737 | | | | | | | | | BasisFunction: none | | | | | | | | | KernelFunction: ardsquaredexponential | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: true | | 28 | Accept | 0.063696 | 0.33932 | 0.023394 | 0.026391 | kernel | Learner: leastsquares | | | | | | | | | KernelScale: 1.4068 | | | | | | | | | Lambda: 0.0049323 | | | | | | | | | NumExpansionDimensions: 1419 | | | | | | | | | Epsilon: NaN | | | | | | | | | Standardize: true | | 29 | Accept | 0.11144 | 0.4175 | 0.023394 | 0.026391 | kernel | Learner: leastsquares | | | | | | | | | KernelScale: 32.938 | | | | | | | | | Lambda: 0.0001572 | | | | | | | | | NumExpansionDimensions: 2402 | | | | | | | | | Epsilon: NaN | | | | | | | | | Standardize: true | | 30 | Accept | 0.040308 | 0.27138 | 0.023394 | 0.026106 | gp | Sigma: 0.0056345 | | | | | | | | | BasisFunction: linear | | | | | | | | | KernelFunction: matern32 | | | | | | | | | KernelScale: 1.0556 | | | | | | | | | Standardize: true | | 31 | Accept | 0.19726 | 0.084515 | 0.023394 | 0.026106 | svm | BoxConstraint: 1.4828 | | | | | | | | | KernelScale: 0.0015252 | | | | | | | | | Epsilon: 5.2564 | | | | | | | | | KernelFunction: gaussian | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: true | | 32 | Accept | 0.06151 | 0.81542 | 0.023394 | 0.025584 | gp | Sigma: 0.00015957 | | | | | | | | | BasisFunction: none | | | | | | | | | KernelFunction: ardsquaredexponential | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 33 | Accept | 0.050137 | 0.094581 | 0.023394 | 0.025584 | svm | BoxConstraint: 0.0081331 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.0022615 | | | | | | | | | KernelFunction: polynomial | | | | | | | | | PolynomialOrder: 3 | | | | | | | | | Standardize: true | | 34 | Accept | 0.046793 | 3.3804 | 0.023394 | 0.025584 | net | Activations: sigmoid | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 1.8524e-05 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: ones | | | | | | | | | LayerSizes: [ 24 7 ] | | 35 | Accept | 0.11973 | 1.2916 | 0.023394 | 0.025584 | svm | BoxConstraint: 7.2223 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.094292 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 36 | Best | 0.023291 | 0.71714 | 0.023291 | 0.024505 | gp | Sigma: 0.0073413 | | | | | | | | | BasisFunction: none | | | | | | | | | KernelFunction: ardexponential | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 37 | Accept | 0.21785 | 0.39572 | 0.023291 | 0.024505 | kernel | Learner: svm | | | | | | | | | KernelScale: 5.0162 | | | | | | | | | Lambda: 0.054732 | | | | | | | | | NumExpansionDimensions: 2048 | | | | | | | | | Epsilon: 8.4213 | | | | | | | | | Standardize: true | | 38 | Accept | 0.026039 | 1.2096 | 0.023291 | 0.023577 | gp | Sigma: 0.049675 | | | | | | | | | BasisFunction: none | | | | | | | | | KernelFunction: ardrationalquadratic | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 39 | Accept | 0.027346 | 0.57973 | 0.023291 | 0.023625 | gp | Sigma: 0.012329 | | | | | | | | | BasisFunction: linear | | | | | | | | | KernelFunction: ardmatern32 | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 40 | Accept | 0.19701 | 0.25111 | 0.023291 | 0.023625 | net | Activations: sigmoid | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 0.072804 | | | | | | | | | LayerWeightsInitializer: glorot | | | | | | | | | LayerBiasesInitializer: ones | | | | | | | | | LayerSizes: [ 5 13 ] | |================================================================================================================================================| | Iter | Eval | log(1+valLoss)| Time for training | Observed min | Estimated min | Learner | Hyperparameter: Value | | | result | | & validation (sec)| validation loss | validation loss | | | |================================================================================================================================================| | 41 | Accept | 0.15568 | 0.18366 | 0.023291 | 0.023625 | kernel | Learner: svm | | | | | | | | | KernelScale: 7.5423 | | | | | | | | | Lambda: 0.30777 | | | | | | | | | NumExpansionDimensions: 268 | | | | | | | | | Epsilon: 0.17679 | | | | | | | | | Standardize: false | | 42 | Accept | 0.035996 | 0.42817 | 0.023291 | 0.023956 | gp | Sigma: 0.00017121 | | | | | | | | | BasisFunction: none | | | | | | | | | KernelFunction: rationalquadratic | | | | | | | | | KernelScale: 27.031 | | | | | | | | | Standardize: true | | 43 | Accept | 0.086826 | 0.30832 | 0.023291 | 0.023449 | gp | Sigma: 0.0082691 | | | | | | | | | BasisFunction: linear | | | | | | | | | KernelFunction: matern32 | | | | | | | | | KernelScale: 0.59347 | | | | | | | | | Standardize: false | | 44 | Accept | 0.2763 | 0.15718 | 0.023291 | 0.023449 | kernel | Learner: leastsquares | | | | | | | | | KernelScale: 0.030462 | | | | | | | | | Lambda: 7.1083e-05 | | | | | | | | | NumExpansionDimensions: 465 | | | | | | | | | Epsilon: NaN | | | | | | | | | Standardize: true | | 45 | Accept | 0.21785 | 0.46604 | 0.023291 | 0.023449 | kernel | Learner: svm | | | | | | | | | KernelScale: 386.19 | | | | | | | | | Lambda: 2.8961e-05 | | | | | | | | | NumExpansionDimensions: 119 | | | | | | | | | Epsilon: 16.863 | | | | | | | | | Standardize: false | | 46 | Accept | 0.10903 | 1.6691 | 0.023291 | 0.023449 | net | Activations: relu | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 0.333 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: ones | | | | | | | | | LayerSizes: 79 | | 47 | Accept | 0.19725 | 0.56871 | 0.023291 | 0.023795 | gp | Sigma: 2.1212 | | | | | | | | | BasisFunction: constant | | | | | | | | | KernelFunction: ardmatern32 | | | | | | | | | KernelScale: NaN | | | | | | | | | Standardize: false | | 48 | Accept | 0.1204 | 21.49 | 0.023291 | 0.023795 | net | Activations: tanh | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 3.8765e-06 | | | | | | | | | LayerWeightsInitializer: glorot | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: [ 72 227 ] | | 49 | Accept | 0.041297 | 9.0676 | 0.023291 | 0.023795 | net | Activations: relu | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 0.00099407 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: [ 141 5 ] | | 50 | Accept | 0.036173 | 5.0913 | 0.023291 | 0.023795 | kernel | Learner: svm | | | | | | | | | KernelScale: 5.1102 | | | | | | | | | Lambda: 0.00041644 | | | | | | | | | NumExpansionDimensions: 8193 | | | | | | | | | Epsilon: 0.022511 | | | | | | | | | Standardize: true | | 51 | Accept | 0.17841 | 0.14883 | 0.023291 | 0.023795 | kernel | Learner: leastsquares | | | | | | | | | KernelScale: 3.6977 | | | | | | | | | Lambda: 0.25232 | | | | | | | | | NumExpansionDimensions: 622 | | | | | | | | | Epsilon: NaN | | | | | | | | | Standardize: false | | 52 | Accept | 1.3328 | 0.12753 | 0.023291 | 0.023795 | net | Activations: sigmoid | | | | | | | | | Standardize: true | | | | | | | | | Lambda: 36.427 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: 3 | | 53 | Accept | 0.036252 | 2.5785 | 0.023291 | 0.023795 | net | Activations: relu | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 0.0048966 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: [ 8 11 9 ] | | 54 | Accept | 0.14747 | 0.061083 | 0.023291 | 0.023795 | svm | BoxConstraint: 4.6144 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.71107 | | | | | | | | | KernelFunction: linear | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: false | | 55 | Accept | 0.20749 | 0.089253 | 0.023291 | 0.023795 | svm | BoxConstraint: 0.19272 | | | | | | | | | KernelScale: 0.029708 | | | | | | | | | Epsilon: 0.00058854 | | | | | | | | | KernelFunction: gaussian | | | | | | | | | PolynomialOrder: NaN | | | | | | | | | Standardize: true | | 56 | Accept | 0.21758 | 0.086526 | 0.023291 | 0.023795 | kernel | Learner: svm | | | | | | | | | KernelScale: 0.0013155 | | | | | | | | | Lambda: 4.6138 | | | | | | | | | NumExpansionDimensions: 175 | | | | | | | | | Epsilon: 0.0019524 | | | | | | | | | Standardize: false | | 57 | Accept | 0.09557 | 1.4456 | 0.023291 | 0.023795 | net | Activations: relu | | | | | | | | | Standardize: false | | | | | | | | | Lambda: 0.0069746 | | | | | | | | | LayerWeightsInitializer: he | | | | | | | | | LayerBiasesInitializer: zeros | | | | | | | | | LayerSizes: 2 | | 58 | Accept | 0.063887 | 0.48024 | 0.023291 | 0.023795 | kernel | Learner: svm | | | | | | | | | KernelScale: 15.194 | | | | | | | | | Lambda: 0.0046916 | | | | | | | | | NumExpansionDimensions: 1449 | | | | | | | | | Epsilon: 0.32211 | | | | | | | | | Standardize: false | | 59 | Accept | 0.19971 | 0.9894 | 0.023291 | 0.023795 | kernel | Learner: svm | | | | | | | | | KernelScale: 0.0073665 | | | | | | | | | Lambda: 0.0069616 | | | | | | | | | NumExpansionDimensions: 3842 | | | | | | | | | Epsilon: 0.069355 | | | | | | | | | Standardize: false | | 60 | Accept | 0.19726 | 18.944 | 0.023291 | 0.023795 | svm | BoxConstraint: 724.18 | | | | | | | | | KernelScale: NaN | | | | | | | | | Epsilon: 0.061154 | | | | | | | | | KernelFunction: polynomial | | | | | | | | | PolynomialOrder: 4 | | | | | | | | | Standardize: false | __________________________________________________________ Optimization completed. Total iterations: 60 Total elapsed time: 228.7402 seconds Total time for training and validation: 164.3777 seconds Best observed learner is a gp model with: Learner: gp Sigma: 0.0073413 BasisFunction: none KernelFunction: ardexponential KernelScale: NaN Standardize: false Observed log(1 + valLoss): 0.023291 Time for training and validation: 0.71714 seconds Best estimated learner (returned model) is a gp model with: Learner: gp Sigma: 0.0073413 BasisFunction: none KernelFunction: ardexponential KernelScale: NaN Standardize: false Estimated log(1 + valLoss): 0.023795 Estimated time for training and validation: 0.71702 seconds Documentation for fitrauto display
Examine the automatically-selected model. This model is ready to make predictions for new observations.
disp(mdl)
CompactRegressionGP
PredictorNames: {'L' 'W' 'l' 'w' 'd' 'h' 'eR'}
ResponseName: 'fR'
CategoricalPredictors: []
ResponseTransform: 'none'
KernelFunction: 'ARDExponential'
KernelInformation: [1x1 struct]
BasisFunction: 'None'
Beta: [0x1 double]
Sigma: 0.0073
PredictorLocation: []
PredictorScale: []
Alpha: [130x1 double]
ActiveSetVectors: [130x7 double]
PredictMethod: 'Exact'
ActiveSetSize: 130
Assess Performance of Machine Learning Model
Evaluate Trained Model on Training Data Set
As a preliminary assessment of the performance, evaluate the model with the data used to train it. This helps to confirm that the model incorporates sufficient complexity to accurately fit the training data. Generally, you can expect good prediction accuracy here. Otherwise, the model suffers from the problem of underfitting.
Compute Percent Error in Model Predictions
Use the model's predict function on the training data, and compute the prediction error for each observation.
fR_predicted = predict(mdl,dataTrain); fR_actual = dataTrain.fR; percentError = (fR_predicted-fR_actual)./fR_actual*100; absPercentError = abs(percentError); resultsTrain = addvars(dataTrain,fR_predicted,percentError)
resultsTrain=130×10 table
L W l w d h eR fR fR_predicted percentError
__ __ __ ___ __ ___ ____ ____ ____________ ____________
1 30 20 10 5 3 1.6 2.33 3.2 3.1999 -0.0019452
2 35 25 15 7 8 1.6 2.33 2.25 2.2502 0.0074223
4 45 35 25 5 20 1.6 2.33 1.45 1.45 0.00031824
5 50 40 20 10 7 1.6 2.33 1.6 1.6 -0.0030973
6 30 20 20 5 3 1.6 2.33 2.1 2.1 0.001521
8 40 30 30 7.5 5 1.6 2.33 1.35 1.35 -0.0022174
9 45 35 30 5 20 1.6 2.33 1.25 1.2501 0.010948
10 50 40 40 10 7 1.6 2.33 1.85 1.8501 0.0075227
11 30 20 10 10 3 1.6 2.33 3.1 3.1002 0.0058718
12 35 25 15 12 8 1.6 2.33 2.25 2.2503 0.014448
13 40 30 15 15 5 1.6 2.33 2.1 2.1001 0.0025409
14 45 35 25 10 20 1.6 2.33 1.5 1.5003 0.022344
15 50 40 20 20 7 1.6 2.33 1.55 1.55 -0.00071631
16 30 20 20 10 3 1.6 2.33 2 2.0001 0.0026836
17 35 25 25 12 8 1.6 2.33 1.55 1.5502 0.013687
19 45 35 30 10 20 1.6 2.33 1.3 1.3006 0.043943
⋮
Plot the cumulative distribution of the absolute percent error and compute its summary statistics—minimum, maximum, mean, median, and standard deviation.
figure [~,apeStatsTrain] = cdfplot(absPercentError)
apeStatsTrain = struct with fields:
min: 1.1299e-04
max: 0.2406
mean: 0.0160
median: 0.0083
std: 0.0308
xlabel("Absolute Percent Error") ylabel("Proportion of Observations") title("Cumulative Distribution of Prediction Error for Training Data")
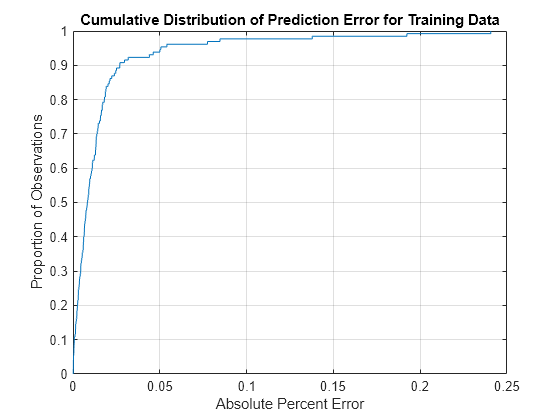
Plot Predicted vs. Actual Responses
Visually compare the predicted responses against the actual responses. If the prediction accuracy is perfect, then all of the points will lie exactly on a diagonal line of slope 1 and intercept 0. The deviation of an observation point from this "perfect prediction line" is the prediction error for the corresponding observation.
figure plot(fR_actual,fR_predicted,"o",DisplayName="Observations") hline = refline(1,0); hline.DisplayName = "Perfect prediction"; idx = find(absPercentError > 5); hold on plot(fR_actual(idx),fR_predicted(idx),"kx",DisplayName="Error > 5%") hold off title("Predictions on Training Data") xlabel("True Response") ylabel("Predicted Response") legend(Location="southeast")
Evaluate Trained Model on Test Data Set
To assess the model's degree of generalization and predictive capability, evaluate it with data that it has not seen, specifically the test data kept aside for this purpose. This helps to gauge the model's ability to make accurate predictions on new observations, which is ultimately the goal of training and tuning the model.
Compute Percent Error in Model Predictions
Use the model's predict function on the test data, and compute the prediction error for each observation.
fR_predicted = predict(mdl,dataTest); fR_actual = dataTest.fR; percentError = (fR_predicted-fR_actual)./fR_actual*100; absPercentError = abs(percentError); resultsTest = addvars(dataTest,fR_predicted,percentError)
resultsTest=30×10 table
L W l w d h eR fR fR_predicted percentError
__ __ __ ___ __ ___ ____ ____ ____________ ____________
3 40 30 15 7.5 5 1.6 2.33 2.5 2.4286 -2.8542
7 35 25 25 7 8 1.6 2.33 1.55 1.5753 1.6335
18 40 30 30 15 5 1.6 2.33 1.3 1.3717 5.5184
24 45 35 25 5 25 1.6 2.33 1.6 1.6146 0.91085
39 45 35 30 10 25 1.6 2.33 2 1.9675 -1.6256
40 50 40 40 20 14 1.6 2.33 1.75 1.792 2.3976
41 30 20 10 5 3 2.5 2.33 3.25 3.1878 -1.9128
44 45 35 25 5 20 2.5 2.33 1.5 1.4658 -2.278
56 30 20 20 10 3 2.5 2.33 2.05 2.0248 -1.2314
58 40 30 30 15 5 2.5 2.33 1.3 1.3812 6.2499
59 45 35 30 10 20 2.5 2.33 1.3 1.3857 6.5904
62 35 25 15 7 10 2.5 2.33 2.25 2.2369 -0.58346
73 40 30 15 15 10 2.5 2.33 2.1 2.1237 1.1295
87 35 25 25 7 8 1.6 4.4 1.9 1.9355 1.8674
98 40 30 30 15 5 1.6 4.4 1.6 1.6424 2.6511
103 40 30 15 7.5 10 1.6 4.4 1.5 1.5456 3.0414
⋮
Plot the cumulative distribution of the absolute percent error, and compute its summary statistics. Note that most of the predictions have less than 5% absolute error.
figure [~,apeStatsTest] = cdfplot(absPercentError)
apeStatsTest = struct with fields:
min: 0.1945
max: 6.5904
mean: 2.3415
median: 1.8085
std: 1.8569
xlabel("Absolute Percent Error") ylabel("Proportion of Observations") title("Cumulative Distribution of Prediction Error for Test Data")
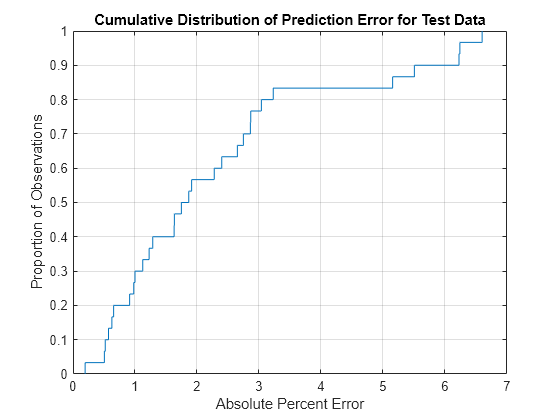
Plot Predicted vs. Actual Responses
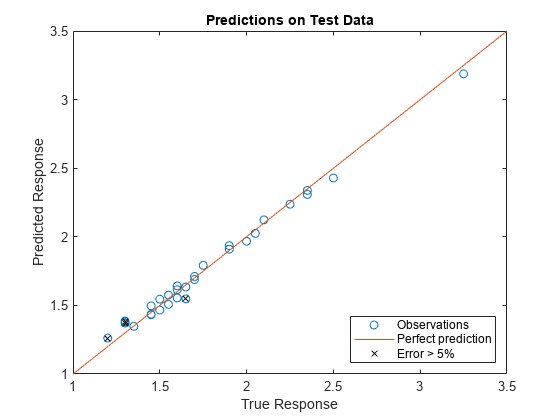
Visually compare the predicted responses against the actual responses. The model performs reasonably well on most of the test data set, but prediction error exceeds 5% for a handful of the observations.
figure plot(fR_actual,fR_predicted,"o",DisplayName="Observations") hline = refline(1,0); hline.DisplayName = "Perfect prediction"; idx = find(absPercentError > 5); hold on plot(fR_actual(idx),fR_predicted(idx),"kx",DisplayName="Error > 5%") hold off title("Predictions on Test Data") xlabel("True Response") ylabel("Predicted Response") legend(Location="southeast")
Conclusion
In this example, you developed a machine learning model to characterize a custom antenna structure based on its key design parameters. Specifically, you trained a regression model to predict the resonant frequency of a C-shaped microstrip patch antenna on a PCB stack. The trained model performed reasonably well on a test data set not previously seen by the model. However, upon comparison to the excellent prediction accuracy on the training data, it appears that the model did overfit to the training data from which it learned. In summary, this model has good predictive power, but indeed there is room for improvement.
Here are some strategies to improve model generalization and combat overfitting. However, a detailed treatment of this topic is outside the scope of this example.
Perform data augmentation, feature engineering, and/or addtional data preprocessing.
Adjust cross-validation options during training and hyperparameter tuning.
Pursue other DOE methods to procure a data set with a more balanced and continuous distribution.
Helper Functions
The following sections define the local, helper functions used in this example to model the antenna and generate response data using full-wave simulation.
Create Model of C-Shaped Microstrip Patch Antenna
The following local function creates a PCB stack model of the C-shaped microstrip patch antenna. This helper function uses custom, 2D shapes and the pcbStack function, and it includes code to visualize the antenna's structure and parameterization. For all parameter sets in this example, the helper function specifies the ground plane dimensions as 1.15 times the respective outer dimensions of the radiating patch.
function ant = createCShapedPatchAntenna(Lmm,Wmm,lmm,wmm,dmm,hmm,eR,feedparams,options) arguments Lmm Wmm lmm wmm dmm hmm eR feedparams options.Visualize (1,1) logical = false end L = Lmm*1e-3; W = Wmm*1e-3; l = lmm*1e-3; w = wmm*1e-3; d = dmm*1e-3; h = hmm*1e-3; GPL = 1.15*L; GPW = 1.15*W; groundplane = antenna.Rectangle(Length=GPL,Width=GPW,Center=[L/2,W/2],Name="Ground Plane"); patch = antenna.Rectangle(Length=L,Width=W,Center=[L/2,W/2]); slot = antenna.Rectangle(Length=l,Width=w,Center=[L-l/2,W-d-w/2]); radiator = patch - slot; radiator.Name = "Radiator"; substrate = dielectric(Name=sprintf("eR = %g",eR),EpsilonR=eR,Thickness=h); x0 = feedparams.x0; y0 = feedparams.y0; V = feedparams.V; ant = pcbStack(BoardShape=groundplane,BoardThickness=h, ... FeedLocations=[x0,y0,1,3],FeedVoltage=V, ... Layers={radiator,substrate,groundplane}); if options.Visualize x0mm = x0*1e3; y0mm = y0*1e3; figure show(ant) view(3) text(Lmm*34/30,0,0,"h",FontName="FixedWidth") text(x0mm-1,y0mm-1,hmm+3,"Feed (x0,y0)",FontName="FixedWidth",HorizontalAlignment="center") figure show(ant) view(2) text(Lmm/2,0,hmm,"L",FontName="FixedWidth",VerticalAlignment="bottom") text(0,Wmm/2,hmm,"W",FontName="FixedWidth") text(Lmm-lmm/2,Wmm-dmm-wmm,hmm,"l",FontName="FixedWidth",VerticalAlignment="bottom") text(Lmm-lmm,Wmm-dmm-wmm/2,hmm,"w",FontName="FixedWidth") text(Lmm,Wmm-dmm/2,hmm,"d",FontName="FixedWidth") end end
Generate Response Data for Observation
The following local function computes the complex-valued S-parameter and impedance responses using full-wave simulation for a given specification of antenna design parameters.
function [S,Z] = generateObservation(T,feedparams,f,options) arguments T feedparams f options.SaveDataToFile (1,1) logical = true options.FileIndex {mustBeInteger,mustBePositive} = 1 options.FolderName {mustBeTextScalar} = "data" end tic ant = createCShapedPatchAntenna( ... T.L, T.W, ... % Outer dimensions T.l, T.w, T.d, ... % Slot dimensions T.h, T.eR, ... % Substrate parameters feedparams); % Feed parameters S = sparameters(ant,f); Z = impedance(ant,f); tElapsed = toc; fprintf("%.2f seconds to generate observation %d.\n",tElapsed,options.FileIndex) if options.SaveDataToFile if ~isfolder(options.FolderName) mkdir(options.FolderName) end filename = fullfile(options.FolderName,sprintf("%.3d.mat",options.FileIndex)); save(filename,"T","feedparams","f","S","Z","tElapsed") end end
References
[1] S. Bhunia, "Effects of Slot Loading on Microstrip Patch Antennas", International Journal of Wired and Wireless Communications, vol. 1, no. 1, pp. 1-6, Oct. 2012.
[2] U. Özkaya, E. Yiğit, L. Seyfi, Ş. Öztürk, and D. Singh, "Comparative Regression Analysis for Estimating Resonant Frequency of C-Like Patch Antennas", Mathematical Problems in Engineering, vol. 2021, pp. 1-8, Feb. 2021.
[3] E. Yigit, "Operating Frequency Estimation of Slot Antenna by Using Adapted kNN Algorithm", International Journal of Intelligent Systems and Applications in Engineering, vol. 6, no. 1, pp. 29-32, Mar. 2018.
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)