Gammatone Filter Bank

Gammatone filter bank

Since R2021b

Libraries:
Audio Toolbox / Filters

Description

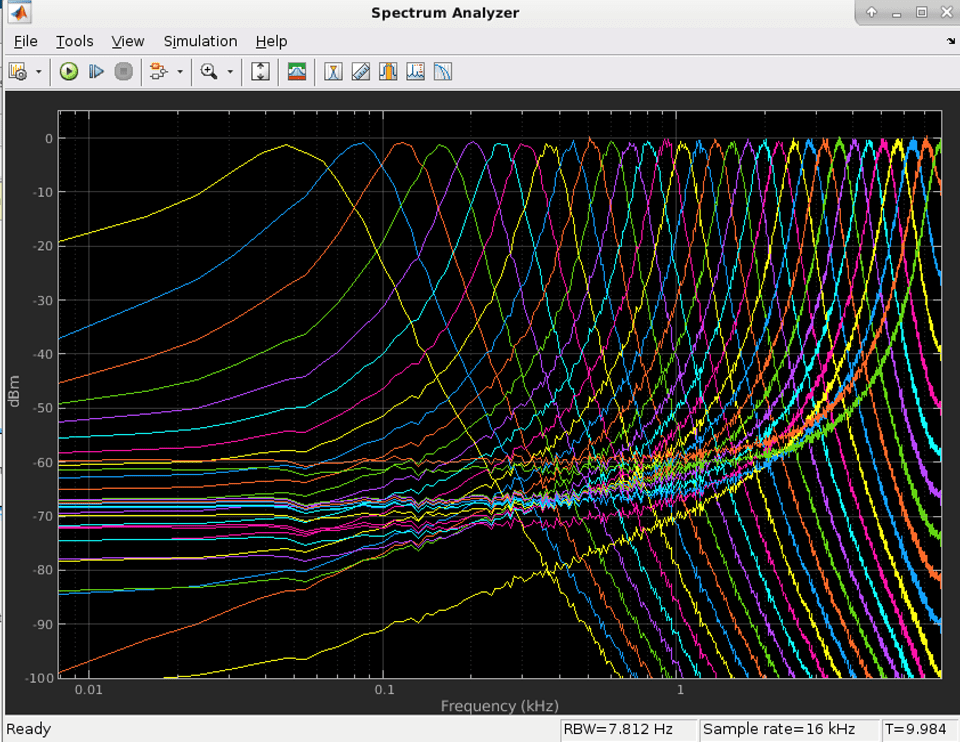
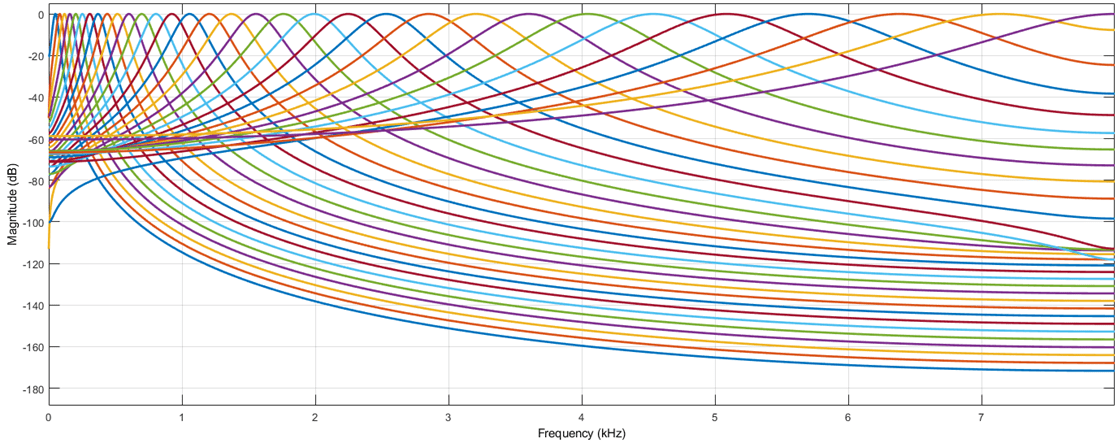
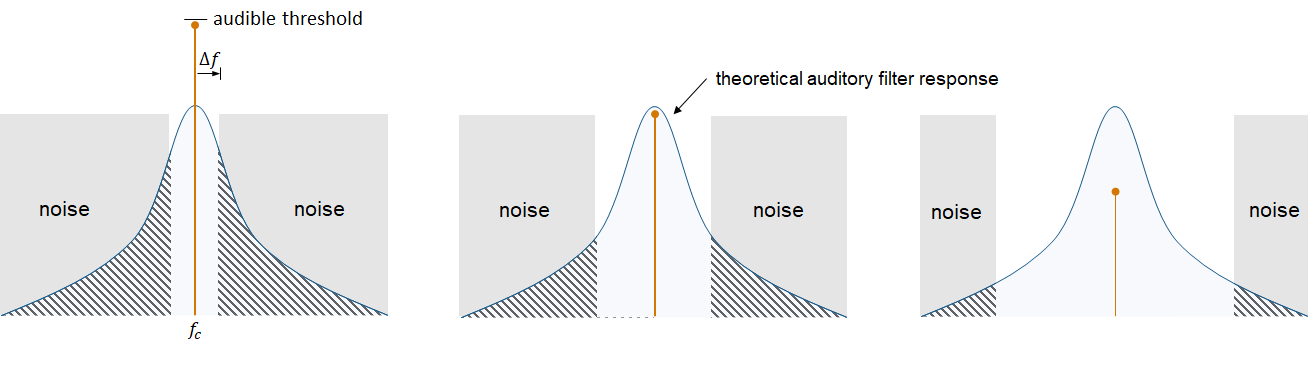
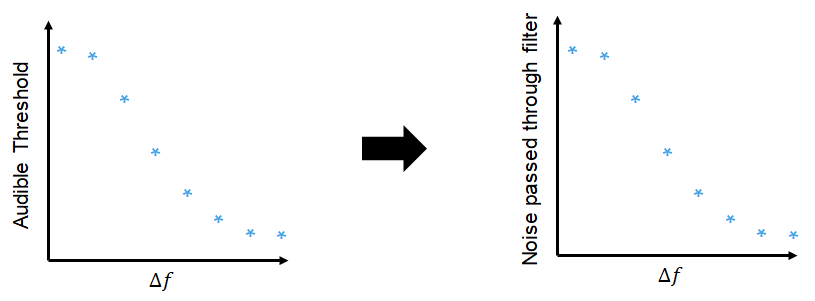
The Gammatone Filter Bank block decomposes a signal by passing it through a bank of gammatone filters equally spaced on the equivalent rectangular bandwidth (ERB) scale. Gammatone filter banks are designed to model the human auditory system.

Examples

Decompose Signal using Gammatone Filter Bank Block

Use the Gammatone Filter Bank block to decompose a signal by passing it through a bank of gammatone filters.

Open Script

Ports

Input

expand all

Port_1 — Audio input to filter bank
scalar | vector | matrix

Audio input to the filter bank, specified as a scalar, vector, or matrix. If you specify the input as a matrix, the block treats the columns as independent audio channels. If you specify the input as a vector, the block treats the input as containing a single channel.

Data Types: single | double

Output

expand all

Port_1 — Audio output from filter bank
scalar | vector | matrix | 3-D array

Audio output from the filter bank, returned as a scalar, vector, matrix, or 3-D array. The shape of output signal depends on the shape of input signal and Number of filters. If input is an M-by-N matrix, then output is an M-by-Number of filters-by-N array. If N is 1, then output is a matrix.

Data Types: single | double

Parameters

expand all

Frequency range (Hz) — Frequency range of filter bank
`[50 8000]` (default) | two-element row vector of monotonically increasing values

Frequency range of the filter bank, specified as a two-element row vector of monotonically increasing values in Hz.

Tunable: No

Number of filters — Number of filters
`32` (default) | positive integer

Number of filters in the filter bank, specified as a positive integer.

Tunable: No

Inherit sample rate from input — Specify sample rate from input port
`off` (default) | `on`

Select this parameter to specify the sample rate from the input port.

Input sample rate (Hz) — Input sample rate
`16000` (default) | positive integer

Input sample rate, specified as a positive integer in Hz.

Tunable: No

Dependencies

To enable this parameter, set Inherit sample rate from input port to off.

Bands as separate output port — Separate ports for each filter output
`off` (default) | `on`

Select this parameter to separate ports for each filter output.

Tunable: No

View Filter Response — Visualize filter bank responses
button

This button visualizes gammatone filter bank responses.

Variable name — Variable name of exported filter bank
`myFilt` (default) | valid variable name

Name of the variable in the base workspace to contain the filter bank when it is exported. The name must be a valid MATLAB^® variable name.

Overwrite variable if it already exists — Overwrite variable if it already exists
`on` (default) | `off`

When you select this parameter, exporting the filter bank overwrites the variable specified by the Variable name parameter if it already exists in the base workspace. If you do not select this parameter and the specified variable already exists in the workspace, exporting the filter bank creates a new variable with an underscore and a number appended to the variable name. For example, if the variable name is var and it already exists, the exported variable will be named var_1.

Export filter to workspace — Export filter bank to workspace
button

Export the filter bank to the base workspace in the variable specified by the Variable name parameter.

Tips

You cannot export the filter if you have enabled the Inherit sample rate from input parameter and the model is not running.

Simulate using — Specify type of simulation to run
`Interpreted execution` (default) | `Code generation`

Type of simulation to run, specified as one of the following:

Interpreted execution –– Simulate model using the MATLAB interpreter. This option shortens startup time and has simulation speed comparable to Code generation. In this mode, you can debug the source code of the block.
Code generation –– Simulate model using generated C code. The first time you run a simulation, Simulink^® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but the speed of the subsequent simulations is faster than Interpreted execution.

Tunable: No

Block Characteristics

Data Types	`double` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`no`
Variable-Size Signals	`yes`
Zero-Crossing Detection	`no`

Algorithms

expand all

Applications

A gammatone filter bank is often used as the front end of a cochlea simulation. A cochlea simulation transforms complex sounds into a multichannel activity pattern like the one observed in the auditory nerve [2].The Gammatone Filter Bank block follows the algorithm described in [1]. The algorithm is an implementation of an idea proposed in [2]. The design of the gammatone filter bank can be described in two parts: the filter shape (gammatone) and the frequency scale. The equivalent rectangular bandwidth (ERB) scale defines the relative spacing and bandwidth of the gammatone filters. The derivation of the ERB scale also provides an estimate of the auditory filter response that closely resembles the gammatone filter.

Frequency Scale

The block determines the ERB scale using the notched-noise masking method. This method involves a listening test wherein notched noise is centered on a tone. The power of the tone is tuned, and the audible threshold (the power required for the tone to be heard) is recorded. The experiment is repeated for different notch widths and center frequencies.

The notched-noise method assumes that the audible threshold corresponds to a constant signal-to-masker ratio at the output of the theoretical auditory filter. That is, the ratio of the power of the f_c tone and the shaded area is constant. Therefore, the relationship between the audible threshold and 2Δf (the notch bandwidth) is linearly related to the relationship between the noise passed through the filter and 2Δf.

The derivative of the function relating Δf to the noise passed through the filter estimates the shape of the auditory filter. Because Δf has an inverse relationship with the noise power passed through the filter, the derivative of the function must be multiplied by –1. The resulting shape of the auditory filter is usually approximated as a roex filter.

The equivalent rectangular bandwidth of the auditory filter is defined as the width of a rectangular filter required to pass the same noise power as the auditory filter.

[4] defines ERB as a function of center frequency for young listeners with normal hearing and a moderate noise level:

$ERB = 24.7 (0.00437 f_{c} + 1)$

The ERB scale (ERBs) is an extension of the relationship between ERB and the center frequency, derived by integrating the reciprocal of the ERB function:

$ERBs = 21.4 \log_{10} (0.00437 f + 1)$

To design a gammatone filter bank, [2] suggests distributing the center frequencies of the filters in proportion to their bandwidth. To accomplish this, Gammatone Filter Bank block defines the center frequencies as linearly spaced on the ERB scale, covering the specified frequency range with the desired number of filters. You can specify the frequency range and desired number of filters using the Frequency range (Hz) and Number of filters parameters.

Gammatone Filter

The gammatone filter was introduced in [3]. The continuous impulse response is:

$g (t) = a t^{n - 1} e^{- 2 π b t} \cos (2 π f_{c} t + ϕ)$

where

a –– amplitude factor
t –– time in seconds
n –– filter order (set to four to model human hearing)
f_c–– center frequency
b –– bandwidth, set to 1.019*hz2erb(f_c).
ϕ –– phase factor

The gammatone filter is similar to the roex filter derived from the notched-noise experiment. The Gammatone Filter Bank block implements the digital filter as a cascade of four second-order sections, as described in [1].

References

[1] Slaney, Malcolm. "An Efficient Implementation of the Patterson-Holdsworth Auditory Filter Bank." Apple Computer Technical Report 35, 1993.

[2] Patterson, R.D., K. Robinson, J. Holdsworth, D. McKeown, C. Zhang, and M. Allerhand. "Complex Sounds and Auditory Images." Auditory Physiology and Perception. 1992, pp. 429–446.

[3] Aertsen, A. M. H. J., and P. I. M. Johannesma. "Spectro-Temporal Receptive Fields of Auditory Neurons in the Grassfrog." Biological Cybernetics. Vol. 38, Issue 4, 1980, pp. 223–234.

[4] Glasberg, Brian R., and Brian C. J. Moore. "Derivation of Auditory Filter Shapes from Notched-Noise Data." Hearing Research. Vol. 47. Issue 1-2, 1990, pp. 103–138.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2021b

Gammatone Filter Bank

Description

Examples

Decompose Signal using Gammatone Filter Bank Block

Ports

Input

Port_1 — Audio input to filter bank scalar | vector | matrix

Output

Port_1 — Audio output from filter bank scalar | vector | matrix | 3-D array

Parameters

Frequency range (Hz) — Frequency range of filter bank [50 8000] (default) | two-element row vector of monotonically increasing values

Number of filters — Number of filters 32 (default) | positive integer

Inherit sample rate from input — Specify sample rate from input port off (default) | on

Input sample rate (Hz) — Input sample rate 16000 (default) | positive integer

Dependencies

Bands as separate output port — Separate ports for each filter output off (default) | on

View Filter Response — Visualize filter bank responses button

Variable name — Variable name of exported filter bank myFilt (default) | valid variable name

Overwrite variable if it already exists — Overwrite variable if it already exists on (default) | off

Export filter to workspace — Export filter bank to workspace button

Tips

Simulate using — Specify type of simulation to run Interpreted execution (default) | Code generation

Block Characteristics

Algorithms

Applications

Frequency Scale

Gammatone Filter

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Port_1 — Audio input to filter bank
scalar | vector | matrix

Port_1 — Audio output from filter bank
scalar | vector | matrix | 3-D array

Frequency range (Hz) — Frequency range of filter bank
`[50 8000]` (default) | two-element row vector of monotonically increasing values

Number of filters — Number of filters
`32` (default) | positive integer

Inherit sample rate from input — Specify sample rate from input port
`off` (default) | `on`

Input sample rate (Hz) — Input sample rate
`16000` (default) | positive integer

Bands as separate output port — Separate ports for each filter output
`off` (default) | `on`

View Filter Response — Visualize filter bank responses
button

Variable name — Variable name of exported filter bank
`myFilt` (default) | valid variable name

Overwrite variable if it already exists — Overwrite variable if it already exists
`on` (default) | `off`

Export filter to workspace — Export filter bank to workspace
button

Simulate using — Specify type of simulation to run
`Interpreted execution` (default) | `Code generation`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.