Bit Error Rate Analysis

Analyze BER performance of communications systems

Description

The Bit Error Rate Analysis app calculates the bit error rate (BER) as a function of the energy per bit to noise power spectral density ratio (E_b/N₀). Using this app, you can:

Generate BER data for a communications system and analyze performance using:
- Monte Carlo simulations of MATLAB^® functions and Simulink^® models.
- Theoretical closed-form expressions for selected types of communications systems.
- Run systems contained in MATLAB simulation functions or Simulink models. After you create a function or model that simulates the system, the Bit Error Rate Analysis app iterates over your choice of E_b/N₀ values and collects the results.
Plot one or more BER data sets on a single set of axes. You can graphically compare simulation data with theoretical results or simulation data from a series of communications system models.
Fit a curve to a set of simulation data.
Plot confidence levels of simulation data.
Send BER data to the MATLAB workspace or to a file for further processing.

For more information, see Analyze Performance with Bit Error Rate Analysis App.

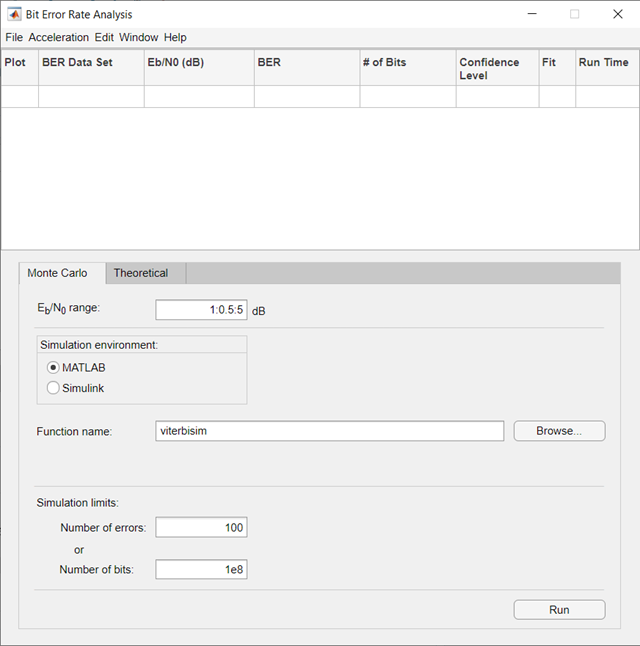
Open the Bit Error Rate Analysis App

MATLAB Toolstrip: On the Apps tab, under Signal Processing and Communications, click the app icon.
MATLAB command prompt: Enter bertool.

Examples

expand all

Compute BER Using Theoretical Tab

Generate a theoretical estimate of BER performance for a 16-QAM link in AWGN.

Open the Bit Error Rate Analysis app.

bertool

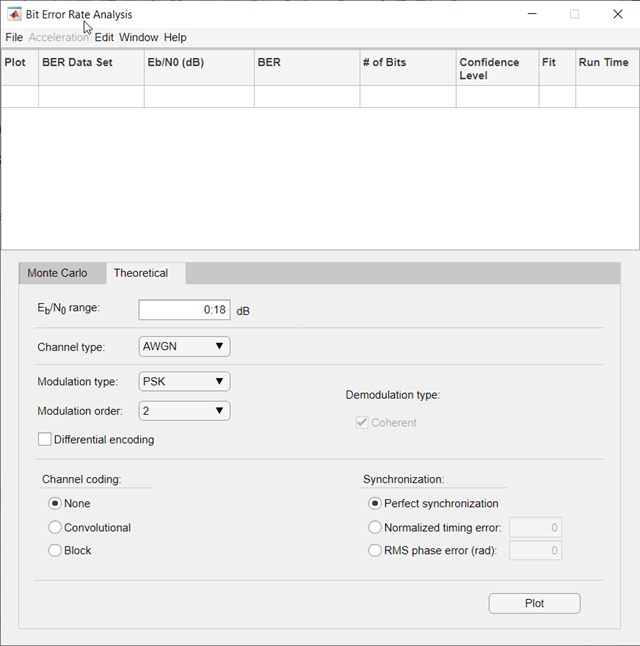
BER Analysis app mask

On the Theoretical tab, set these parameters to the specified values: E_b/N₀ range to 0:10, Modulation type to QAM, and Modulation order to 16.

Plot the BER curve by clicking Plot.

Compute BER Using Monte Carlo Tab and MATLAB Function Simulation

Simulate the BER by using a custom MATLAB function. By default, the app uses the viterbisim.m simulation.

Open the Bit Error Rate Analysis app.

bertool

On the Monte Carlo tab, set the E_b/N₀ range parameter to 1:.5:6. Run the simulation and plot the estimated BER values by clicking Run.

On the Theoretical tab, set E_b/N₀ range to 1:6 and set Modulation order to 4. Enable convolutional coding by selecting Convolutional. Click Plot to add the theoretical upper bound of the BER curve to the plot.

Prepare MATLAB Function for Use in Bit Error Rate Analysis App

Add code to the simulation function template given in the Template for Simulation Function topic to run in the Monte Carlo tab of the Bit Error Rate Analysis.

Prepare Function

Copy the template from the Template for Simulation Function topic into a new MATLAB file in the MATLAB Editor. Save the file in a folder on your MATLAB path, using the file name bertool_simfcn.

Place lines of code that initialize parameters or create objects used in the simulation in the template section marked Set up initial parameters. This code maps simulation variables to the template input arguments. For example, snr maps to EbNo.

% Set up initial parameters.
siglen = 1000; % Number of bits in each trial
M = 2;         % DBPSK is binary
snr = EbNo;    % Because of binary modulation

% Create an ErrorRate calculator System object to compare 
% decoded symbols to the original transmitted symbols.
errorCalc = comm.ErrorRate;

Place the code for the core simulation tasks in the template section marked Proceed with simulation. This code includes the core simulation tasks, after all setup work has been performed.

    msg = randi([0,M-1],siglen,1); % Generate message sequence
    txsig = dpskmod(msg,M);        % Modulate
    hChan.SignalPower = ...        % Calculate and assign signal power
        (txsig'*txsig)/length(txsig); 
    rxsig = awgn(txsig,snr,'measured'); % Add noise
    decodmsg = dpskdemod(rxsig,M);      % Demodulate
    berVec = errorCalc(msg,decodmsg);   % Calculate BER
    totErr = totErr + berVec(2);
    numBits = numBits + berVec(3);

After you insert these two code sections into the template, the bertool_simfcn function is compatible with the Bit Error Rate Analysis app. The resulting code resembles this code segment.

function [ber,numBits] = bertool_simfcn(EbNo,maxNumErrs,maxNumBits,varargin)
%
%   See also BERTOOL and VITERBISIM.

% Copyright 2020 The MathWorks, Inc.

% Initialize variables related to exit criteria.
totErr = 0;  % Number of errors observed
numBits = 0; % Number of bits processed

% --- Set up the simulation parameters. ---
% --- INSERT YOUR CODE HERE.
% Set up initial parameters.
siglen = 1000; % Number of bits in each trial
M = 2;         % DBPSK is binary.
snr = EbNo;    % Because of binary modulation
% Create an ErrorRate calculator System object to compare
% decoded symbols to the original transmitted symbols.
errorCalc = comm.ErrorRate;

% Simulate until the number of errors exceeds maxNumErrs
% or the number of bits processed exceeds maxNumBits.
while((totErr < maxNumErrs) && (numBits < maxNumBits))

    % Check if the user clicked the Stop button of BERTool.
    if isBERToolSimulationStopped(varargin{:})
      break
    end
  
    % --- Proceed with the simulation.
    % --- Update totErr and numBits.
    % --- INSERT YOUR CODE HERE.
    msg = randi([0,M-1],siglen,1); % Generate message sequence
    txsig = dpskmod(msg,M);        % Modulate
    hChan.SignalPower = ...        % Calculate and assign signal power
        (txsig'*txsig)/length(txsig); 
    rxsig = awgn(txsig,snr,'measured'); % Add noise
    decodmsg = dpskdemod(rxsig,M);      % Demodulate
    berVec = errorCalc(msg,decodmsg);   % Calculate BER
    totErr = totErr + berVec(2);
    numBits = numBits + berVec(3);
end % End of loop

% Compute the BER.
ber = totErr/numBits;

The function has inputs to specify the app and scalar quantities for EbNo, maxNumErrs, and maxNumBits that are provided by the app. The Bit Error Rate Analysis app is an input because the function monitors and responds to the stop command in the app. The bertool_simfcn function excludes code related to plotting, curve fitting, and confidence intervals because the Bit Error Rate Analysis app enables you to do similar tasks interactively without writing code.

Use Prepared Function

Run bertool_simfcn in the Bit Error Rate Analysis app.

Open the Bit Error Rate Analysis app, and then select the Monte Carlo tab.

Set these parameters to the specified values: E_b/N₀ range to 0:10, Simulation environment to MATLAB, Function name to bertool_simfcn, Number of errors to 5, and Number of bits to 1e8.

Parameter settings on the Monte Carlo tab of the Bit Error Rate Analysis app.

Click Run.

The Bit Error Rate Analysis app computes the results and then plots them. In this case, the results do not appear to fall along a smooth curve because the simulation required only five errors for each value in EbNo.

DBPSK modulation BER plot generated with number of errors set to five.

Fit a curve to the series of points in the BER Figure window, by selecting the Fit parameter in the data viewer.

Data set listed in the data viewer pane of the Bit Error Rate Analysis app

The Bit Error Rate Analysis app plots the fitted curve, as shown in this figure.

DBPSK modulation BER plot with fitted curve.

Compute Error Rate Simulation Sweeps Using Bit Error Rate Analysis App

Open Live Script

Use the Bit Error Rate Analysis app to compute the BER as a function of $E_{b} / N_{0}$ . The app analyzes performance with either Monte Carlo simulations of MATLAB® functions and Simulink® models or theoretical closed-form expressions for selected types of communications systems. The code in the mpsksim.m function provides an M-PSK simulation that you can run from the Monte Carlo tab of the app.

Open the Bit Error Rate Analysis app from the Apps tab or by running the bertool function in the MATLAB command window.

On the Monte Carlo tab, set the $E_{b} / N_{0}$ range parameter to 1:1:5 and the Function name parameter to mpsksim.

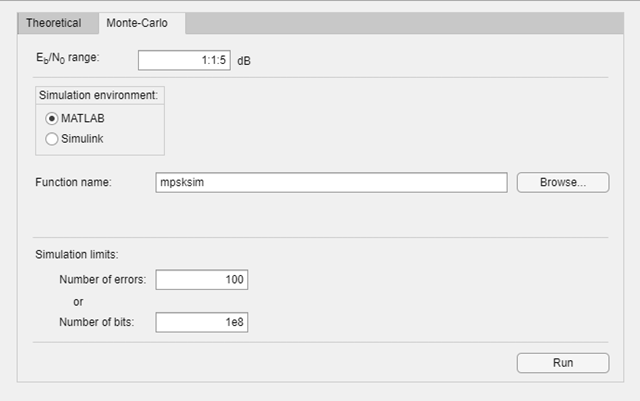
Open the mpsksim function for editing, set M=2, and save the changed file.

Run the mpsksim.m function as configured by clicking Run on the Monte Carlo tab in the app.

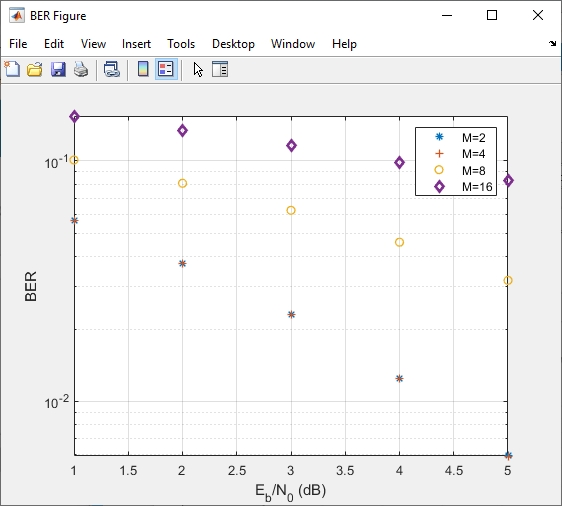
After the app simulates the set of $E_{b} / N_{0}$ points, update the name of the BER data set results by selecting simulation0 in the BER Data Set field and typing M=2 to rename the set of results. The legend on the BER figure updates the label to M=2.

Update the value for M in the mpsksim function, repeating this process for M = 4, 8, and 16. For example, these figures of the Bit Error Rate Analysis app and BER Figure window show results for varying M values.

Parallel SNR Sweep Using Bit Error Rate Analysis App

The default configuration for the Monte Carlo processing of the Bit Error Rate Analysis app automatically uses parallel pool processing to process individual $E_{b} / N_{0}$ points when you have the Parallel Computing Toolbox™ software but for the processing of your simulation code:

Any parfor function loops in your simulation code execute as standard for loops.
Any parfeval (Parallel Computing Toolbox) function calls in your simulation code execute serially.
Any spmd (Parallel Computing Toolbox) statement calls in your simulation code execute serially.

Prepare Simulink Model for Use with Bit Error Rate Analysis App

This example uses:

Open Live Script

This example shows you how to use a Simulink® model to run in the Monte Carlo tab of the Bit Error Rate Analysis app and compare the BER performance of the Simulink® simulation results with theoretical BER results.

Prepare Model and App

Open the example to load the doc_bpsk model into a working folder on your computer.

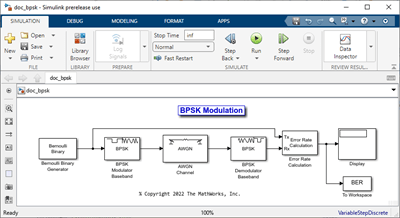
Simulink model of BPSK modulation simulation

Open the doc_bpsk model from the working directory it was downloaded to and the Bit Error Rate Analysis app from the apps gallery. Parameters that control the $E_{b} / N_{0}$ range, load the model, save the results, and set the stopping criteria for each BER iteration must align in the Bit Error Rate Analysis app and in the Simulink® model.

On the Monte Carlo tab in the app,

The $E_{b} / N_{0}$ range parameter maps to the variable name EbNo.
The Number of errors parameter maps to the variable name maxNumErrs.
The Number of bits parameter maps to the variable name maxNumBits.
Select Simulink for the Simulation environment. For Model name enter doc_bspk and for BER variable name enter BER.

In the model, the PreloadFcn callback function initializes variables for EbNo, maxNumErrs, and maxNumBits that set block parameters in the model. For more information on the PreloadFcn callback function, see Model Callbacks (Simulink). To ensure the app will control the model, in the model confirm that the:

AWGN Channel block has Es/No (dB) set to EbNo. For BPSK modulation, $E_{s} / N_{0}$ is equivalent to $E_{b} / N_{0}$ .
Error Rate Calculation block has Target number of errors set to maxNumErrs, and Maximum number of symbols set to maxNumBits.
To Workspace block has Variable name set to BER.
In the model Simulation, set Stop Time to Inf.

Use Prepared Model

In the Monte Carlo tab of the Bit Error Rate Analysis app, set:

$E_{b} / N_{0}$ range to 0:9
Number of errors to 100
Number of bits to 1e8

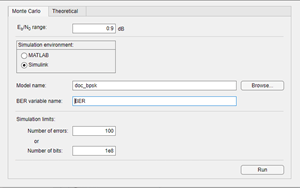
Parameter settings on the Monte Carlo tab of the Bit Error Rate Analysis app

Click Run. The Bit Error Rate Analysis app computes the results and then plots them.

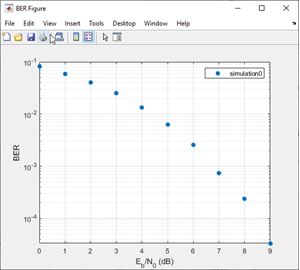
BER figure of BSPK modulation

Compare these simulation results with the theoretical results, by clicking the Theoretical tab in the app and setting Eb/N0 range to 0:9.

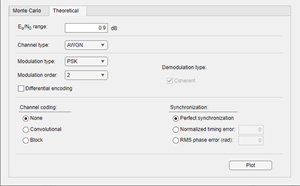
Theoretical tab on Bit Error Rate Analysis app configured for BPSK modulation

Click Plot.

The app plots the theoretical curve in the BER Figure window along with the earlier simulation results.

BER figure of BSPK modulation with theoretical results curve

Parameters

expand all

Theoretical

`E_b/N₀ range` — Range of E_b/N₀ values
`0:18` (default) | scalar | vector

Range of E_b/N₀ values over which the BER is evaluated, specified as a scalar or vector. Units are in dB.

Example: 5:10 specifies the evaluation of E_b/N₀ values over the range [5, 10] at 1 dB increments.

`Channel type` — Type of channel over which BER is evaluated
`AWGN` (default) | `Rayleigh` | `Rician`

Type of channel over which the BER is evaluated, specified as AWGN, Rayleigh, or Rician. The Rayleigh and Rician options correspond to flat fading channels.

`Modulation type` — Modulation type of communications link
`PSK` (default) | `DPSK` | `OQPSK` | `PAM` | `QAM` | `FSK` | `MSK` | `CPFSK`

Modulation type of the communications link, specified as PSK, DPSK, OQPSK, PAM, QAM, FSK, MSK, or CPFSK.

`Modulation order` — Modulation order of communications link
`2` (default) | `4` | `8` | `16` | `32` | `64`

Modulation order of the communications link, specified as 2, 4, 8, 16, 32, or 64.

`Differential encoding` — Differential encoding of input data
`off` (default) | `on`

Select this parameter to enable differential encoding of the input data.

`Correlation coefficient` — Correlation coefficient
`0` (default) | real scalar in the range [-1, 1]

Correlation coefficient, specified as a real scalar in the range [-1, 1].

Dependencies

To enable this parameter, set Modulation type to FSK.

`Modulation index` — Modulation index
`0.5` (default) | positive real scalar

Modulation index, specified as a positive real scalar.

Dependencies

To enable this parameter, set Modulation type to CPFSK.

`Demodulation type` — Coherent demodulation of input data
`on` (default) | `off`

Select this parameter to enable coherent demodulation of the input data.
Clear this parameter to enable noncoherent demodulation of the input data.

Dependencies

To enable this parameter, set Modulation type to FSK or MSK.

`Channel coding` — Channel coding type used when estimating theoretical BER
None (default) | Convolutional | Block

Channel coding type used when estimating the theoretical BER, specified as None, Convolutional, or Block.

`Synchronization` — Synchronization error
Perfect synchronization (default) | Normalized timing error | RMS phase noise level

Synchronization error in the demodulation process, specified as Perfect synchronization, Normalized timing error, or RMS phase noise (rad).

When you set Synchronization to Perfect synchronization no synchronization errors are encountered in the demodulation process.
When you set Synchronization to Normalized timing error, you can set the normalized timing error as a scalar in the range [0, 0.5].
When you set Synchronization to RMS phase noise (rad), you can set the RMS phase noise level as a nonnegative scalar. Units are in radians

Dependencies

To enable this parameter, set Modulation type to PSK, Modulation order to 2, and Channel coding to None.

`Decision method` — Decoding decision method
`Hard` (default) | `Soft`

Decoding decision method used to decode the received data, specified as Hard or Soft.

Dependencies

To enable this parameter, set Channel coding to Convolutional or set Channel coding to Block and set Coding type to General.

`Trellis` — Convolutional code trellis
`poly2trellis(7,[171 133])` (default) | structure

Convolutional code trellis, specified as a structure variable. You can generate this structure by using the poly2trellis function.

Dependencies

To enable this parameter, set Channel coding to Convolutional.

`Coding type` — Block coding type
`General` (default) | `Hamming` | `Golay` | `Reed-Solomon`

Block coding type used in the BER evaluation, specified as General, Hamming, Golay, or Reed-Solomon.

Dependencies

To enable this parameter, set Channel coding to Block.

`N` — Codeword length
positive integer

Codeword length, specified as a positive integer.

Dependencies

To enable this parameter, set Channel coding to Block and set Coding type to General.

`K` — Message length
positive integer

Message length, specified as a positive integer such that K is less than N.

Dependencies

To enable this parameter, set Channel coding to Block and set Coding type to General.

`d_min` — Minimum distance of (N,K) block code
positive integer

Minimum distance of the (N,K) block code, specified as a positive integer.

Dependencies

To enable this parameter, set Channel coding to Block and set Coding type to General.

Monte Carlo

`E_b/N₀ range` — Range of E_b/N₀ values
`1:0.5:5` (default) | scalar | vector

Range of E_b/N₀ values over which the BER is evaluated, specified as a scalar or vector. Units are in dB.

Example: 4:2:10 specifies evaluation of E_b/N₀ over the range [4, 10] at 2 dB increments.

`Simulation environment` — Simulation environment
MATLAB (default) | Simulink

Simulation environment, specified as MATLAB or Simulink.

`Function name` — Name of MATLAB function
`viterbisim` (default)

Name of the MATLAB function for the app to run for the Monte Carlo simulation.

Dependencies

To enable this parameter, set Simulation environment to MATLAB.

`Model name` — Name of Simulink model
`commgraycode` (default)

Name of the Simulink model for the app to run for the Monte Carlo simulation.

Dependencies

To enable this parameter, set Simulation environment to Simulink.

`BER variable name` — Name of variable containing BER simulation data
`grayBER` (default)

Name of the variable containing the BER simulation data. To output the BER simulation data to the MATLAB workspace, you can assign this variable name as the Variable name parameter value in a To Workspace block.

Tip

Select the To Workspace block from the DSP System Toolbox™ / Sinks sublibrary. For more information, see To Workspace Block Configuration for Communications System Simulations.

Dependencies

To enable this parameter, set the Simulation environment to Simulink.

`Number of errors` — Number of errors to be measured before simulation stops
`100` (default) | positive integer

Number of errors to be measured before the simulation stops, specified as a positive integer. Typically, to produce an accurate BER estimate,100 measured errors are enough.

`Number of bits` — Number of bits to be processed before simulation stops
`1e8` (default) | positive integer

Number of bits to be processed before the simulation stops, specified as a positive integer. This parameter is used to prevent the simulation from running too long.

Note

The Monte Carlo simulation stops when either the number of errors or number of bits threshold is reached.

Tips

You can stop the simulation by clicking Stop on the Monte Carlo Simulation dialog box.

Version History

Introduced before R2006a

expand all

R2020b: Semianalytic tab in the Bit Error Rate Analysis has been removed

The Semianalytic tab and functionality in the Bit Error Rate Analysis app has been removed. To generate semianalytic BER results, you can still use the semianalytic function.

For example, this code shows you how to use the semianalytic function to programmatically generate semianalytic BER results for a BPSK-modulated signal.

data = [0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 0].';
bpskmod = comm.BPSKModulator
txSig = rectpulse(bpskmod(data),16); 
rxSig = rectpulse(bpskmod(data),16); % Before receive filter 
modType = ‘psk’; 
modOrder = 2; 
sps = 16; % samples per symbol
num = ones(16,1) / 16; % Filter numerator 
den = 1 % Filter denominator 
EbNo = 0:18; % dB 
BER = semianalytic(txSig,rxSig,modType,modOrder,sps,num,den,EbNo); 
semilogy(EbNo,BER)

Bit Error Rate Analysis

Description

Open the Bit Error Rate Analysis App

Examples

Compute BER Using Theoretical Tab

Compute BER Using Monte Carlo Tab and MATLAB Function Simulation

Prepare MATLAB Function for Use in Bit Error Rate Analysis App

Compute Error Rate Simulation Sweeps Using Bit Error Rate Analysis App

Prepare Simulink Model for Use with Bit Error Rate Analysis App

Parameters

Eb/N0 range — Range of Eb/N0 values 0:18 (default) | scalar | vector

Channel type — Type of channel over which BER is evaluated AWGN (default) | Rayleigh | Rician

Modulation type — Modulation type of communications link PSK (default) | DPSK | OQPSK | PAM | QAM | FSK | MSK | CPFSK

Modulation order — Modulation order of communications link 2 (default) | 4 | 8 | 16 | 32 | 64

Differential encoding — Differential encoding of input data off (default) | on

Correlation coefficient — Correlation coefficient 0 (default) | real scalar in the range [-1, 1]

Dependencies

Modulation index — Modulation index 0.5 (default) | positive real scalar

Dependencies

Demodulation type — Coherent demodulation of input data on (default) | off

Dependencies

Channel coding — Channel coding type used when estimating theoretical BER None (default) | Convolutional | Block

Synchronization — Synchronization error Perfect synchronization (default) | Normalized timing error | RMS phase noise level

Dependencies

Decision method — Decoding decision method Hard (default) | Soft

Dependencies

Trellis — Convolutional code trellis poly2trellis(7,[171 133]) (default) | structure

Dependencies

Coding type — Block coding type General (default) | Hamming | Golay | Reed-Solomon

Dependencies

N — Codeword length positive integer

Dependencies

K — Message length positive integer

Dependencies

dmin — Minimum distance of (N,K) block code positive integer

Dependencies

Eb/N0 range — Range of Eb/N0 values 1:0.5:5 (default) | scalar | vector

Simulation environment — Simulation environment MATLAB (default) | Simulink

Function name — Name of MATLAB function viterbisim (default)

Dependencies

Model name — Name of Simulink model commgraycode (default)

Dependencies

BER variable name — Name of variable containing BER simulation data grayBER (default)

Dependencies

Number of errors — Number of errors to be measured before simulation stops 100 (default) | positive integer

Number of bits — Number of bits to be processed before simulation stops 1e8 (default) | positive integer

Tips

Version History

R2020b: Semianalytic tab in the Bit Error Rate Analysis has been removed

See Also

Functions

Topics

`E_b/N₀ range` — Range of E_b/N₀ values
`0:18` (default) | scalar | vector

`Channel type` — Type of channel over which BER is evaluated
`AWGN` (default) | `Rayleigh` | `Rician`

`Modulation type` — Modulation type of communications link
`PSK` (default) | `DPSK` | `OQPSK` | `PAM` | `QAM` | `FSK` | `MSK` | `CPFSK`

`Modulation order` — Modulation order of communications link
`2` (default) | `4` | `8` | `16` | `32` | `64`

`Differential encoding` — Differential encoding of input data
`off` (default) | `on`

`Correlation coefficient` — Correlation coefficient
`0` (default) | real scalar in the range [-1, 1]

`Modulation index` — Modulation index
`0.5` (default) | positive real scalar

`Demodulation type` — Coherent demodulation of input data
`on` (default) | `off`

`Channel coding` — Channel coding type used when estimating theoretical BER
None (default) | Convolutional | Block

`Synchronization` — Synchronization error
Perfect synchronization (default) | Normalized timing error | RMS phase noise level

`Decision method` — Decoding decision method
`Hard` (default) | `Soft`

`Trellis` — Convolutional code trellis
`poly2trellis(7,[171 133])` (default) | structure

`Coding type` — Block coding type
`General` (default) | `Hamming` | `Golay` | `Reed-Solomon`

`N` — Codeword length
positive integer

`K` — Message length
positive integer

`d_min` — Minimum distance of (N,K) block code
positive integer

`E_b/N₀ range` — Range of E_b/N₀ values
`1:0.5:5` (default) | scalar | vector

`Simulation environment` — Simulation environment
MATLAB (default) | Simulink

`Function name` — Name of MATLAB function
`viterbisim` (default)

`Model name` — Name of Simulink model
`commgraycode` (default)

`BER variable name` — Name of variable containing BER simulation data
`grayBER` (default)

`Number of errors` — Number of errors to be measured before simulation stops
`100` (default) | positive integer

`Number of bits` — Number of bits to be processed before simulation stops
`1e8` (default) | positive integer