Main Content

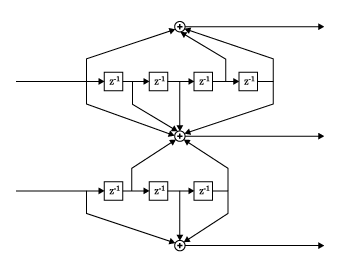
distspec

Compute distance spectrum of convolutional code

collapse all in page

Syntax

spect = distspec(trellis,numcomp)

Description

spect = distspec(trellis,numcomp) computes the free distance and the requested number of components of the weight and distance spectra of a linear convolutional code. Because convolutional codes do not have block boundaries, the weight spectrum and distance spectrum are semi-infinite and well approximated by the first few components.

example

Examples

collapse all

Open Live Script

Use the distspec function to compute the distance spectrum for a rate 2/3 convolutional code. Use the output distance spectrum as an input to the bercoding function, to find a theoretical upper bound on the bit error rate for a system that uses this code with coherent BPSK modulation. Plot the upper bound using the berfit function.

The diagram shows a rate 2/3 encoder with two input streams, three output streams, and two shift registers.

Create a trellis structure to represent the encoder. Set the constraint length of the upper path to 5 and the constraint length of the lower path to 4. The octal representation of the code generator matrix corresponds to the taps from the upper and lower shift registers. The trellis structure serves as an input to the distspec function to represent the rate 2/3 convolutional code.

trellis = poly2trellis([5 4],[23 35 0; 0 5 13])
trellis = struct with fields:
     numInputSymbols: 4
    numOutputSymbols: 8
           numStates: 128
          nextStates: [128x4 double]
             outputs: [128x4 double]


spect = distspec(trellis,4)
spect = struct with fields:
     dfree: 5
    weight: [1 6 28 142]
     event: [1 2 8 25]

Use the bercoding function and the distance spectrum structure to find a theoretical upper bound on the bit error rate for a system that uses this code with coherent BPSK modulation. Plot the upper bound using the berfit function.

berub = bercoding(1:10,'conv','hard',2/3,spect);  % BER upper bound
berfit(1:10,berub); ylabel('Upper Bound on BER'); % Plot

Figure contains an axes object. The axes object with title BER vs. Eb/No with Best Curve Fit, xlabel Eb/No (dB), ylabel Upper Bound on BER contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Empirical BER, Exp Fit.

Input Arguments

collapse all

Trellis description, specified as a MATLAB® structure that contains the trellis description for a rate K/N code. K represents the number of input bit streams, and N represents the number of output bit streams.

The trellis structure contains these fields. You can either use the poly2trellis function to create the trellis structure or create it manually. For more about this structure, see Trellis Description of a Convolutional Code and the istrellis function.

Number of symbols input to the encoder, specified as an integer equal to 2K, where K is the number of input bit streams.

Number of symbols output from the encoder, specified as an integer equal to 2N, where N is the number of output bit streams.

Number of states in the encoder, specified as a power of 2.

Next states for all combinations of current states and current inputs, specified as a matrix of integers. The matrix size must be numStates by 2K.

Outputs for all combinations of current states and current inputs, specified as a matrix of octal numbers. The matrix size must be numStates by 2K.

Data Types: struct

Requested number of components of the weight and distance spectra of a linear convolutional code to compute, specified as a positive integer

Data Types: double

Output Arguments

collapse all

Distance spectrum, returned as a structure containing these fields:

FieldMeaning
spect.dfreeFree distance of the code. This is the minimum number of errors in the encoded sequence required to create an error event.
spect.weightA length-n vector that lists the total number of information bit errors in the error events enumerated in spect.event.
spect.eventA length-n vector that lists the number of error events for each distance between spect.dfree and spect.dfree+n-1. The vector represents the first n components of the distance spectrum.

Algorithms

The function uses a tree search algorithm implemented with a stack, as described in [2].

References

[1] Bocharova, I.E., and B.D. Kudryashov. “Rational Rate Punctured Convolutional Codes for Soft-Decision Viterbi Decoding.” IEEE Transactions on Information Theory 43, no. 4 (July 1997): 1305–13. https://doi.org/10.1109/18.605600.

[2] Cedervall, M.L., and R. Johannesson. “A Fast Algorithm for Computing Distance Spectrum of Convolutional Codes.” IEEE Transactions on Information Theory 35, no. 6 (November 1989): 1146–59. https://doi.org/10.1109/18.45271.

[3] Chang J., D. Hwang, and M. Lin. “Some Extended Results on the Search for Good Convolutional Codes.” IEEE Transactions on Information Theory 43, no. 5 (September 1997): 1682–97. https://doi.org/10.1109/18.623175.

[4] Frenger, P.K., P. Orten, and T. Ottosson. “Comments and Additions to Recent Papers on New Convolutional Codes.” IEEE Transactions on Information Theory 47, no. 3 (March 2001): 1199–1201. https://doi.org/10.1109/18.915683.

Version History

Introduced before R2006a

See Also

Functions