Main Content

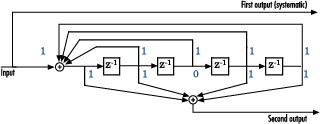
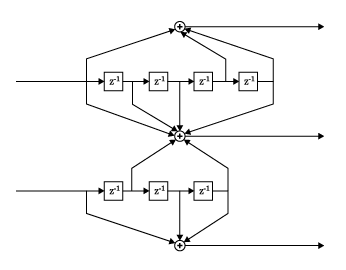
convenc

Convolutionally encode binary message

collapse all in page

Syntax

codedout = convenc(msg,trellis)
codedout = convenc(msg,trellis,puncpat)
codedout = convenc(___,istate)
[codedout,fstate] = convenc(___)

Description

codedout = convenc(msg,trellis) encodes the input binary message by using a convolutional encoder represented by a trellis structure. For details about trellis structures in MATLAB®, see Trellis Description of a Convolutional Code. The input message contains one or more symbols, each of which consists of log2(trellis.numInputSymbols) bits. The coded output, codedout, contains one or more symbols, each of which consists of log2(trellis.numOutputSymbols) bits.

example

codedout = convenc(msg,trellis,puncpat)specifies a puncture pattern, puncpat, to enable higher rate encoding than unpunctured coding.

For some commonly used puncture patterns for specific rates and polynomials, see the last three references.

example

codedout = convenc(___,istate) enables the encoder registers to start at a state specified by istate. Specify istate as the last input parameter preceded by any of the input argument combinations in the previous syntaxes.

example

[codedout,fstate] = convenc(___) also returns the final state of the encoder. When calling convenc iteratively, fstate is typically used to set istate for subsequent calls to the convenc function.

example

Examples

collapse all

Open Live Script

Create convolutional codes by using a trellis structure. You can define the trellis by using the poly2trellis function or by manually specifying the trellis structure. The example shows both methods.

Define trellis by using poly2trellis function

Define the trellis structure to be used to configure the encoder by using the poly2trellis function. 

trellis_a = poly2trellis([5 4],[23 35 0; 0 5 13])
trellis_a = struct with fields:
     numInputSymbols: 4
    numOutputSymbols: 8
           numStates: 128
          nextStates: [128x4 double]
             outputs: [128x4 double]

Use the trellis structure to configure the convenc function. Encode five two-bit symbols for a K/N rate 2/3 convolutional code by using the convenc function.

K = log2(trellis_a.numInputSymbols) % Number of input bit streams
K = 
2

N = log2(trellis_a.numOutputSymbols) % Number of output bit streams
N = 
3

numReg = log2(trellis_a.numStates) % Number of coder registers
numReg = 
7

numSymPerFrame = 5; % Number of symbols per frame
data = randi([0 1],K*numSymPerFrame,1);
[code_a,fstate_a] = convenc(data,trellis_a);

Verify that the encoded output is 15 bits, which is 3/2 (N/K) times the length of the input sequence, data.

code_a'
ans = 1×15

     1     1     1     0     0     1     1     1     1     1     0     1     0     1     0


length(data)
ans = 
10

length(code_a)
ans = 
15

Define trellis manually

Manually define a trellis structure for a K/N rate 1/2 convolutional code.

trellis_b = struct('numInputSymbols',2,'numOutputSymbols',4, ...
'numStates',4,'nextStates',[0 2;0 2;1 3;1 3], ...
'outputs',[0 3;1 2;3 0;2 1])
trellis_b = struct with fields:
     numInputSymbols: 2
    numOutputSymbols: 4
           numStates: 4
          nextStates: [4x2 double]
             outputs: [4x2 double]

Use the trellis structure to configure the convenc function when encoding 10 one-bit symbols.

K = log2(trellis_b.numInputSymbols) % Number of input bit streams
K = 
1

N = log2(trellis_b.numOutputSymbols) % Number of output bit streams
N = 
2

numReg = log2(trellis_b.numStates) % Number of coder registers
numReg = 
2

numSymPerFrame = 10; % Number of symbols per frame
data = randi([0 1],K*numSymPerFrame,1);
code_b = convenc(data,trellis_b);

Verify that the encoded output is 20 bits, which is 2/1 (N/K) times the length of the input sequence, data.

code_b'
ans = 1×20

     0     0     1     1     0     0     1     0     1     0     1     1     0     1     1     1     0     0     0     1


length(data)
ans = 
10

length(code_b)
ans = 
20
Open Live Script

Use puncturing to adjust the K/N code rate of the convolutional encoder from 1/2 to 3/4.

Initialize parameters for the encoding operation.

trellis = poly2trellis(7,[171 133])
trellis = struct with fields:
     numInputSymbols: 2
    numOutputSymbols: 4
           numStates: 64
          nextStates: [64x2 double]
             outputs: [64x2 double]


puncpat = [1;1;0];

Calculate the unpunctured and punctured code rates.

K = log2(trellis.numInputSymbols); % Number of input streams
N = log2(trellis.numOutputSymbols); % Number of output streams
unpunc_coderate = K/N; % Unpunctured code rate
punc_coderate = (K/N)*length(puncpat)/sum(puncpat); % Punctured code rate
fprintf(['K is %d and N is %d. ' ...
    'The unpunctured code rate is %3.2f ' ...
    'and the punctured code rate is %3.2f.\n'], ...
    K,N,unpunc_coderate,punc_coderate)
K is 1 and N is 2. The unpunctured code rate is 0.50 and the punctured code rate is 0.75.

Convolutionally encode an all 1s three-bit message without puncturing applied to the coded output. Then, convolutionally encode the same message with puncturing.

msg = ones(length(puncpat),1);
unpuncturedcode = convenc(msg,trellis);
puncturedcode = convenc(msg,trellis,puncpat);

Show the message, the unpunctured code, the punctured code, and the puncture pattern.

msg'
ans = 1×3

     1     1     1


unpuncturedcode'
ans = 1×6

     1     1     0     1     1     0


puncpat'
ans = 1×3

     1     1     0


puncturedcode'
ans = 1×4

     1     1     1     1

Without puncturing, the configured convolutional encoding inputs three message bits and outputs six coded bits. Confirm the resulting code rate matches the expected code rate of 1/2.

length(msg)/length(unpuncturedcode)
ans = 
0.5000

With puncturing, bits in positions 1 and 2 of the input message are transmitted, while the bit in position 3 is removed. For every three bits of input, the punctured code generates four bits of output. Confirm the resulting code rate matches the expected code rate of 3/4.

length(msg)/length(puncturedcode)
ans = 
0.7500
Open Live Script

Use a trellis structure to configure the rate 1/2 feedforward convolutional code in this diagram.

Diagram of a rate 1/2 feedforward convolutional encoder with codegenerators [6 7] and constraint length 3

Create a trellis structure, setting the constraint length to 3 and specifying the code generator as a vector of octal values. The diagram indicates the binary values and polynomial form, indicating the left-most bit is the most-significant-bit (MSB). The binary vector [1 1 0] represents octal 6 and corresponds to the upper row of binary digits in the diagram. The binary vector [1 1 1] represents octal 7 and corresponds to the lower row of binary digits in the diagram. These binary digits indicate connections from the outputs of the registers to the two adders in the diagram. 

trellis = poly2trellis(3,[6 7])
trellis = struct with fields:
     numInputSymbols: 2
    numOutputSymbols: 4
           numStates: 4
          nextStates: [4x2 double]
             outputs: [4x2 double]

Generate random binary data. Convolutionally encode the data, by using the specified trellis structure. Decode the coded data by using the Viterbi algorithm with the specified trellis structure, 34 for its traceback depth, truncated operation mode, and hard decisions.

data = randi([0 1],70,1);
codedData = convenc(data,trellis);
tbdepth = 34;
decodedData = vitdec(codedData,trellis,tbdepth,'trunc','hard');

Verify the decoded data has zero bit errors.

biterr(data,decodedData)
ans = 
0
Open Live Script

Create a trellis structure to represent the rate 1/2 systematic convolutional encoder with feedback shown in this diagram.

This encoder has 5 for its constraint length, [37 33] as its generator polynomial matrix, and 37 for its feedback connection polynomial.

The first generator polynomial is octal 37. The second generator polynomial is octal 33. The feedback polynomial is octal 37. The first generator polynomial matches the feedback connection polynomial because the first output corresponds to the systematic bits.

The binary vector [1 1 1 1 1] represents octal 37 and corresponds to the upper row of binary digits in the diagram. The binary vector [1 1 0 1 1] represents octal 33 and corresponds to the lower row of binary digits in the diagram. These binary digits indicate connections from the outputs of the registers to the two adders in the diagram. The initial 1 corresponds to the input bit.

Convert the polynomial to a trellis structure by using the poly2trellis function. When used with a feedback polynomial, poly2trellis makes a feedback connection to the input of the trellis.

trellis = poly2trellis(5,[37 33],37)
trellis = struct with fields:
     numInputSymbols: 2
    numOutputSymbols: 4
           numStates: 16
          nextStates: [16x2 double]
             outputs: [16x2 double]

Generate random binary data. Convolutionally encode the data by using the specified trellis structure. Decode the coded data by using the Viterbi algorithm with the specified trellis structure, 34 for its traceback depth, truncated operation mode, and hard decisions.

data = randi([0 1],70,1);
codedData = convenc(data,trellis);
tbdepth = 34; % Traceback depth for Viterbi decoder
decodedData = vitdec(codedData,trellis,tbdepth,'trunc','hard');

Verify the decoded data has zero bit errors.

biterr(data,decodedData)
ans = 
0
Open Live Script

Compare the convolutional encoding of a full message to the convolutional encoding of a message in two segments.

This diagram shows a rate 2/3 encoder with two input streams, three output streams, and seven shift registers.

Define the trellis structure in the diagram by using the poly2trellis function. Set the constraint length of the upper path to 5 and the constraint length of the lower path to 4. The octal representation of the code generator matrix corresponds to the taps from the upper and lower shift registers.

trellis = poly2trellis([5 4],[23 35 0; 0 5 13]);

Inspect the coder configuration.

K = log2(trellis.numInputSymbols) % Number of input bit streams
K = 
2

N = log2(trellis.numOutputSymbols) % Number of output bit streams
N = 
3

coderate = K/N
coderate = 
0.6667

numReg = log2(trellis.numStates) % Number of coder registers
numReg = 
7

Define a message with five two-bit input symbols.

numSymPerFrame = 5; % Number of symbols per frame
msg = randi([0 1],K*numSymPerFrame,1);

Encode the full message by using the trellis to configure the convenc function.

[code_a,fstate_a] = convenc(msg,trellis);

Apply piecewise message encoding by using the same trellis structure. Use the final and initial state arguments when using the convenc function. For piecewise message encoding, message segments must be a multiple of the number of bits in an input symbol.

Encode part of the message, recording the final state for later use. 

[code_a1,fstate_a1] = convenc(msg(1:6),trellis);

Encode the rest of the message, using the final state, fstate_a1, as the initial state input argument.

[code_a2,fstate_a2] = convenc(msg(7:end),trellis,fstate_a1);

Verify that the full coded message, code_a, matches the concatenated piecewise coded message, [code_a1; code_a2].

isequal(code_a,[code_a1; code_a2])
ans = logical
   1

Verify that the final state, fstate_a, of the encoder after the full message encoding matches the final state, fstate_a2, of the encoder after piecewise message encoding.

isequal(fstate_a,fstate_a2)
ans = logical
   1

Input Arguments

collapse all

Binary message, specified as a vector of binary values. msg must contain one or more symbols. Each symbol must consist of log2(trellis.numInputSymbols) bits.

Example: [1 1 0 1 0 0 1 1] specifies the message as a binary row vector with eight elements.

Data Types: double | logical

Trellis description, specified as a MATLAB structure that contains the trellis description for a rate K/N code. K represents the number of input bit streams, and N represents the number of output bit streams.

The trellis structure contains these fields. You can either use the poly2trellis function to create the trellis structure or create it manually. For more about this structure, see Trellis Description of a Convolutional Code and the istrellis function.

Number of symbols input to the encoder, specified as an integer equal to 2K, where K is the number of input bit streams.

Number of symbols output from the encoder, specified as an integer equal to 2N, where N is the number of output bit streams.

Number of states in the encoder, specified as a power of 2.

Next states for all combinations of current states and current inputs, specified as a matrix of integers. The matrix size must be numStates by 2K.

Outputs for all combinations of current states and current inputs, specified as a matrix of octal numbers. The matrix size must be numStates by 2K.

Data Types: struct

Puncture pattern, specified as a vector of binary values. Indicate punctured bits with 0s and unpunctured bits with 1s. The length of the puncpat vector must be an integer divisor of the input message vector length, length(msg).

Data Types: double

Initial state used for the encoder registers, specified as an integer scalar in the range [0, (trellis.numStates – 1)].

Data Types: double

Output Arguments

collapse all

Convolutionally encoded message, returned as a vector of binary values. This output vector has the same data type and orientation as input msg. Each symbol in codedout consists of log2(trellis.numOutputSymbols) bits.

Data Types: double | logical

Final state of the encoder registers, returned as an integer scalar. When calling convenc iteratively, such as in a loop, fstate is typically used to set istate for subsequent calls to the convenc function.

Data Types: double

More About

collapse all

Convolutional Coding

Convolutional coding is an error-control coding that has memory. Specifically, the computations and coded output depend on the current set of input symbols and on a number of previous input symbols that varies depending on the trellis configuration. A convolutional encoder outputs N bits for every K input bits. The input can have varying multiples of K bits over a simulation.

Using a MATLAB trellis structure that defines a set of generator polynomials, you can model nonsystematic, systematic feedforward, or systematic feedback convolutional codes. For more information and examples that demonstrate various convolutional code architectures, see the Convolutional Codes topic.

To decode the convolutionally coded output, you can use:

  • The vitdec function or comm.ViterbiDecoder System object™ — Uses the Viterbi algorithm with hard-decision and soft-decision decoding

  • The comm.APPDecoder System object — Uses an a posteriori probability decoder for the soft output decoding of convolutional codes

References

[1] Clark, George C., and J. Bibb Cain. Error-Correction Coding for Digital Communications. Applications of Communications Theory. New York: Plenum Press, 1981.

[2] Gitlin, Richard D., Jeremiah F. Hayes, and Stephen B. Weinstein. Data Communications Principles. Applications of Communications Theory. New York: Plenum Press, 1992.

[3] Yasuda, Y., K. Kashiki, and Y. Hirata. “High-Rate Punctured Convolutional Codes for Soft Decision Viterbi Decoding.” IEEE® Transactions on Communications 32, no. 3 (March 1984): 315–19. https://doi.org/10.1109/TCOM.1984.1096047.

[4] Haccoun, D., and G. Begin. “High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding.” IEEE Transactions on Communications 37, no. 11 (November 1989): 1113–25. https://doi.org/10.1109/26.46505.

[5] Begin, G., D. Haccoun, and C. Paquin. “Further Results on High-Rate Punctured Convolutional Codes for Viterbi and Sequential Decoding.” IEEE Transactions on Communications 38, no. 11 (November 1990): 1922–28. https://doi.org/10.1109/26.61470.

Extended Capabilities

Version History

Introduced before R2006a

See Also

Functions

Objects

Topics