DPD Coefficient Estimator
Estimate memory-polynomial coefficients for digital predistortion
Libraries:
Communications Toolbox /
RF Impairments Correction
Description
Estimate the coefficients of a memory polynomial for digital pre-distortion (DPD) of a nonlinear power amplifier, given the baseband equivalent input and baseband equivalent output of the power amplifier. For more information, see Digital Predistortion and Optimizing Estimator Polynomial Degree and Memory Depth.
This icon shows the block with all ports enabled.
![]()
Examples
Apply digital predistortion (DPD) to a 16-QAM signal of random symbols. The DPD Coefficient Estimator block uses a captured signal containing from input and output signals from a power amplifier (PA) to determine the predistortion coefficient matrix. Digital predistortion of the signal preconditions is to correct impairments that the PA introduces. This model does not include a block representing the PA.
The PreLoadFcn callback initializes model parameters, and also loads workspace variables PA_Input and PA_Output from the file commpowamp_dpd_data.mat. For more information, see Model Callbacks (Simulink).
The PA_Input and PA_Output variables are baseband-equivalent signals captured at the input and output of a PA. PA_Input and PA_Output are used by the DPD Coefficient Estimator block to estimate the memory-polynomial coefficients. The memory-polynomial coefficients are input to the DPD block to predistort the PA input signal.
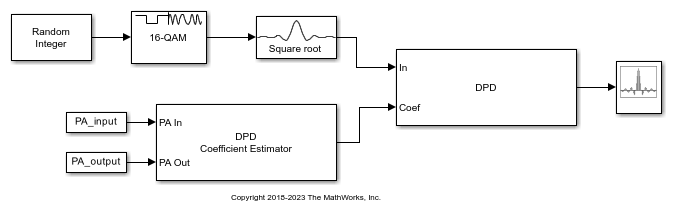
The input signal path of the model generates a random symbol stream, applies 16-QAM modulation, and then applies raised-cosine transmit filtering to the modulated signal.
The input signal is digitally predistorted in the DPD block using the memory-polynomial coefficients generated in the DPD Coefficient Estimator block. The DPD block returns the predistorted input signal for the PA that produced the distorted PA output signal.
Ports
Input
Power amplifier baseband-equivalent input, specified as a column vector.
Data Types: double
Complex Number Support: Yes
Power amplifier baseband-equivalent output, specified as a column vector of the same length as PA In.
Data Types: double
Complex Number Support: Yes
Forgetting factor used by the recursive least squares algorithm, specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the convergence time but causes the output estimates to be less stable.
Dependencies
To enable this port, set Algorithm to Recursive least squares and
set Forgetting factor
source to Input port.
Data Types: double
Output
Memory-polynomial coefficients, returned as a matrix. For more information, see Digital Predistortion.
This port is unnamed on the block.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Desired amplitude gain in dB, specified as a scalar. This parameter value expresses the desired signal gain at the compensated amplifier output.
In addition to linearization, the DPD should make the combined gain between the DPD input and the power amplifier output as close as possible to the expected gain. Therefore, set this parameter based on the expected gain of the power amplifier that you obtain during PA characterization.
Tunable: Yes
Polynomial type used for predistortion, specified as one of these values:
Memory polynomial— Computes predistortion coefficients by using a memory polynomial without cross termsCross-term memory polynomial— Computes predistortion coefficients by using a memory polynomial with cross terms
For more information, see Digital Predistortion.
Memory-polynomial degree, specified as a positive integer.
Memory-polynomial depth in samples, specified as a positive integer.
Adaptive algorithm used for equalization, specified as one of these values:
Least squares— Estimate the memory-polynomial coefficients by using a least squares algorithmRecursive least squares— Estimate the memory-polynomial coefficients by using a recursive least squares algorithm
For algorithm reference material, see the works listed in [1] and [2].
Source of the forgetting factor, specified as one of these values:
Property— Specify this value to use the Forgetting factor parameter to specify the forgetting factor.Input port— Specify this value to use the Forgetting factor input port to specify the forgetting factor.
Dependencies
To enable this parameter, set Algorithm
to Recursive least squares.
Forgetting factor used by the recursive least squares algorithm, specified as a scalar in the range (0, 1]. Decreasing the forgetting factor reduces the convergence time but causes the output estimates to be less stable.
Dependencies
To enable this parameter, set Algorithm
to Recursive least squares and set Forgetting factor
source to Property.
Initial coefficient estimate for the recursive least squares algorithm, specified as a matrix of real or complex values.
If you specify this value as an empty matrix, the initial coefficient estimate for the recursive least squares algorithm is chosen automatically to correspond to a memory polynomial that is an identity function, so that the output is equal to input.
If you specify this value as a nonempty matrix, the number of rows must be equal to the Memory depth parameter value.
If the Polynomial type parameter is set to
Memory polynomial, the number of columns is the degree of the memory polynomial.If the Polynomial type parameter is set to
Cross-term memory polynomial, the number of columns must equal m(n-1)+1. m is the memory depth of the polynomial, and n is the degree of the memory polynomial.
For more information, see Digital Predistortion.
Dependencies
To enable this parameter, set Algorithm
to Recursive least squares.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
Wireless communication transmissions commonly require wide bandwidth signal transmission over a wide signal dynamic range. To transmit signals over a wide dynamic range and achieve high efficiency, RF power amplifiers (PAs) commonly operate in their nonlinear region. As this constellation diagram shows, the nonlinear behavior of a PA causes signal constellation distortions that pinch the amplitude (AM-AM distortion) and twist phase (AM-PM distortion) of constellation points proportional to the amplitude of the constellation point.

The goal of digital predistortion is to find a nonlinear function that linearizes the net effect of the PA nonlinear behavior at the PA output across the PA operating range. When the PA input is x(n), and the predistortion function is f(u(n)), where u(n) is the true signal to be amplified, the PA output is approximately equal to G×u(n), where G is the desired amplitude gain of the PA.

The digital predistorter can be configured to use a memory polynomial with or without cross terms.
The memory polynomial with cross terms predistorts the input signal as
The memory polynomial with cross terms has (M+M×M×(K-1)) coefficients for cm and amjk.
The memory polynomial without cross terms predistorts the input signal as
The polynomial without cross terms has M×K coefficients for amk.
Estimating Predistortion Function and Coefficients
The DPD coefficient estimation uses an indirect learning architecture to find function f(u(n)) to predistort input signal u(n) which precedes the PA input.
The DPD coefficient estimation algorithm models nonlinear PA memory effects based on the work in reference papers by Morgan, et al [1], and by Schetzen [2], using the theoretical foundation developed for Volterra systems.
Specifically, the inverse mapping from the PA output normalized by the PA gain, {y(n)/G}, to the PA input, {x(n)}, provides a good approximation to the function f(u(n)), needed to predistort {u(n)} to produce {x(n)}.
Referring to the memory polynomial equations above, estimates are computed for the memory-polynomial coefficients:
cm and amjk for a memory polynomial with cross terms
amk for a memory polynomial without cross terms
The memory-polynomial coefficients are estimated by using a least squares fit algorithm or a recursive least squares algorithm. The least squares fit algorithm or a recursive least squares algorithms use the memory polynomial equations above for a memory polynomial with or without cross terms, by replacing {u(n)} with {y(n)/G}. The function order and dimension of the coefficient matrix are defined by the degree and depth of the memory polynomial.
For an example that details the process of accurately estimating memory-polynomial coefficients and predistorting a PA input signal, see Digital Predistortion to Compensate for Power Amplifier Nonlinearities.
For background reference material, see the works listed in [1] and [2].
The DPD coefficient estimator based on [1] offers one specific indirect learning architecture, and may not be an optimal estimator. Other estimators, such as those using a direct learning architecture, may achieve better DPD results.
With the indirect learning architecture coefficient estimator, choosing the optimal degree and memory depth for the DPD coefficient estimator is a manual and iterative process. Consider starting by using a DPD coefficient estimator that has the same degree and the memory depth as that of the PA model, and check the DPD results. Assuming the results look promising, try reducing the degree and the memory depth for the DPD coefficient estimator. If DPD results are roughly the same or better, consider using the smaller degree and a smaller memory depth for the DPD coefficient estimator because it will be less computationally intensive. You should also experiment with degrees and memory depths above the degree and the memory depth of the PA model. If DPD performance improves using a higher degree or a larger memory depth for the DPD coefficient estimator may be desirable.
Regardless of the polynomial degree used for the estimator, you must control the bandwidth of the DPD input signal to avoid aliasing due to nonlinearities. As a rule of thumb, set the oversampling ratio of the DPD input signal equal to or greater than the degree of the DPD memory polynomial.
References
[1] Morgan, Dennis R., Zhengxiang Ma, Jaehyeong Kim, Michael G. Zierdt, and John Pastalan. "A Generalized Memory Polynomial Model for Digital Predistortion of Power Amplifiers." IEEE® Transactions on Signal Processing. Vol. 54, Number 10, October 2006, pp. 3852–3860.
[2] M. Schetzen. The Volterra and Wiener Theories of Nonlinear Systems. New York: Wiley, 1980.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2019a
See Also
Blocks
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)