Gold Sequence Generator

Generate Gold sequence from set of sequences

Libraries:
Communications Toolbox / Comm Sources / Sequence Generators

Description

The Gold Sequence Generator block generates a binary sequence with small periodic cross-correlation properties from a bounded set of sequences. For more information, see Gold Sequences.

This block can output sequences that vary in length during simulation. For more information about variable-size signals, see Variable-Size Signal Basics (Simulink).

These icons shows the block with all ports enabled.

Gold Sequence Generator block showing optional input ports for output size and reset

Examples

expand all

Generate Gold Code Sequence

This example uses:

Open Model

Generate the same Gold code sequences using two PN Sequence Generator blocks or one Gold Sequence Generator block.

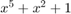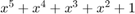Two PN Sequence Generator blocks and one Gold code sequence block are configured to output the gold sequence resulting from preferred polynomials $x^5+x^2+1$ and $x^5+x^4+x^3+x^2+1$ . For the PN Sequence Generator blocks, an XOR block combines the output and saves the resulting sequence to the workspace variable out.pn_seq_xor. The Gold Sequence Generator block saves its output sequence to the workspace variable out.gold_seq.

Run the model and compare the outputs.

The XORd PN sequence output is:

pn_seq_xor =

     0     0     0     0     0     0     1     0     1     1     1

The Gold sequence output is:

gold_seq =

     0     0     0     0     0     0     1     0     1     1     1

To explore further, change the Sequence index parameter in the Gold Sequence Generator block and add a delay for the second PN Sequence Generator block.

Gold Sequence Generator Reset Behavior

This example uses:

Open Model

This example shows the Gold Sequence Generator output behavior for reset related parameter settings.

Three Gold code sequence blocks are configured to output the gold sequence resulting from various reset conditions.

For no reset, the Samples per frame parameter is set to 1 and the output is saved to out.y1.

For reset by using a scalar input Rst signal, the Samples per frame parameter is set to 1 for the Signal From Workspace and Gold Sequence Generator blocks. The output is saved to out.y2.

For reset by using a vector input Rst signal, the Samples per frame parameter is set to 8 for the Signal From Workspace and Gold Sequence Generator blocks. The output is saved to out.y3.

The scalar and vector reset signal value is [0 0 0 1 0 0 0 0]. When the Rst input port in enabled, the Gold Sequence Generator block resets the output sequence at the fourth sample. Run the model and compare the outputs.

The sequence output when no reset occurs is:
0  0  1  1  1  0  1  0
The sequence output when using a scalar reset signal is:
0  0  1  0  0  1  1  1
The sequence output when using a vector reset signal is:
0  0  1  0  0  1  1  1

The values output to out.y2 and out.y3 are equal because they are reset on the same sample and the length of the output is also equal because of the simulation stop time setting.

isequal(out.y2,out.y3) returns: 1

The Gold Sequence generator block always rounds up to output a multiple of the Samples per frame setting. Change the simulation stop time to 10 and the output sequence lengths are no longer equal.

The sequence output when no reset occurs is:
0  0  1  1  1  0  1  0  0  0  1
The sequence output when using a scalar reset signal is:
0  0  1  0  0  1  1  1  0  1  0
The sequence output when using a vector reset signal is:
0  0  1  0  0  1  1  1  0  1  0  0  0  1  1  1

Generate GPS Coarse Acquisition Codes

This example uses:

Open Model

This model shows how to configure the Gold Sequence Generator block to generate coarse acquisition (C/A) codes as presented in [ 1 ] and uses a discrete block model representation of the same configuration for validating the code generated. GPS uses C/A codes to facilitate acquisition and tracking of transmission signals.

Explore Model

The model contains a discrete block model C/A codes as presented in [ 1 ] and configures the Gold Sequence Generator block to generate the same codes.

To produce the GPS C/A codes, the configuration of the Gold Sequence Generator block requires consideration of these setup details.

Primitive polynomials (g1 and g2) and code phases (m2), specified in the PreLoadFcn callback of the model matching the discrete block model and the descending ordered polynomials in [ 1 ].
g1, g2, and m2 are used to configure the Preferred polynomial (1), Preferred polynomial (2), and Sequence index parameters of the Gold Sequence Generator block.
In [ 1 ], the polynomials are interpreted as descending ordered, so the Gold Sequence Generator block uses the fliplr function to flip the g1, g2, and m2 binary vectors to match the discrete block model configuration.
The Sequence index parameter corresponds to the delayed second code of the discrete block model. In the discrete block implementation, the shift registers are XOR'd to achieve this mask shift. During initialization, the mask2shift function converts the specified mask to the scalar delay used by the Gold Sequence generator block.
The feedback register configuration must remain static for the duration of the simulation.

Comparing Results

After running the model, the isequal is used to compare the GPS C/A codes produced by using the discrete block model and the Gold Sequence Generator block.

isequal(G1_Output,code1) = 1
isequal(G2_Output,code2) = 1
isequal(gps_ca,goldseq) = 1

References

Tsui, James Bao-Yen. Fundamentals of Global Positioning System Receivers: A Software Approach. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2004. https://doi.org/10.1002/0471712582.

Extended Examples

WCDMA End-to-End Physical Layer

Part of the frequency division duplex (FDD) downlink physical layer of the third generation wireless communication system known as wideband code division multiple access (WCDMA).

Open Script

Ports

Input

expand all

oSiz — Current output size
scalar | two-element row vector

Current output size, specified as a scalar or a two-element row vector. The second element of the vector must be 1.

Example: [10 1] indicates the current output column vector will be of size 10-by-1.

Dependencies

To enable this port select the Output variable-size signals parameter and set Maximum output size source to Dialog parameter.

Data Types: double

Ref — Reference input signal
scalar | column vector

Reference input signal, specified as a scalar, column vector.

Dependencies

To enable this port select the Output variable-size signals parameter and set Maximum output size source to Inherit from reference input.

Data Types: double

Rst — Reset signal
scalar | column vector

Reset signal, specified in one of these forms.

When the output size is variable specify as a scalar.
Otherwise, specify as a scalar or a 2-D column vector with a length equal to Samples per frame.

The output signal resets for nonzero Rst input values. For more information, see Reset Behavior

Dependencies

To enable this port, select the Reset on nonzero input parameter.

Data Types: double

Output

expand all

Out — Output signal
binary column vector

Output signal, returned as a binary column vector. At least one element of the Initial states (1) or Initial states (2) vector must be nonzero in order for the block to generate a nonzero sequence.

Data Types: double

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Preferred polynomial (1) — First sequence polynomial
`'z^6 + z + 1'` (default) | polynomial character vector | binary row vector | integer row vector

First sequence polynomial, specified in one of these forms.

Character vector or string scalar of a polynomial whose constant term is 1. For more information, see Representation of Polynomials in Communications Toolbox.
Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be 1, indicating the leading term with degree N and a constant term of 1.
Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be 0, indicating a constant term of 1.

This property determines the feedback connections for the shift register of the first preferred PN sequence generator. The degree of the first generator polynomial must equal the degree of the second generator polynomial specified by the Preferred polynomial (2) parameter. For more information, see Preferred Pairs of Sequences.

Example: 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0 1], and [8 2 0] represent the same polynomial, p(z) = z⁸ + z² + 1.

Initial states (1) — Initial states for first sequence polynomial
`[0 0 0 0 0 1]` (default) | binary vector

Initial states of the shift register for first sequence polynomial of the preferred pair, specified as a binary vector with length equal to the degree of Preferred polynomial (1).

Note

For the block to generate a nonzero sequence, at least one element of the initial conditions for the first or second preferred PN sequence generator must be nonzero. Specifically, the initial state of at least one of the shift registers must be nonzero.

Preferred polynomial (2) — Second sequence polynomial
`'z^6 + z^5 + z^2 + z + 1'` (default) | polynomial character vector | binary row vector | integer row vector

Second sequence polynomial, specified in one of these forms.

Character vector or string scalar of a polynomial whose constant term is 1. For more information, see Representation of Polynomials in Communications Toolbox.
Binary-valued row vector that represents the coefficients of the polynomial in order of descending powers. The length of this vector must be N + 1, where N is the degree of the polynomial. The first and last entries must be 1, indicating the leading term with degree N and a constant term of 1.
Integer-valued row vector of elements that represent the exponents for the nonzero terms of the polynomial in order of descending powers. The last entry must be 0, indicating a constant term of 1.

This property determines the feedback connections for the shift register of the first preferred PN sequence generator. The degree of the second generator polynomial must equal the degree of the first generator polynomial specified by the Preferred polynomial (1) parameter. For more information, see Preferred Pairs of Sequences.

Example: 'z^8 + z^2 + 1', [1 0 0 0 0 0 1 0 1], and [8 2 0] represent the same polynomial, p(z) = z⁸ + z² + 1.

Initial states (2) — Initial states for second sequence polynomial
`[0 0 0 0 0 1]` (default) | binary vector

Initial states of the shift register for second sequence polynomial of the preferred pair, specified as a binary vector with length equal to the degree of Preferred polynomial (2).

Note

Sequence index — Sequence index
`0` (default) | integer scalar in the range [–2, 2ⁿ–2]

Sequence index of the output sequence from the set of sequences, specified as an integer scalar in the range [–2, 2ⁿ–2]. n is the degree of the preferred polynomials. For more information, see Gold Sequences.

Shift — Offset of Gold sequence
`0` (default) | integer scalar

Offset of Gold sequence from the initial time, specified as an integer scalar.

Output variable-size signals — Option to output variable-length signals
`off` (default) | `on`

Select this parameter to enable variable-length output sequences during simulation. When you clear this parameter, the block outputs fixed-length sequences. When you select this parameter, the block can output variable-length sequences. For information about variable-size signals, see Variable-Size Signal Basics (Simulink).

Maximum output size source — Maximum output size source
`Dialog parameter` (default) | `Inherit from reference port`

Select how to specify the maximum sequence output size.

Dialog parameter — Select this value to configure the block to use the Maximum output size parameter setting as the maximum permitted output sequence length. The oSiz input port specifies the current size of the output signal, and the block output inherits the sample time from the input signal. The input value of oSiz must be less than or equal to the Maximum output size parameter.
Inherit from reference port — Select this value to enable the Ref input port and configure the block to inherit the sample time, maximum size, and current output size from the variable-sized signal at the Ref input port. These set the maximum permitted output sequence length.

Dependencies

To enable this parameter, select Output variable-size signals.

Maximum output size — Maximum output size
`[10 1]` (default) | vector of the form [n 1]

Specify the maximum output size for the block. n is a positive scalar.

Example: [10 1] specifies a 10-by-1 maximum size for the output signal.

Dependencies

To enable this parameter, select Output variable-size signals and set Maximum output size source to Dialog parameter.

Sample time — Output sample time
`1` (default)

Positive scalars specify the time in seconds between each sample of the output signal. If you set the sample time to -1, the output signal inherits the sample time from downstream. For information on the relationship between the Sample time and Samples per frame parameters, see Sample Timing.

Dependencies

To enable this parameter do not select Output variable-size signals.

Samples per frame — Samples per frame
`1` (default) | positive integer

Samples per frame, specified as a positive integer indicating the number of samples per frame in one channel of the output data. For information on the relationship between Sample time and Samples per frame, see Sample Timing.

Dependencies

To enable this parameter do not select Output variable-size signals.

Reset on nonzero input — Reset output signal
`off` (default) | `on`

Select this parameter to enable the Rst port. When a nonzero value is input at the Rst port, the internal shift registers are reset to the original values of the Initial states (1) and Initial states (2) parameters.

Output data type — Output data type
`double` (default) | `boolean` | `Smallest unsigned integer`

Output data type, specified as boolean, double, or Smallest unsigned integer.

When set to Smallest unsigned integer, the output data type is selected based on the settings used in the Hardware Implementation Pane (Simulink) of the Configuration Parameters dialog box of the model. If ASIC/FPGA is selected in the Hardware Implementation pane, the output data type is the ideal minimum one-bit size (ufix(1)). For all other selections, it is an unsigned integer with the smallest available word length large enough to fit one bit, usually corresponding to the size of a char (uint8).

Block Characteristics

Data Types	`Boolean` \| `double` \| `fixed point`
Multidimensional Signals	`no`
Variable-Size Signals	`yes`

More About

expand all

Sample Timing

The time between output updates is equal to the product of the Samples per frame and Sample time parameter values. For example, if Sample time and Samples per frame each equal 1, the block outputs one sample every second. If you increase Samples per frame to 10, then the block outputs a 10-by-1 vector every 10 seconds. This timing ensures that the equivalent output rate is not dependent on the Samples per frame parameter.

Gold Sequences

The characteristic cross-correlation properties of Gold sequences make them useful when multiple devices are broadcasting in the same frequency range. The Gold sequences are defined using a specified pair of sequences u and v, called a preferred pair, as defined in Preferred Pairs of Sequences. The u and v pair of sequences has a period N = 2ⁿ – 1, where n is the degree of the generator polynomials specified by the parameter. The set G(u, v) of Gold sequences is defined by

$G (u, v) = {u, v, u \oplus v, u \oplus T v, u \oplus T^{2} v, ..., u \oplus T^{N - 1} v}$

T represents the operator that shifts vectors cyclically to the left by one place, and $\oplus$ represents addition modulo 2. G(u,v) contains N + 2 sequences of period N.

Gold sequences have the property that the cross-correlation between any two, or between shifted versions of them, takes on one of three values: –t(n), –1, or t(n) – 2, where

$t (n) = {\begin{array}{l} 1 + 2^{(n + 1) / 2} & n even \\ 1 + 2^{(n + 2) / 2} & n odd \end{array}$

The block uses two PN sequence generators to generate the preferred pair of sequences. The block then XORs these sequences to produce the output Gold sequence, as shown in this figure.

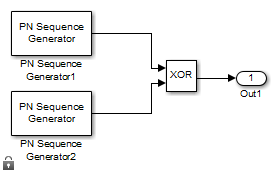
The Preferred polynomial (1) and Preferred polynomial (2) parameters determine the preferred pair of sequences and the feedback connections for the shift registers used by the PN sequence generators to generate their output. For more details on PN sequence generation, see the Simple Shift Register Generator section on the PN Sequence Generator block reference page.

This table provides examples of preferred pairs.

Degree of Generator Polynomials (n)	Pair of Sequences Period (N)	Preferred Polynomial (1) parameter value	Preferred Polynomial (2) parameter value
5	31	`[5 2 0]`	`[5 4 3 2 0]`
6	63	`[6 1 0]`	`[6 5 2 1 0]`
7	127	`[7 3 0]`	`[7 3 2 1 0]`
9	511	`[9 4 0]`	`[9 6 4 3 0]`
10	1023	`[10 3 0]`	`[10 8 3 2 0]`
11	2047	`[11 2 0]`	`[11 8 5 2 0]`

The Initial states (1) and Initial states (2) parameters are vectors specifying the initial values of the registers corresponding to Preferred polynomial (1) and Preferred polynomial (2), respectively.

Note

At least one element of the initial states vectors ( Initial states (1) or Initial states (2)) must be nonzero in order for the block to generate a nonzero sequence. Specifically, the initial state of at least one of the registers must be nonzero.

You can shift the starting point of the Gold sequence with the Shift parameter, which is an integer representing the length of the shift.

You can use an external signal to reset the values of the internal shift register to the initial state by selecting Reset on nonzero input. This creates an input port for the external signal in the block. The way the block resets the internal shift register depends on whether its output signal and the reset signal are scalar or vector. For more information, see Reset Behavior.

Preferred Pairs of Sequences

Preferred pairs of sequences, u and v, comprise the set of Gold sequences G(u, v).

For a pair of sequences, u and v, of period N = 2ⁿ–1 to be a preferred pair, they must satisfy these requirements:

n is the degree of the generator polynomials specified by the Preferred polynomial (1) and Preferred polynomial (2) parameters.
n is not divisible by 4.
v = u[q], where
- q is odd.
- q = 2^k+1 or q = 2^2k–2^k+1.
- v is obtained by sampling every qth symbol of u.
$\gcd (n, k) = {\begin{matrix} 1 & n \equiv 1 \mod 2 \\ 2 & n \equiv 2 \mod 4 \end{matrix}$

Sequence Index

The Sequence index parameter specifies which Gold sequence in the set G(u, v) is output. The range of Sequence index is [–2, –1, 0, 1, 2, ..., 2ⁿ–2], where n is the degree of the generator polynomials specified by the Preferred polynomial (1) and Preferred polynomial (2) parameters. This table shows the correspondence between Sequence index and the output sequence.

The sequence index specified by the Sequence index parameter specifies which Gold sequence in the set G(u, v) is output.

The set of available Gold sequences is

$G (u, v) = {u, v, u \oplus v, u \oplus T v, u \oplus T^{2} v, ..., u \oplus T^{N - 1} v}$

u and v are the two preferred PN sequences, T is the operator that shifts vectors cyclically to the left by one place, and $\oplus$ represents addition modulo 2. G(u,v) contains N+2 Gold sequences of period N = 2ⁿ–1.

The range of Sequence index is [–2, 2ⁿ–2], where n is the degree of the generator polynomials specified by the Preferred polynomial (1) and Preferred polynomial (2) parameters. The index values -2 and -1 correspond to the first and second preferred PN sequences as generated by Preferred polynomial (1) and Preferred polynomial (2), respectively. This table shows the correspondence between the sequence index and the output sequence.

Sequence Index	Output Sequence
–2	u
–1	v
0	$u \oplus v$
1	$u \oplus T v$
2	$u \oplus T^{2} v$
...	...
2 ⁿ –2	$u \oplus T^{2^{n} - 2} v$

Reset Behavior

Before you can reset the generator sequence, you must select the Reset on nonzero input parameter to enable the Rst input port. Suppose that the Gold Sequence Generator block outputs [1 0 0 1 1 0 1 1] when no reset exists. This table shows the effect on the Gold Sequence Generator block output for the parameter values indicated.

Reset Signal	Reset Signal Settings	Gold Sequence Generator block
No reset	Sample time is `1` Samples per frame is `1` Rst is `[0 0 0 0 0 0 0 0]`	Sample time is `1` Samples per frame is `1` Out is `[1 0 0 1 1 0 1 1]`
Scalar reset signal	Sample time is `1` Samples per frame is `1` Rst is `[0 0 0 1 0 0 0 0]`	Sample time = `1` Samples per frame is `1`
Vector reset signal	Sample time is `1` Samples per frame is `8` Rst is `[0 0 0 1 0 0 0 0]`	Sample time is `1` Samples per frame is `8`

For the no-reset case, the block outputs the sequence without resetting it. For the scalar and vector reset signal cases, the block inputs the reset signal [0 0 0 1 0 0 0 0] to the Rst port. Because the fourth bit of the reset signal is a 1 and Sample time is 1, the block resets the sequence output at the fourth bit.

For variable-sized outputs, the block supports only scalar reset signal inputs.

The Gold Sequence Generator Reset Behavior example demonstrates the reset behavior in a Simulink model.

References

[1] Proakis, John G. Digital Communications. 5th ed. New York: McGraw Hill, 2007.

[2] Gold, R. “Maximal Recursive Sequences with 3-Valued Recursive Cross-Correlation Functions (Corresp.).” IEEE^® Transactions on Information Theory 14, no. 1 (January 1968): 154–56. https://doi.org/10.1109/TIT.1968.1054106.

[3] Gold, R. “Optimal Binary Sequences for Spread Spectrum Multiplexing (Corresp.).” IEEE Transactions on Information Theory 13, no. 4 (October 1967): 619–21. https://doi.org/10.1109/TIT.1967.1054048.

[4] Sarwate, D.V., and M.B. Pursley. “Crosscorrelation Properties of Pseudorandom and Related Sequences.” Proceedings of the IEEE 68, no. 5 (1980): 593–619. https://doi.org/10.1109/PROC.1980.11697.

[5] Dixon, Robert C. Spread Spectrum Systems: With Commercial Applications. 3rd ed. New York: Wiley, 1994.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a

expand all

R2020a: Existing models automatically update this block to current version

Starting in R2020a, Simulink no longer allows you to use the Gold Sequence Generator block version available before R2015b.

Existing models automatically update to load the current Gold Sequence Generator block version. For more information on block forwarding, see Maintain Compatibility of Library Blocks Using Forwarding Tables (Simulink).

Gold Sequence Generator

Description

Examples

Generate Gold Code Sequence

Gold Sequence Generator Reset Behavior

Generate GPS Coarse Acquisition Codes

Extended Examples

WCDMA End-to-End Physical Layer

Ports

Input

oSiz — Current output size scalar | two-element row vector

Dependencies

Ref — Reference input signal scalar | column vector

Dependencies

Rst — Reset signal scalar | column vector

Dependencies

Output

Out — Output signal binary column vector

Parameters

Preferred polynomial (1) — First sequence polynomial 'z^6 + z + 1' (default) | polynomial character vector | binary row vector | integer row vector

Initial states (1) — Initial states for first sequence polynomial [0 0 0 0 0 1] (default) | binary vector

Preferred polynomial (2) — Second sequence polynomial 'z^6 + z^5 + z^2 + z + 1' (default) | polynomial character vector | binary row vector | integer row vector

Initial states (2) — Initial states for second sequence polynomial [0 0 0 0 0 1] (default) | binary vector

Sequence index — Sequence index 0 (default) | integer scalar in the range [–2, 2n–2]

Shift — Offset of Gold sequence 0 (default) | integer scalar

Output variable-size signals — Option to output variable-length signals off (default) | on

Maximum output size source — Maximum output size source Dialog parameter (default) | Inherit from reference port

Dependencies

Maximum output size — Maximum output size [10 1] (default) | vector of the form [n 1]

Dependencies

Sample time — Output sample time 1 (default)

Dependencies

Samples per frame — Samples per frame 1 (default) | positive integer

Dependencies

Reset on nonzero input — Reset output signal off (default) | on

Output data type — Output data type double (default) | boolean | Smallest unsigned integer

Block Characteristics

More About

Sample Timing

Gold Sequences

Preferred Pairs of Sequences

Sequence Index

Reset Behavior

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2020a: Existing models automatically update this block to current version

See Also

Blocks

Objects

oSiz — Current output size
scalar | two-element row vector

Ref — Reference input signal
scalar | column vector

Rst — Reset signal
scalar | column vector

Out — Output signal
binary column vector

Preferred polynomial (1) — First sequence polynomial
`'z^6 + z + 1'` (default) | polynomial character vector | binary row vector | integer row vector

Initial states (1) — Initial states for first sequence polynomial
`[0 0 0 0 0 1]` (default) | binary vector

Preferred polynomial (2) — Second sequence polynomial
`'z^6 + z^5 + z^2 + z + 1'` (default) | polynomial character vector | binary row vector | integer row vector

Initial states (2) — Initial states for second sequence polynomial
`[0 0 0 0 0 1]` (default) | binary vector

Sequence index — Sequence index
`0` (default) | integer scalar in the range [–2, 2ⁿ–2]

Shift — Offset of Gold sequence
`0` (default) | integer scalar

Output variable-size signals — Option to output variable-length signals
`off` (default) | `on`

Maximum output size source — Maximum output size source
`Dialog parameter` (default) | `Inherit from reference port`

Maximum output size — Maximum output size
`[10 1]` (default) | vector of the form [n 1]

Sample time — Output sample time
`1` (default)

Samples per frame — Samples per frame
`1` (default) | positive integer

Reset on nonzero input — Reset output signal
`off` (default) | `on`

Output data type — Output data type
`double` (default) | `boolean` | `Smallest unsigned integer`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.