Channel Visualization

These channel modeling System objects and blocks in Communications Toolbox™ include an option to visualize the characteristics of a fading channel.

System object™	Block
`comm.MIMOChannel`	MIMO Fading Channel
`comm.RayleighChannel` and `comm.RicianChannel`	SISO Fading Channel

You can use the channel visualization option to view the impulse response and frequency response individually or side-by-side in one plot window. You can also view the Doppler spectrum. For more information about fading channels and the features available to model them, see Fading Channels.

Note

In the plot window, the displayed and specified path gain locations can differ by as much as 5% of the input sample time.
For MIMO channels, when the antenna selection property is set to any value other than Off and the specified transmit-receive pair is not selected for the current frame transmission, nothing will be displayed. Antenna selection is not applicable for SISO channels.
After you close channel visualization plots, the channel model executes at its normal speed.
Code generation is available only when the visualization property is set to Off.

Impulse Response Plot

The impulse response plot displays the path gains and the channel filter coefficients. The path gains occur at time instances that correspond to the specified path delays and might not align with the input sampling time. The implementations interpolate the channel filter coefficients from the actual path gains, use the coefficients to model the channel, and align the coefficients with the input sampling time. When the path gains align with the sampling time, they overlap the channel filter coefficients.

This plot shows the impulse response for a Rayleigh fading channel configured with path gains that align with the sample timing. The path gains overlap with the channel filter coefficients, and the coefficients are equally distributed.

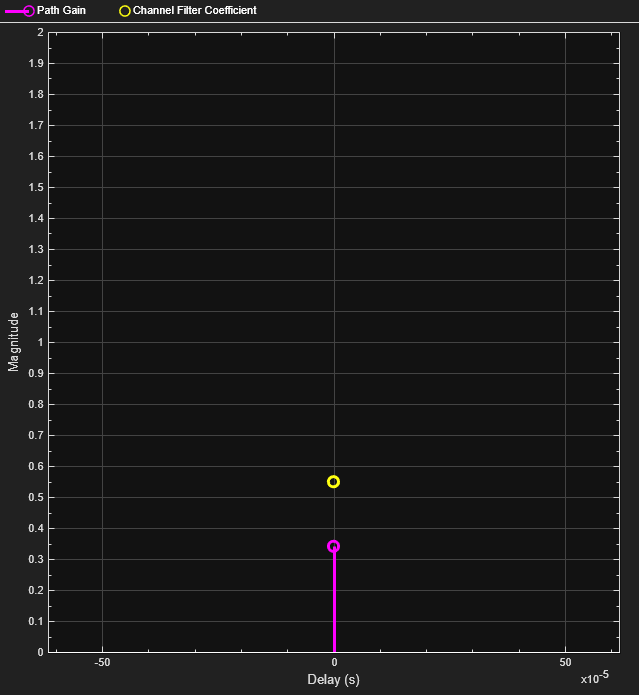
This plot shows the impulse response for a Rayleigh fading channel configured with path gains that do not align with the sample timing. The path gains do not overlap with the channel filter coefficients, but the coefficients are still equally distributed. The implementation oversamples the interpolation of the coefficients to faithfully reproduce the desired path gains.

The next plot shows the impulse response for a frequency-flat channel. A frequency-flat channel is represented by a single coefficient; no interpolation is required.

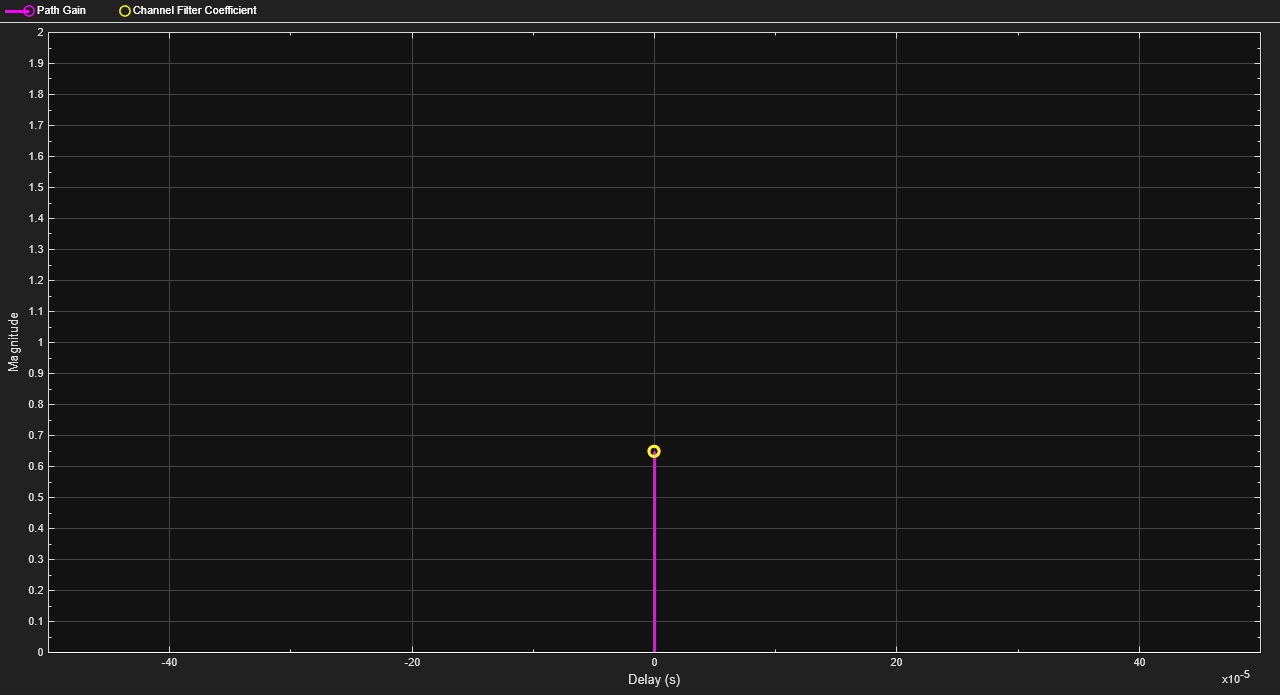
Frequency Response Plot

The frequency response plot displays the channel spectrum by taking a discrete Fourier transform of the channel filter coefficients. For the MIMO case, this transform is performed for the specified transmit-receive antenna pair. The default settings use a rectangular window. The window length is set according to the channel model configuration. The y-axis limits of the plot are computed based on the normalized and average path gain values.

This plot shows the frequency response plot for a frequency-selective channel.

Impulse and Frequency Responses Plot

The impulse and frequency responses plot displays the path gains and the channel filter coefficients in the left subplot and the frequency response in the right subplot.

This plot shows the impulse response and frequency response for a Rayleigh fading channel configured with path gains that align with the sample timing.

Doppler Spectrum Plot

The Doppler spectrum plot displays both the theoretical Doppler spectrum and the empirically determined data points. When the internal buffer is completely filled with filtered Gaussian samples, the empirical plot is updated. The empirical plot is the running mean of the spectrum calculated from each full buffer. The samples needed before the next update is displayed is a function of the sample rate and the maximum Doppler shift.

This plot shows a channel with Jakes Doppler spectrum.

For static channels, the Doppler spectrum reduces to a single point. The bottom toolbar of the plot window displays the message Reset fading channel for next update.

Channel Visualization Examples

Apply FSK Modulation in Various Fading Channels

Open Live Script

Pass an FSK signal through a Rayleigh multipath fading channel. Change the signal bandwidth to observe the impact of the fading channel on the FSK spectrum.

Flat Fading Channel

Set modulation order to 4, the modulated symbol rate to 45 bps, and the frequency separation to 200 Hz.

M = 4;           % Modulation order
symbolRate = 45; % Symbol rate (bps)
freqSep = 200;   % Frequency separation (Hz)

Calculate the samples per symbol parameter, sampPerSym, as a function of the modulation order, frequency separation, and symbol rate. To avoid output signal aliasing, the product of sampPerSym and symbolRate must be greater than the product of M and freqSep. Calculate the sample rate of the FSK output signal.

sampPerSym = ceil(M*freqSep/symbolRate);
fsamp = sampPerSym*symbolRate;

Create an FSK modulator.

fskMod = comm.FSKModulator(M, ...
    FrequencySeparation=freqSep, ...
    SamplesPerSymbol=sampPerSym, ...
    SymbolRate=symbolRate);

Set the path delays and average path gains for the three-path fading channel.

pathDelays = [0 3 10]*1e-6; % Discrete delays (s)
avgPathGains = [0 -3 -6];   % Average path gains (dB)

By convention, the delay of the first path is typically set to zero. For subsequent paths, a 1 microsecond delay corresponds to a 300 m difference in path length. The path delays and path gains specify the average delay profile of the channel.

Create a Rayleigh channel using the defined parameters. Set the Visualization property to display the impulse and frequency responses.

channel = comm.RayleighChannel( ...
    SampleRate=fsamp, ...
    PathDelays=pathDelays, ...
    AveragePathGains=avgPathGains, ...
    MaximumDopplerShift=0.01, ...
    Visualization='Impulse and frequency responses', ...
    SamplesToDisplay='10%');

Generate random data symbols and apply FSK modulation.

data = randi([0 3],2000,1);
modSig = fskMod(data);

Create a spectrum analyzer object to plot the FSK modulated signal and the received signal after flat fading channel filtering.

sa1 = spectrumAnalyzer( ...
    SampleRate=fsamp, ...
    ChannelNames=["FSK modulated signal", ...
        "Flat fading channel"]);

The modulated signal is composed of four tones, each having approximately 20 dBm peak power separated by 200 Hz.

Pass the signal through the Rayleigh fading channel and apply AWGN having a 25 dB signal-to-noise ratio.

snrdB = 25;
raylFadedData = channel(modSig);

rxSig = awgn(raylFadedData,snrdB);

The impulse and frequency responses show that the channel behaves as though it were flat. This flat response is because the signal bandwidth, 800 Hz, is much smaller than the coherence bandwidth, 50 kHz.

Plot the signal spectrum of the FSK-modulated signal before and after channel filtering. The four tones comprising the FSK signal maintain the same frequency separation and peak power levels relative to each other. The absolute peak power levels have decreased due to the fading channel.

sa1(modSig,rxSig)
release(sa1)

Frequency-Selective Fading

Increase the symbol rate to 45 kbps and the frequency separation to 200 kHz. Calculate the new samples per symbol and sample rate parameters. Release the FSK modulator object and update its configuration.

symbolRate = 45e3;
freqSep = 200e3;

release(fskMod)
fskMod.SymbolRate = symbolRate;
fskMod.FrequencySeparation = freqSep;

Create a spectrum analyzer object to plot the FSK modulated signal and the received signal after frequency-selective fading channel filtering.

sampPerSym = ceil(M*freqSep/symbolRate);
sa2 = spectrumAnalyzer( ...
    SampleRate=sampPerSym*symbolRate, ...
    ChannelNames=["FSK modulated signal", ...
        "Frequecy-selective fading channel"]);

Apply FSK modulation to the transmission data.

modSig = fskMod(data);

Release the channel object and update the channel sample rate property. Pass the signal through the Rayleigh fading channel and apply AWGN. The impulse and frequency responses show that the multipath fading is frequency selective.

release(channel)
fsamp = sampPerSym*symbolRate;
channel.SampleRate = fsamp;

rxSig = awgn(channel(modSig),25);

Plot the signal spectrum of the FSK-modulated signal before and after channel filtering. The spectrum has the same shape as in the flat-fading case, but the four tones are now separated by 200 kHz. There are still four identifiable tones, but their relative peak power levels differ due to the frequency-selective fading. The 800 kHz signal bandwidth is larger than the 50 kHz coherence bandwidth.

sa2(modSig,rxSig)
release(sa2)

QPSK Modulation in Fading Channel

Open Live Script

Pass a QPSK signal through a Rayleigh multipath fading channel. Change the signal bandwidth to observe the impact of the fading channel on the QPSK constellation.

QPSK Modulation in Flat Fading

Set the symbol rate parameter to 500 bps.

symbolRate = 500;

Generate random data symbols and apply QPSK modulation.

data = randi([0 3],10000,1);
modSig = pskmod(data,4,pi/4,'gray');

Set the path delays and average path gains for the fading channel.

pathDelays = [0 3 10]*1e-6; % Discrete delays of three-path channel (s)
avgPathGains = [0 -3 -6];   % Average path gains (dB)

By convention, the delay of the first path is typically set to zero. For subsequent paths, a 1 microsecond delay corresponds to a 300 meter difference in path length. The path delays and path gains specify the average delay profile of the channel.

Create a Rayleigh channel using the defined parameters. Set the Visualization property to display the impulse and frequency responses.

fsamp = symbolRate;
channel = comm.RayleighChannel( ...
    SampleRate=fsamp, ...
    PathDelays=pathDelays, ...
    AveragePathGains=avgPathGains, ...
    MaximumDopplerShift=0.01, ...
    Visualization="Impulse and frequency responses");

Pass the signal through the Rayleigh channel and apply AWGN.

rxSig = awgn(channel(modSig),25);

The impulse and frequency responses show that the channel behaves as though it were flat. This is because the signal bandwidth, 500 Hz, is much smaller than the coherence bandwidth, 50 kHz. Alternatively, the delay span of the channel (10 microseconds) is much smaller than the QPSK symbol period (2 milliseconds) so the resultant bandlimited impulse response is approximately flat.

Plot the constellation.

constDiagram = comm.ConstellationDiagram;
constDiagram(rxSig)

The QPSK constellation shows the effects of the fading channel; however, the signal still has four identifiable states.

QPSK Modulation in Frequency-Selective Fading

Increase the symbol rate to 500 kbps and update the related channel property. Pass the signal through the Rayleigh channel and apply AWGN.

symbolRate = 500e3;

release(channel)
channel.SampleRate = symbolRate;

rxSig = awgn(channel(modSig),25);

The impulse and frequency responses show that the multipath fading is frequency selective.

Plot the constellation.

constDiagram(rxSig)

As the signal bandwidth is increased from 500 Hz to 500 kHz, the signal becomes highly distorted. This distortion is due to the intersymbol interference (ISI) that comes from time dispersion of the wideband signal. The delay span of the channel (10 microseconds) is now larger than the QPSK symbol period (2 microseconds) so the resultant bandlimited impulse response is no longer flat. Alternatively, the signal bandwidth is much larger than the coherence bandwidth, 50 kHz.