MIMO Fading Channel

Filter input signal through MIMO multipath fading channel

Libraries:
Communications Toolbox / Channels
Communications Toolbox / MIMO

Description

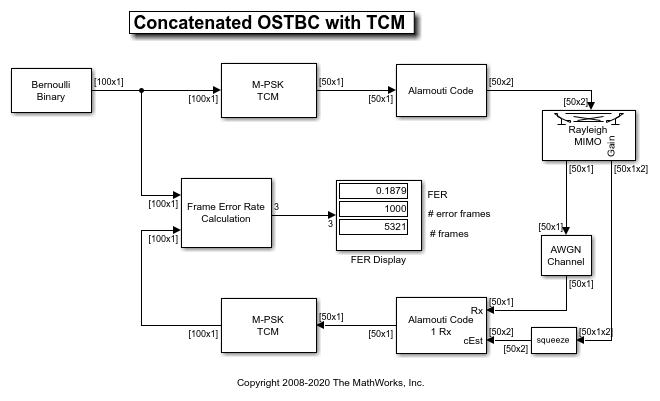
The MIMO Fading Channel block filters an input signal using a multi-input/multi-output (MIMO) multipath fading channel. This block models both Rayleigh and Rician fading and employs the Kronecker model for modeling the spatial correlation between the links. For processing details, see the Algorithms section.

Signal Dimensions

The availability and dimensions of input and output port signals depends on:

The Antenna selection parameter setting on the Main tab
The Initial time source parameter setting on the Realization tab
The Output channel path gains selection on the Realization tab

Antenna Selection Parameter	Signal Input (in)	Transmit Selection Input (Tx Sel)	Receive Selection Input (Rx Sel)	Initial Time Offset Input (Init Time)	Signal Output (Out1)	Optional Channel Gain Output (Gain)
`Off`	N_S-by-N_T	N/A	N/A	nonnegative scalar	N_S-by-N_R	N_S-by-N_P-by-N_T-by-N_R
`Tx`	N_S-by-N_ST	1-by-N_T	N/A		N_S-by-N_R
`Rx`	N_S-by-N_T	N/A	1-by-N_R		N_S-by-N_SR
`Tx and Rx`	N_S-by-N_ST	1-by-N_T	1-by-N_R		N_S-by-N_SR

N_S represents the number of samples in the input signal.
N_T represents the number of transmit antennas, as determined by:
- Transmit spatial correlation when you set Specify spatial correlation to Separate Tx Rx
- Number of transmit antennas when you set Specify spatial correlation to None or Combined
N_R represents the number of receive antennas, as determined by:
- Receive spatial correlation when you set Specify spatial correlation to Separate Tx Rx
- Number of receive antennas when you set Specify spatial correlation to None
- Combined spatial correlation and Number of transmit antennas when you set Specify spatial correlation to Combined
N_P represents the number of channel paths, as determined by the Discrete path delays (s) or Average path gains (dB).
N_ST represents the number of selected transmit antennas, as determined by the number of elements set to 1 in the vector provided to the Tx Sel input port.
N_SR represents the number of selected receive antennas, as determined by the number of elements set to 1 in the vector provided to the Rx Sel input port.

Examples

Concatenated OSTBC with TCM in Simulink

Model orthogonal space-time block code concatenated with trellis-coded modulation for information transmission over a 2-by-1 MIMO channel in Simulink^®.

Open Model

Ports

Input

expand all

in — Input data signal
vector

Input data signal, specified as an N_S-by-N_T or N_S-by-N_ST matrix.

N_S represents the number of samples in the input signal.
N_T represents the number of transmit antennas.
N_ST represents the number of selected transmit antennas.

Data Types: double | single
Complex Number Support: Yes

Tx Sel — Select active transmit antennas
binary vector

Select active transmit antennas, specified as a 1-by-N_T binary vector. N_T represents the number of transmit antennas. Elements set to 1 identify selected antenna indices and 0 identify nonselected antenna indices.

Dependencies

To enable this port, on the Main tab, set Antenna selection to Tx or Tx and Rx.

Data Types: double

Rx Sel — Select active receive antennas
binary vector

Select active receive antennas, specified as a 1-by-N_R binary vector. N_R represents the number of receive antennas. Elements set to 1 identify selected antenna indices and 0 identify nonselected antenna indices.

Dependencies

To enable this port, on the Main tab, set Antenna selection to Rx or Tx and Rx.

Data Types: double

Init Time — Initial time offset
nonnegative scalar

Initial time offset for the fading model in seconds, specified as a nonnegative scalar.

Init Time must be greater than the last frame end time. When Init Time is not a multiple of 1/Sample Rate (Hz), it is rounded up to the nearest sample position.

Dependencies

To enable this port, on the Realization tab, set Initial time source to Input port.

Data Types: double

Output

expand all

Out1 — Output data signal for fading channel
vector

Output data signal for the fading channel, returned as an N_S-by-N_R or N_S-by-N_SR matrix.

N_S represents the number of samples in the input signal.
N_R represents the number of receive antennas.
N_SR represents the number of selected receive antennas.

Gain — Discrete path gains
4-D array

Discrete path gains of the underlying fading process, returned as an N_S-by-N_P-by-N_T-by-N_R array.

N_S represents the number of samples in the input signal.
N_P represents the number of channel paths.
N_T represents the number of transmit antennas.
N_R represents the number of receive antennas.

Entries for nonselected paths are filled with NaN.

Dependencies

To enable this port, on the Realization tab, select Output channel path gains.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Main Tab

Multipath parameters (frequency selectivity)

Inherit sample rate from input — Option to inherit the sample rate from input
on (default) | off

Select this parameter to use the sample rate of the input signal when processing. When you select Inherit sample rate from input, the sample rate is N_S/T_S. N_S is the number of input samples, and T_S is the model sample time.

Sample rate (Hz) — Input signal sample rate
`1` (default) | positive scalar

Input signal sample rate, specified in hertz as a positive scalar. To match the model settings, set the sample rate to N_S/T_S, where N_S is the number of input samples, and T_S is the model sample time.

Dependencies

This parameter appears when Inherit sample rate from input is not selected.

Discrete path delays (s) — Delays for each discrete path
`0` (default) | nonnegative scalar | row vector

Delays for each discrete path in seconds, specified as a nonnegative scalar or row vector.

When you set Discrete path delays (s) to a scalar, the MIMO channel is frequency flat.
When you set Discrete path delays (s) to a vector, the MIMO channel is frequency selective.

Average path gains (dB) — Average gain for each discrete path
`0` (default) | scalar | row vector

Average gain for each discrete path in decibels, specified as a scalar or row vector. Average path gains (dB) must have the same size as Discrete path delays (s).

Normalize average path gains to 0 dB — Option to normalize average path gains to 0 dB
on (default) | off

Select this parameter to normalize the fading processes so that the total power of the path gains, averaged over time, is 0 dB.

Fading distribution — Fading distribution of channel
`Rayleigh` (default) | `Rician`

Select the fading distribution of the channel, either Rayleigh or Rician.

K-factors — K-factor of Rician fading channel
`3` (default) | positive scalar | row vector of nonnegative values

K-factor of a Rician fading channel, specified as a positive scalar or a 1-by-N_P vector of nonnegative values. N_P equals the value of the Discrete path delays (s) parameter.

If you set K-factors to a scalar, the first discrete path is a Rician fading process with a Rician K-factor of K-factors. Any remaining discrete paths are independent Rayleigh fading processes.
If you set K-factors to a row vector, the discrete path corresponding to a positive element of the K-factors vector is a Rician fading process with a Rician K-factor specified by that element. The discrete path corresponding to any zero-valued elements of the K-factors vector are Rayleigh fading processes. At least one element value must be nonzero.

Dependencies

This parameter appears when you set Fading distribution to Rician.

LOS path Doppler shifts (Hz) — Doppler shifts for line-of-sight components
`0` (default) | scalar | row vector

Doppler shifts for the line-of-sight components of the Rician fading channel in hertz, specified as a scalar or row vector. This parameter must have the same size as K-factors.

If you set LOS path Doppler shifts (Hz) to a scalar, it represents the line-of-sight component Doppler shift of the first discrete path that is a Rician fading process.
If you set LOS path Doppler shifts (Hz) to a row vector, the discrete path that is a Rician fading process has its line-of-sight component Doppler shift specified by the elements of LOS path Doppler shifts (Hz) that correspond to positive elements in the K-factors vector.

Dependencies

This parameter appears when you set Fading distribution to Rician.

LOS path initial phases (rad) — Initial phases for line-of-sight components
`0` (default) | scalar | row vector

Initial phases for the line-of-sight component of the Rician fading channel in radians, specified as a scalar or row vector. This parameter must have the same size as K-factors.

If you set LOS path initial phases (rad) to a scalar, it is the line-of-sight component initial phase of the first discrete path that is a Rician fading process.
If you set LOS path initial phases (rad) to a row vector, the discrete path that is a Rician fading process has its line-of-sight component initial phase specified by the elements of LOS path initial phases (rad) that correspond to positive elements in the K-factors vector.

Dependencies

This parameter appears when you set Fading distribution to Rician.

Doppler parameters (time dispersion)

Maximum Doppler shift (Hz) — Maximum Doppler shift for all channel paths
`0.001` (default) | nonnegative scalar

Maximum Doppler shift for all channel paths in hertz, specified as a nonnegative scalar.

Maximum Doppler shift (Hz) must be less than or equal to (Sample Rate (Hz)/10)/f_c for each path, where f_c is the cutoff frequency factor of the path. For more information, see Cutoff Frequency Factor.

Doppler spectrum — Doppler spectrum shape for all channel paths
`doppler('Jakes')` (default) | `doppler('Flat')` | `doppler('Rounded', ...)` | `doppler('Bell', ...)` | `doppler('Asymmetric Jakes', ...)` | `doppler('Restricted Jakes', ...)` | `doppler('Gaussian', ...)` | `doppler('BiGaussian', ...)`

Doppler spectrum shape for all channel paths, specified as a single Doppler spectrum structure returned from the doppler function or a 1-by-N_P cell array of such structures. The default value of this parameter is the Jakes Doppler spectrum (doppler('Jakes')).

If you assign a single call to doppler, all paths have the same specified Doppler spectrum.
If you assign a 1-by-N_P cell array of calls to doppler using any of the specified syntaxes, each path has the Doppler spectrum specified by the corresponding Doppler spectrum structure in the array. In this case, N_P equals the value of the Discrete path delays (s) parameter.

Dependencies

This parameter applies when Maximum Doppler shift (Hz) is greater than zero.

If you set Technique for generating fading samples to Sum of sinusoids, Doppler spectrum must be doppler('Jakes').

Antenna parameters (spatial dispersion)

Specify spatial correlation — Spatial correlation mode
`None` (default) | `Separate Tx Rx` | `Combined`

Select the spatial correlation mode: None, Separate Tx Rx, or Combined.

Choose 'None' to specify the number of transmit and receive antennas.
Choose 'Spatial Tx Rx' to specify the transmit and receive spatial correlation matrices separately. The number of transmit (N_T) and receive (N_R) antennas are derived from the dimensions of the Transmit spatial correlation and Receive spatial correlation parameters, respectively.
Choose 'Combined' to specify a single correlation matrix for the whole channel. The product of N_T and N_R is derived from the dimension of Combined spatial correlation.

Number of transmit antennas — Number of transmit antennas
`2` (default) | positive integer

Number of transmit antennas, specified as a positive integer.

Dependencies

This parameter appears when you set Specify spatial correlation to None or Combined.

Number of receive antennas — Number of receive antennas
`2` (default) | positive integer

Number of receive antennas, specified as a positive integer.

Dependencies

This parameter appears when you set Specify spatial correlation to None.

Transmit spatial correlation — Spatial correlation of transmitter
`[1 0; 0 1]` (default) | matrix | 3-D array

Specify the spatial correlation of the transmitter as an N_T-by-N_T matrix or N_T-by-N_T-by-N_P array of complex or real values. N_T is the number of transmit antennas, and N_P equals the value of the Discrete path delays (s) parameter.

If you set Discrete path delays (s) to a scalar, the channel is frequency flat, and Transmit spatial correlation is an N_T-by-N_T Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.
If you set Discrete path delays (s) to a vector, the channel is frequency selective, and you can specify Transmit spatial correlation as a matrix. Each path has the same transmit spatial correlation matrix.
Alternatively, you can specify Transmit spatial correlation as an N_T-by-N_T-by-N_P array, where each path can have its own different transmit spatial correlation matrix.

Dependencies

This parameter appears when you set Specify spatial correlation to Separate Tx Rx.

Receive spatial correlation — Spatial correlation of receiver
`[1 0; 0 1]` (default) | matrix | 3-D array

Specify the spatial correlation of the receiver as an N_R-by-N_R matrix or N_R-by-N_R-by-N_P array of complex or real values. N_R is the number of receive antennas, and N_P equals the value of the Discrete path delays (s) parameter.

If you set Discrete path delays (s) to a scalar, the channel is frequency flat, and Receive spatial correlation is an N_R-by-N_R Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.
If you set Discrete path delays (s) to a vector, the channel is frequency selective, and you can specify Receive spatial correlation as a matrix. Each path has the same receive spatial correlation matrix.
Alternatively, you can specify Receive spatial correlation as an N_R-by-N_R-by-N_P array, where each path can have its own different receive spatial correlation matrix.

Dependencies

This parameter appears when you set Specify spatial correlation to Separate Tx Rx.

Combined spatial correlation — Combined spatial correlation matrix
`[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]` (default) | matrix | 3-D array

Specify the combined spatial correlation matrix as an N_TR-by-N_TR matrix or N_TR-by-N_TR-by-N_P array of complex or real values. N_TR = (N_T ✕ N_R), and N_P equals the number of delay paths specified by the Discrete path delays (s) parameter.

If you set Discrete path delays (s) to a scalar, the channel is frequency flat, and Combined spatial correlation is an N_TR-by-N_TR Hermitian matrix. The magnitude of any off-diagonal element must be no larger than the geometric mean of the two corresponding diagonal elements.
If you set Discrete path delays (s) to a vector, the channel is frequency selective, and you can specify Combined spatial correlation as a matrix. Each path has the same spatial correlation matrix.
Alternatively, you can specify Combined spatial correlation as an N_TR-by-N_TR-by-N_P array, where each path can have its own different combined spatial correlation matrix.

Dependencies

This parameter appears when you set Specify spatial correlation to Combined.

Normalize outputs by number of receive antennas — Normalize channel output
on (default) | off

Select this parameter to normalize the channel outputs by the number of receive antennas.

Simulate using — Compilation type
`Interpreted execution` (default) | `Code generation`

Compilation type, specified as Interpreted execution or Code generation.

Antenna selection — Antenna mode
`Off` (default) | `Tx` | `Rx` | `Tx and Rx`

The antenna mode you select corresponds to additional input ports on the block.

Antenna selection Setting	Input Ports Added
`Off`	None
`Tx`	Tx Sel
`Rx`	Rx Sel
`Tx and Rx`	Tx Sel, Rx Sel

Realization Tab

Technique for generating fading samples — Channel modeling technique
`Filtered Gaussian noise` (default) | `Sum of sinusoids`

Select the channel modeling technique, either Filtered Gaussian noise or Sum of sinusoids.

Number of sinusoids — Number of sinusoids used
`48` (default) | positive integer

Number of sinusoids used to model the fading process, specified as a positive integer.

Dependencies

This parameter appears when you set Technique for generating fading samples to Sum of sinusoids.

Initial time source — Source of initial time offset
`Property` (default) | `Input port`

Indicate the source of the initial time offset for the fading model, either Property or Input port.

When you set Initial time source to Property, use Initial time (s) to set the initial time offset.
When you set Initial time source to Input port, use the input port Init Time to set the initial time offset.

Dependencies

This parameter appears when you set Technique for generating fading samples to Sum of sinusoids.

Initial time (s) — Initial time offset
`0` (default) | nonnegative scalar

Initial time offset for the fading model, specified as a nonnegative scalar.

When Initial time (s) is not a multiple of 1/Sample Rate (Hz), it is rounded up to the nearest sample position.

Dependencies

This parameter appears when you set Technique for generating fading samples to Sum of sinusoids and Initial time source to Property.

Initial seed — Random number generator initial seed
`73` (default) | nonnegative integer

Random number generator initial seed for this block, specified as a nonnegative integer.

Output channel path gains — Option to output channel path gains
off (default) | on

Select this parameter to add the Gain output port to the block and output the channel path gains of the underlying fading process.

Visualization Tab

Channel visualization — Select the channel visualization
`Off` (default) | `Impulse response` | `Frequency response` | `Doppler spectrum` | `Impulse and frequency responses`

Select the channel visualization: Off, Impulse response, Frequency response, Doppler spectrum, or Impulse and frequency responses. When visualization is on, the selected channel characteristics, such as impulse response or Doppler spectrum, display in a separate window. For more information, see Channel Visualization.

Antenna pair to display — Transmit-receive antenna pair to display
`[1,1]` (default) | vector

Transmit-receive antenna pair to display, specified as a 1-by-2 vector, where the first element corresponds to the desired transmit antenna and the second corresponds to the desired receive antenna. At this time, only a single pair can be displayed.

Dependencies

This parameter appears when Channel visualization is not Off.

Percentage of samples to display — Percentage of samples to display
`25%` (default) | `10%` | `50%` | `100%`

Select the percentage of samples to display: 10%, 25%, 50%, or 100%. Increasing the percentage improves display accuracy at the expense of simulation speed.

Dependencies

This parameter appears when you set Channel visualization to Impulse response, Frequency response, or Impulse and frequency responses.

Path for Doppler spectrum display — Path for which Doppler spectrum is displayed
`1` (default) | positive integer

Path for which the Doppler spectrum is displayed, specified as a positive integer from 1 to N_P, where N_P equals the value of the Discrete path delays (s) parameter.

Dependencies

This parameter appears when you set Channel visualization to Doppler spectrum.

Block Characteristics

Data Types	`double` \| `single`
Multidimensional Signals	`yes`
Variable-Size Signals	`yes`

Algorithms

expand all

The fading processing per link is described in Methodology for Simulating Multipath Fading Channels and assumes the same parameters for all (N_T × N_R) links of the MIMO channel. Each link comprises all multipaths for that link.

The Kronecker Model

The Kronecker model assumes that the spatial correlations at the transmit and receive sides are separable. Equivalently, the direction of departure (DoD) and directions of arrival (DoA) spectra are assumed to be separable. The full correlation matrix is:

$R_{H} = E [R_{t} \otimes R_{r}]$

The ⊗ symbol represents the Kronecker product.
R_t is the correlation matrix at the transmit side, $R_{t} = E [H^{H} H]$ , and is of size N_T-by-N_T.
R_r is the correlation matrix at the receive side, $R_{r} = E [H H^{H}]$ , and is of size N_R-by-N_R.

You can obtain a realization of the MIMO channel matrix as:

$H = R_{r}^{\frac{1}{2}} A R_{t}^{\frac{1}{2}}$

A is an N_R-by-N_T matrix of independent identically distributed complex Gaussian variables with zero mean and unit variance.

Cutoff Frequency Factor

The cutoff frequency factor, f_c, is dependent on the type of Doppler spectrum.

For any Doppler spectrum type other than Gaussian and bi-Gaussian, f_c equals 1.
For a doppler('Gaussian') spectrum type, f_c equals NormalizedStandardDeviation $\times \sqrt{2 \log 2}$ .
For a doppler('BiGaussian') spectrum type:
- If the PowerGains(1) and NormalizedCenterFrequencies(2) field values are both 0, then f_c equals NormalizedStandardDeviation(1) $\times \sqrt{2 \log 2}$ .
- If the PowerGains(2) and NormalizedCenterFrequencies(1) field values are both 0, then f_c equals NormalizedStandardDeviation(2) $\times \sqrt{2 \log 2}$ .
- If the NormalizedCenterFrequencies field value is [0,0] and the NormalizedStandardDeviation field has two identical elements, then f_c equals NormalizedStandardDeviation(1) $\times \sqrt{2 \log 2}$ .
- In all other cases, f_c equals 1.

Antenna Selection

When the object is in antenna-selection mode, it uses these algorithms to process an input signal.

All random path gains are always generated and keep evolving for each link, whether or not a given link is selected. The path gain values output for the nonselected links are populated with NaN.
The spatial correlation applies to only the selected transmit and receive antennas, and the correlation coefficients are the corresponding entries in the transmit, receive, or combined correlation matrices. That is, the spatial correlation matrix for the selected transmit or receive antennas is a submatrix of the transmit, receive, or combined spatial correlation matrix property value.
For signal paths that are associated with nonactive antennas, a signal with zero power is transmitted to the channel filter.
Channel output normalization happens over the number of selected receive antennas.

References

[1] Oestges, C., and B. Clerckx. MIMO Wireless Communications: From Real-World Propagation to Space-Time Code Design. Academic Press, 2007.

[2] Correira, L. M. Mobile Broadband Multimedia Networks: Techniques, Models and Tools for 4G. Academic Press, 2006.

[3] Kermoal, J. P., L. Schumacher, K. I. Pedersen, P. E. Mogensen, and F. Frederiksen. "A stochastic MIMO radio channel model with experimental validation." IEEE Journal on Selected Areas of Communications. Vol. 20, Number 6, 2002, pp. 1211–1226.

[4] Jeruchim, M., P. Balaban, and K. S. Shanmugan. Simulation of Communication Systems. Second Edition. New York: Kluwer Academic/Plenum, 2000.

[5] Pätzold, Matthias, Cheng-Xiang Wang, and Bjorn Olav Hogstand. "Two New Sum-of-Sinusoids-Based Methods for the Efficient Generation of Multiple Uncorrelated Rayleigh Fading Waveforms." IEEE Transactions on Wireless Communications. Vol. 8, Number 6, 2009, pp. 3122–3131.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2013b

expand all

R2022b: Updates to channel visualization display

The channel visualization feature now presents:

Configuration settings in the bottom toolbar on the plot window.
Plots side-by-side in one window when you select the Impulse and frequency response channel visualization option.

MIMO Fading Channel

Description

Signal Dimensions

Examples

Concatenated OSTBC with TCM in Simulink

Ports

Input

in — Input data signal vector

Tx Sel — Select active transmit antennas binary vector

Dependencies

Rx Sel — Select active receive antennas binary vector

Dependencies

Init Time — Initial time offset nonnegative scalar

Dependencies

Output

Out1 — Output data signal for fading channel vector

Gain — Discrete path gains 4-D array

Dependencies

Parameters

Main Tab

Inherit sample rate from input — Option to inherit the sample rate from input on (default) | off

Sample rate (Hz) — Input signal sample rate 1 (default) | positive scalar

Dependencies

Discrete path delays (s) — Delays for each discrete path 0 (default) | nonnegative scalar | row vector

Average path gains (dB) — Average gain for each discrete path 0 (default) | scalar | row vector

Normalize average path gains to 0 dB — Option to normalize average path gains to 0 dB on (default) | off

Fading distribution — Fading distribution of channel Rayleigh (default) | Rician

K-factors — K-factor of Rician fading channel 3 (default) | positive scalar | row vector of nonnegative values

Dependencies

LOS path Doppler shifts (Hz) — Doppler shifts for line-of-sight components 0 (default) | scalar | row vector

Dependencies

LOS path initial phases (rad) — Initial phases for line-of-sight components 0 (default) | scalar | row vector

Dependencies

Maximum Doppler shift (Hz) — Maximum Doppler shift for all channel paths 0.001 (default) | nonnegative scalar

Doppler spectrum — Doppler spectrum shape for all channel paths doppler('Jakes') (default) | doppler('Flat') | doppler('Rounded', ...) | doppler('Bell', ...) | doppler('Asymmetric Jakes', ...) | doppler('Restricted Jakes', ...) | doppler('Gaussian', ...) | doppler('BiGaussian', ...)

Dependencies

Specify spatial correlation — Spatial correlation mode None (default) | Separate Tx Rx | Combined

Number of transmit antennas — Number of transmit antennas 2 (default) | positive integer

Dependencies

Number of receive antennas — Number of receive antennas 2 (default) | positive integer

Dependencies

Transmit spatial correlation — Spatial correlation of transmitter [1 0; 0 1] (default) | matrix | 3-D array

Dependencies

Receive spatial correlation — Spatial correlation of receiver [1 0; 0 1] (default) | matrix | 3-D array

Dependencies

Combined spatial correlation — Combined spatial correlation matrix [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1] (default) | matrix | 3-D array

Dependencies

Normalize outputs by number of receive antennas — Normalize channel output on (default) | off

Simulate using — Compilation type Interpreted execution (default) | Code generation

Antenna selection — Antenna mode Off (default) | Tx | Rx | Tx and Rx

Realization Tab

Technique for generating fading samples — Channel modeling technique Filtered Gaussian noise (default) | Sum of sinusoids

Number of sinusoids — Number of sinusoids used 48 (default) | positive integer

Dependencies

Initial time source — Source of initial time offset Property (default) | Input port

Dependencies

Initial time (s) — Initial time offset 0 (default) | nonnegative scalar

Dependencies

Initial seed — Random number generator initial seed 73 (default) | nonnegative integer

Output channel path gains — Option to output channel path gains off (default) | on

Visualization Tab

Channel visualization — Select the channel visualization Off (default) | Impulse response | Frequency response | Doppler spectrum | Impulse and frequency responses

Antenna pair to display — Transmit-receive antenna pair to display [1,1] (default) | vector

Dependencies

Percentage of samples to display — Percentage of samples to display 25% (default) | 10% | 50% | 100%

Dependencies

Path for Doppler spectrum display — Path for which Doppler spectrum is displayed 1 (default) | positive integer

Dependencies

Block Characteristics

Algorithms

The Kronecker Model

Cutoff Frequency Factor

Antenna Selection

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2022b: Updates to channel visualization display

See Also

Blocks

in — Input data signal
vector

Tx Sel — Select active transmit antennas
binary vector

Rx Sel — Select active receive antennas
binary vector

Init Time — Initial time offset
nonnegative scalar

Out1 — Output data signal for fading channel
vector

Gain — Discrete path gains
4-D array

Inherit sample rate from input — Option to inherit the sample rate from input
on (default) | off

Sample rate (Hz) — Input signal sample rate
`1` (default) | positive scalar

Discrete path delays (s) — Delays for each discrete path
`0` (default) | nonnegative scalar | row vector

Average path gains (dB) — Average gain for each discrete path
`0` (default) | scalar | row vector

Normalize average path gains to 0 dB — Option to normalize average path gains to 0 dB
on (default) | off

Fading distribution — Fading distribution of channel
`Rayleigh` (default) | `Rician`

K-factors — K-factor of Rician fading channel
`3` (default) | positive scalar | row vector of nonnegative values

LOS path Doppler shifts (Hz) — Doppler shifts for line-of-sight components
`0` (default) | scalar | row vector

LOS path initial phases (rad) — Initial phases for line-of-sight components
`0` (default) | scalar | row vector

Maximum Doppler shift (Hz) — Maximum Doppler shift for all channel paths
`0.001` (default) | nonnegative scalar

Specify spatial correlation — Spatial correlation mode
`None` (default) | `Separate Tx Rx` | `Combined`

Number of transmit antennas — Number of transmit antennas
`2` (default) | positive integer

Number of receive antennas — Number of receive antennas
`2` (default) | positive integer

Transmit spatial correlation — Spatial correlation of transmitter
`[1 0; 0 1]` (default) | matrix | 3-D array

Receive spatial correlation — Spatial correlation of receiver
`[1 0; 0 1]` (default) | matrix | 3-D array

Combined spatial correlation — Combined spatial correlation matrix
`[1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1]` (default) | matrix | 3-D array

Normalize outputs by number of receive antennas — Normalize channel output
on (default) | off

Simulate using — Compilation type
`Interpreted execution` (default) | `Code generation`

Antenna selection — Antenna mode
`Off` (default) | `Tx` | `Rx` | `Tx and Rx`

Technique for generating fading samples — Channel modeling technique
`Filtered Gaussian noise` (default) | `Sum of sinusoids`

Number of sinusoids — Number of sinusoids used
`48` (default) | positive integer

Initial time source — Source of initial time offset
`Property` (default) | `Input port`

Initial time (s) — Initial time offset
`0` (default) | nonnegative scalar

Initial seed — Random number generator initial seed
`73` (default) | nonnegative integer

Output channel path gains — Option to output channel path gains
off (default) | on

Channel visualization — Select the channel visualization
`Off` (default) | `Impulse response` | `Frequency response` | `Doppler spectrum` | `Impulse and frequency responses`

Antenna pair to display — Transmit-receive antenna pair to display
`[1,1]` (default) | vector

Percentage of samples to display — Percentage of samples to display
`25%` (default) | `10%` | `50%` | `100%`

Path for Doppler spectrum display — Path for which Doppler spectrum is displayed
`1` (default) | positive integer

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.