AWGN Channel
Add white Gaussian noise to input signal
Libraries:
Communications Toolbox /
Channels
Description
The AWGN Channel block adds white Gaussian noise to the input signal. It inherits the sample time from the input signal.
Examples
When your simulation uses coding, the Eb/N0 setting for the AWGN channel must be adjusted by the coding rate to apply the desired signal to noise (SNR) ratio.
The slex_hamming_check.slx model performs forward error correction (FEC) coding on a BPSK-modulated signal that gets filtered through an AWGN channel. The model uses BPSK Modulator Baseband, AWGN Channel, and BPSK Demodulator Baseband discrete blocks to simulate a binary symmetric channel. To account for difference between the coded and uncoded Eb/N0 (Eb/N0), the AWGN channel block computes the coded Eb/N0 as Eb/N0 + 10log10(K/N) dB, where K/N is the code rate and Eb/N0 is the uncoded Eb/N0. The Hamming Encoder block has an input bit period of 1 second and the output bit period decreases, by a factor of the K/N code rate, to 4/7 seconds. Due to the coding rate, the Binary Symmetric Channel has a bit period of 4/7 seconds.
The model initializes variables used to configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink).
model = 'slex_hamming_check';
open_system(model);
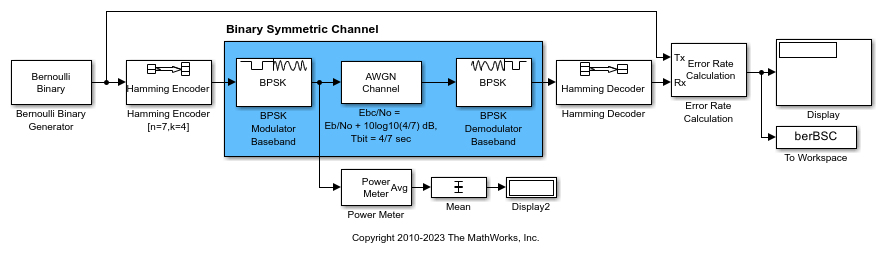
The AWGN channel block must also configure the Number of bits per symbol and Input signal power, referenced to 1 ohm (watts) parameter settings based on the modulated signal. This example uses BPSK modulation, so the AWGN Channel block has number of bits per symbol set to 1. The model includes a Power Meter block that measures the signal power at the AWGN input to confirm the setting required for the input signal power of the AWGN Channel block.
Produce error rate results and a plot to compare simulation with theory. The theoretical channel error probability for the coded signal is Q(sqrt(2*Ebc/N0)), where Q() is the standard Q function and Ebc/N0 is the coded Eb/N0 in linear units (not in dB). Compute the theoretical BER upper limit bound of a linear, rate 4/7 block code with a minimum distance of 3, and hard decision decoding for a BPSK-modulated signal in AWGN over a range of Eb/N0 values by using the bercodingslex_hamming_check model over the same range of Eb/N0 values.
EbNoVec = 0:2:10; theorBER = bercoding(EbNoVec,'block','hard',7,4,3); berVecBSC = zeros(length(EbNoVec),3); for n = 1:length(EbNoVec) EbNo = EbNoVec(n); sim(model); berVecBSC(n,:) = berBSC(end,1); end
Plot the results by using the semilogy function to show the nearly identical results. The model has the Error Rate Calculation block configured to run each Eb/N0 point until 200 errors occur or the block receives 1x10^6 bits.
semilogy( ... EbNoVec,berVecBSC(:,1),'d', ... EbNoVec,theorBER,'-'); legend('BSC BER','Theoretical BER', ... Location="southwest"); xlabel("Eb/N0 (dB)"); ylabel("Error Probability"); title("Bit Error Probability"); grid on;

This model shows the improvement in BER performance when using log-likelihood ratio (LLR) instead of hard decision demodulation in a convolutionally coded communication link.
For a MATLAB® version of this example, see Log-Likelihood Ratio (LLR) Demodulation.
System Setup
This example model simulates a convolutionally coded communication system having one transmitter, an AWGN channel and three receivers. The convolutional encoder has a code rate of 1/2. The system employs a 16-QAM modulation. The modulated signal passes through an additive white Gaussian noise channel. The top receiver performs hard decision demodulation in conjunction with a Viterbi decoder that is set up to perform hard decision decoding. The second receiver has the demodulator configured to compute log-likelihood ratios (LLRs) that are then quantized using a 3-bit quantizer. It is well known that the quantization levels are dependent on noise variance for optimum performance [2]. The exact boundaries of the quantizer are empirically determined here. A Viterbi decoder that is set up for soft decision decoding processes these quantized values. The LLR values computed by the demodulator are multiplied by -1 to map them to the right quantizer index for use with Viterbi Decoder. To compute the LLR, the demodulator must be given the variance of noise as seen at its input. The third receiver includes a demodulator that computes LLRs which are processed by a Viterbi decoder that is set up in unquantized mode. The BER performance of each receiver is computed and displayed.
modelName = 'commLLRvsHD';
open_system(modelName);
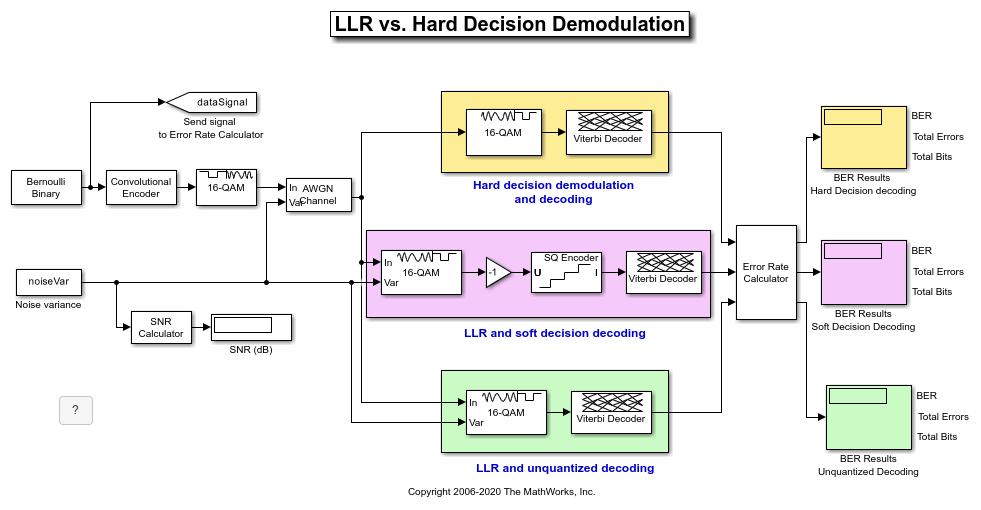
System Simulation and Visualization
Simulate this system over a range of information bit Eb/No values. Adjust these Eb/No values for coded bits and multi-bit symbols to get noise variance values required for the AWGN block and Rectangular QAM Baseband Demodulator block. Collect BER results for each Eb/No value and visualize the results.
EbNo = 2:0.5:8; % information rate Eb/No in dB codeRate = 1/2; % code rate of convolutional encoder nBits = 4; % number of bits in a 16-QAM symbol Pavg = 10; % average signal power of a 16-QAM modulated signal snr = EbNo - 10*log10(1/codeRate) + 10*log10(nBits); % SNR in dB noiseVarVector = Pavg ./ (10.^(snr./10)); % noise variance % Initialize variables for storing the BER results ber_HD = zeros(1,length(EbNo)); ber_SD = zeros(1,length(EbNo)); ber_LLR = zeros(1, length(EbNo)); % Loop over all noiseVarVector values for idx=1:length(noiseVarVector) noiseVar = noiseVarVector(idx); %#ok<NASGU> sim(modelName); % Collect BER results ber_HD(idx) = BER_HD(1); ber_SD(idx) = BER_SD(1); ber_LLR(idx) = BER_LLR(1); end % Perform curve fitting and plot the results fitBER_HD = real(berfit(EbNo,ber_HD)); fitBER_SD = real(berfit(EbNo,ber_SD)); fitBER_LLR = real(berfit(EbNo,ber_LLR)); semilogy(EbNo,ber_HD,'r*', ... EbNo,ber_SD,'g*', ... EbNo,ber_LLR,'b*', ... EbNo,fitBER_HD,'r', ... EbNo,fitBER_SD,'g', ... EbNo,fitBER_LLR,'b'); legend('Hard Decision Decoding', ... 'Soft Decision Decoding','Unquantized Decoding'); xlabel('Eb/No (dB)'); ylabel('BER'); title('LLR vs. Hard Decision Demodulation with Viterbi Decoding'); grid on;
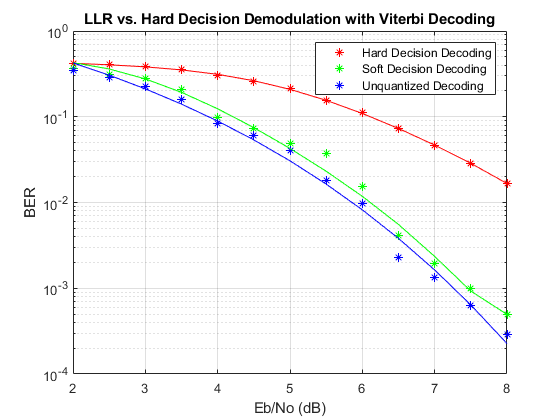
To experiment with this system further, try different modulation types. This system uses a binary mapped modulation scheme for faster error collection but it is well known that Gray mapped signal constellation provides better BER performance. Experiment with various constellation ordering options in the modulator and demodulator blocks. Configure the demodulator block to compute approximate LLR to see the difference in the BER performance compared to hard decision demodulation and LLR. Try out a different range of Eb/No values. Finally, investigate different quantizer boundaries for your modulation scheme and Eb/No values.
Using Dataflow in Simulink
You can configure this example to use data-driven execution by setting the Domain parameter to dataflow for Dataflow Subsystem. With dataflow, blocks inside the domain, execute based on the availability of data as rather than the sample timing in Simulink®. Simulink automatically partitions the system into concurrent threads. This autopartitioning accelerates simulation and increases data throughput. To learn more about dataflow and how to run this example using multiple threads, see Multicore Simulation of Comparing Demodulation Types.
% Cleanup close_system(modelName,0); clear modelName EbNo codeRate nBits Pavg snr noiseVarVector ... ber_HD ber_SD ber_LLR idx noiseVar fitBER_HD fitBER_SD fitBER_LLR;
Selected Bibliography
[1] J. L. Massey, "Coding and Modulation in Digital Communications", Proc. Int. Zurich Seminar on Digital Communications, 1974
[2] J. A. Heller, I. M. Jacobs, "Viterbi Decoding for Satellite and Space Communication", IEEE® Trans. Comm. Tech. vol COM-19, October 1971
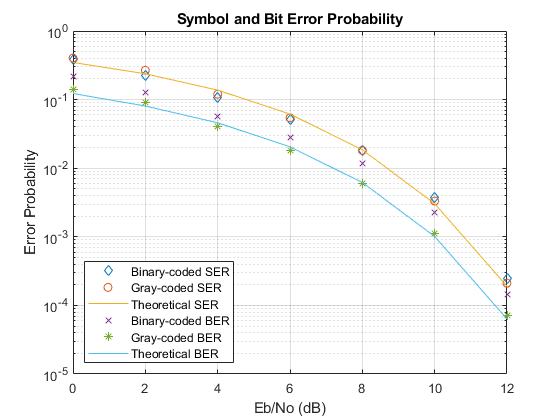
This example uses the doc_gray_code to compute bit error rates (BER) and symbol error rates (SER) for M-PSK modulation. The theoretical error rate performance of M-PSK modulation in AWGN is compared to the error rate performance for Gray-coded symbol mapping and to the error rate performance of binary-coded symbol mapping.
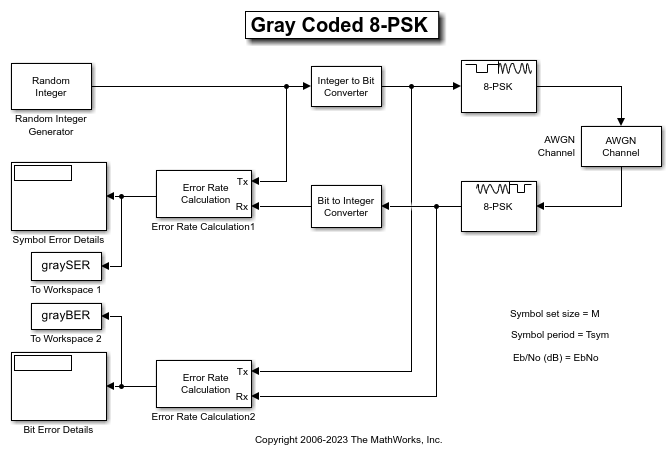
The Random Integer Generator block serves as the source, producing a sequence of integers. The Integer to Bit Converter block converts each integer into a corresponding binary representation. The M-PSK Modulator Baseband block in the doc_gray_code model:
Accepts binary-valued inputs that represent integers in the range [0, (M - 1], where M is the modulation order.
Maps binary representations to constellation points using a Gray-coded ordering.
Produces unit-magnitude complex phasor outputs, with evenly spaced phases in the range [0, (2
 (M - 1) / M)].
(M - 1) / M)].
The AWGN Channel block adds white Gaussian noise to the modulated data. The M-PSK Demodulator Baseband block demodulates the noisy data. The Bit to Integer Converter block converts each binary representation to a corresponding integer. Then two separate Error Rate Calculation blocks calculate the error rates of the demodulated data. The block labeled SER Calculation compares the integer data to compute the symbol error rate statistics and the block labeled BER Calculation compares the bits data to compute the bit error rate statistics. The output of the Error Rate Calculation block is a three-element vector containing the calculated error rate, the number of errors observed, and the amount of data processed.
To reduce simulation run time and ensure that the statistics of the errors remain stable as the Eb/N0 ratio increases, the model is configured to run until 100 errors occur or until 1e8 bits have been transmitted.
The model initializes variables used to configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink).
Produce Error Rate Curves
Compute the theoretical BER for nondifferential 8-PSK in AWGN over a range of Eb/N0 values by using the berawgndoc_gray_code model with Gray-coded symbol mapping over the same range of Eb/N0 values.
Compare Gray coding with binary coding, by modifying the M-PSK Modulator Baseband and M-PSK Demodulator Baseband blocks to set the Constellation ordering parameter to Binary instead of Gray. Simulate the doc_gray_code model with binary-coded symbol mapping over the same range of Eb/N0 values.
Plot the results by using the semilogy function. The Gray-coded system achieves better error rate performance than the binary-coded system. Further, the Gray-coded error rate aligns with the theoretical error rate statistics.
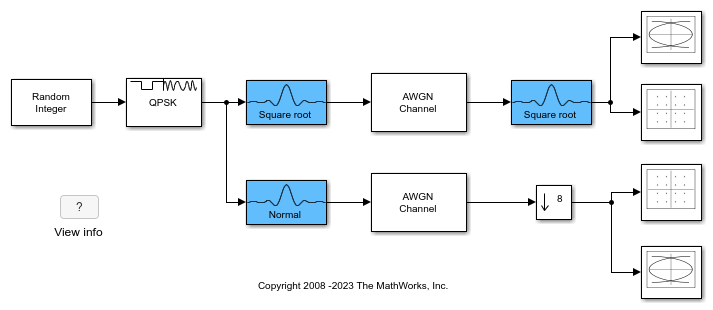
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are designed for raised cosine (RC) filtering. Each block can apply a square-root raised cosine (RRC) filter or a raised cosine filter to a signal. You can vary the roll-off factor and span of the filter.
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are tailored for use at the transmitter and receiver, respectively. The transmit filter upsamples (interpolates) the output signal. The receive filter expects its input signal to be upsampled and downsamples (decimates) the output signal, based on the configured settings of the block.
The raised cosine transmit and receive filter blocks each introduce a propagation delay, as described in Group Delay.
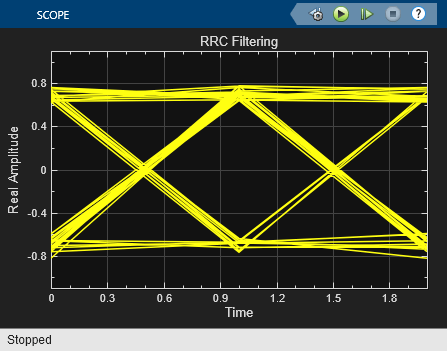
The doc_rrcfiltercompare.slx model shows how to split the filtering equally between the transmitter and the receiver by using a pair of square root raised cosine filters. The use of a matched pair of square root raised cosine filters is equivalent to a single normal raised cosine filter. The filters share the same span and use the same number samples per symbol but the two filter blocks on the upper path have a square root shape and the single filter block on the lower path has the normal shape.
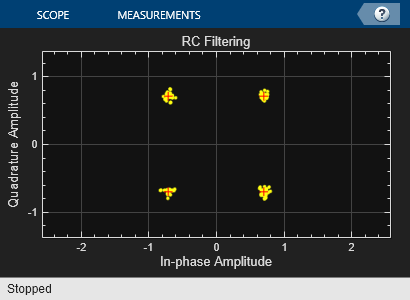
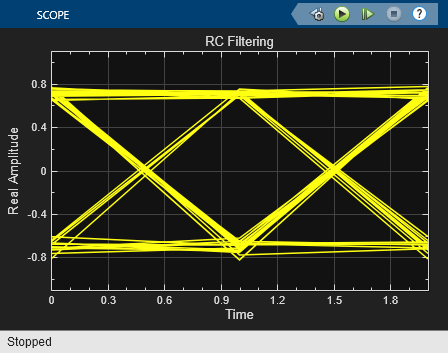
Run the model and observe the eye and constellation diagrams. The performance is nearly identical for the two methods. Note that the limited impulse response of practical square root raised cosine filters causes a slight difference between the response of two cascaded square root raised cosine filters and the response of one raised cosine filter.

Limitations
To use this block in a For Each Subsystem (Simulink) you must set
Random number sourcetoGlobal Streamand the model toNormalorAcceleratorsimulation mode. This ensures that each run will generate independent noise samples.
Ports
Input
Input data signal, specified as an
NS-by-1 vector or an
NS-by-NC
matrix. NS represents the number of samples
in the input signal. NC represents the
number of channels, as determined by the number of columns in the input signal matrix.
Both NS and
NC can be equal to 1.
The block adds frames of length-NS Gaussian noise to each of the NC channels, using a distinct random distribution per channel.
This port is unnamed on the block until the Var port is added.
Data Types: double | single
Complex Number Support: Yes
Variance of additive white Gaussian noise, specified as a positive scalar or a 1-by-NC vector. NC represents the number of channels, as determined by the number of columns in the input signal matrix. For more information, see Specifying the Variance Directly or Indirectly.
Dependencies
To enable this port, set Mode to
Variance and Noise variance
source to Input port.
Data Types: double
Output
Output data signal for the AWGN channel, returned as a vector or matrix. The datatype and dimensions of Out match those of the input signal, In. This port is unnamed on the block.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Variance mode, specified as Signal to noise ratio
(Eb/No), Signal to noise ratio (Es/No),
Signal to noise ratio (SNR), or
Variance. For more information, see Relationship Among Eb/No, Es/No, and SNR Modes and
Specifying the Variance Directly or Indirectly.
Ratio of signal power to noise power in decibels, specified as a scalar or vector.
Tunable: Yes
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (SNR).
Ratio of information bit energy per symbol to noise power spectral density in decibels, specified as a scalar or vector. The information bit energy is the magnitude without channel coding.
Tunable: Yes
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No).
Ratio of information symbol energy per symbol to noise power spectral density in decibels, specified as a scalar or vector. The information symbol energy is the magnitude without channel coding.
Tunable: Yes
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Es/No).
Number of bits in each input symbol, specified as a scalar or vector.
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No).
Mean square power of the input in watts, specified as a scalar or vector.
Tunable: Yes
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No), Signal to
noise ratio (Es/No), or Signal to noise ratio
(SNR).
Select this parameter to specify symbol duration in seconds.
When you select this parameter, set the Symbol period (s) parameter to specify the symbol period in seconds.
When this parameter is not selected, set the Samples per symbol parameter to specify the samples per symbol in samples.
The block determines the sample time and appropriate noise to add at model run time.
For more information, see Relationship Among Eb/No, Es/No, and SNR Modes.
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No) or Signal to
noise ratio (Es/No).
Samples per symbol in samples, specified as a positive integer scalar or vector.
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No) or Signal to
noise ratio (Es/No), and do not select Specify symbol
duration in seconds.
Symbol period in seconds, specified as a positive scalar or vector. When you use this parameter, the block determines the sample time and appropriate noise to add at model run time.
Dependencies
To enable this parameter, set Mode to
Signal to noise ratio (Eb/No) or Signal to
noise ratio (Es/No), and select Specify symbol
duration in seconds.
Noise variance source, specified as a Parameter or
Input port. For more information, see Specifying the Variance Directly or Indirectly.
Tunable: Yes
Dependencies
To enable this parameter, set Mode to
Variance.
Variance of the white Gaussian noise, specified as a scalar or vector. For more information, see Specifying the Variance Directly or Indirectly.
Tunable: Yes
Dependencies
To enable this port, set Mode to
Variance and Noise variance
source to Parameter.
Randomization
Noise generator initial seed for the mt19937ar algorithm, specified as a nonnegative integer.
Tunable: Yes
Dependencies
To enable this parameter, set Random number
source to mt19937ar with seed.
Type of simulation to run, specified as Code generation or
Interpreted execution.
Code generation— Simulate the model by using generated C code. The first time you run a simulation, Simulink generates C code for the block. The model reuses the C code for subsequent simulations unless the model changes. This option requires additional startup time, but the speed of the subsequent simulations is faster than with theInterpreted executionoption.Interpreted execution— Simulate the model by using the MATLAB® interpreter. This option shortens startup time, but the speed of subsequent simulations is slower than with theCode generationoption. In this mode, you can debug the source code of the block.
For more information, see Interpreted Execution vs. Code Generation (Simulink).
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Tips
When running Monte Carlo simulations in code gen or rapid acceleration. Set Random number
source to mt19937ar with seed and make sure that all
blocks have different Initial seed
values when running simulations in parallel using the parsim (Simulink) function, such as for Monte Carlo simulation runs.
Otherwise, the different workers may generate the same random numbers (leading to misleading results) for these model configurations:
If the model is in rapid accelerator mode.
If this block has Simulate using set to
Code generationand Random number source set toGlobal stream.
For more information, see Choosing a Simulation Mode (Simulink).
Algorithms
For uncoded complex input signals, the AWGN Channel block relates Eb/N0, Es/N0, and SNR according to these equations:
Es/N0 = (Tsym/Tsamp) × SNR
Es/N0 = Eb/N0 + 10log10(k) in dB
Es represents the signal energy in joules.
Eb represents the bit energy in joules.
N0 represents the noise power spectral density in watts/Hz.
Tsym/Tsamp equals the value of the Samples per symbol parameter.
Tsym is the symbol period of the signal, in seconds.
Tsamp represents the inherited sample time of the block, in seconds.
k represents the number of information bits per input symbol, Number of bits per symbol.
For real signal inputs, the AWGN Channel block relates Es/N0 and SNR according to this equation:
Es/N0 = 0.5 (Tsym/Tsamp) × SNR
Note
All values of power assume a nominal impedance of 1 ohm.
The equation for the real case differs from the corresponding equation for the complex case by a factor of 2. Specifically, the object uses a noise power spectral density of N0/2 watts/Hz for real input signals, versus N0 watts/Hz for complex signals.
For more information, see AWGN Channel Noise Level.
To directly specify the variance of the noise generated by AWGN Channel, specify the
Mode as
Variance. When you set Noise variance
source to:
Parameter— Specify the variance as a positive scalar or vector by using the Noise variance parameter.Input port— Specify the variance as a positive scalar or vector by using the Var block input. The variance input sampling rate must equal that of the input signal.
When you specify variance as a:
Scalar, all signal channels are uncorrelated but share the same variance.
Vector whose length is the number of channels in the input signal, each element represents the variance of the corresponding signal channel.
Note
For complex-valued input signals the block adds complex zero-mean Gaussian noise with the calculated or specified variance. The variance for each quadrature component of the complex noise is half of the calculated or specified value.
To specify the variance indirectly, that is, to have the block calculate the variance, specify the Mode as:
Signal to noise ratio (Eb/No), where the block calculates the variance from these quantities that you specify in the dialog box:Eb/No (dB), the ratio of bit energy to noise power spectral density
Input signal power, referenced to 1 ohm (watts), the actual power of the symbols at the input of the block
Signal to noise ratio (Es/No), where the block calculates the variance from these quantities that you specify in the dialog box:Es/No (dB), the ratio of signal energy to noise power spectral density
Input signal power, referenced to 1 ohm (watts), the actual power of the symbols at the input of the block
Signal to noise ratio (SNR), where the block calculates the variance from these quantities that you specify in the dialog box:SNR (dB), the ratio of signal power to noise power
Input signal power, referenced to 1 ohm (watts), the actual power of the samples at the input of the block
Changing the symbol period in the AWGN Channel block affects the variance of the noise added per sample, which also causes a change in the final error rate.
Tip
Select the symbol period equal to the symbol period of the model. The value depends on what constitutes a symbol and what the oversampling applied to it is. For example, a symbol could have 3 bits and be oversampled by 4. For more information, see AWGN Channel Noise Level.
References
[1] Proakis, John G. Digital Communications. 4th Ed. McGraw-Hill, 2001.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006aIn R2025a, this block adds the Specify symbol duration in seconds parameter. When you select Specify symbol duration in seconds, you specify the Symbol period (s) parameter value. The block determines the sample time and appropriate noise to add at model run time. For more information, see Specifying the Variance Directly or Indirectly.
In R2023b, use Upgrade Advisor (Simulink) to update instances of the AWGN Channel block in your pre-R2023a models. In addition to the updates for R2023a, these AWGN Channel block updates occur for this configuration:
If the Mode parameter setting is
Signal to noise ratio (Eb/No)orSignal to noise ratio (Es/No)and Symbol period (s) together with the block sample time results in a noninteger samples per symbol, Mode gets set toSignal to noise ratio (SNR)in the upgraded block.The SNR (db) parameter gets set to the appropriate SNR setting.
In R2023a, if the combination of the Symbol period (s) parameter value and the block sample time resulted in a noninteger samples per symbol, using Upgrade Advisor (Simulink) to update the AWGN Channel block generates noise with incorrect variance values.
If you have already updated your block in R2023a:
Select the AWGN Channel block in your model.
Run
set_param(gcb,'LegacyMode','on')at the command line to revert the update.Rerun Upgrade Advisor.
This support enables you to vary the length of input signal each time the block executes in your simulation.
The AWGN Channel block updates the random number generator (RNG) source
permitting selection of Global stream or mt19937ar with
seed.
The new RNG provides better random number statistics. For simulations created before R2023a, the block defaults to legacy mode with prior RNG (Ziggurat method - V5 RANDN algorithm). In this mode, the block uses the Random Source block to generate noise. Random numbers are generated using the Ziggurat method (V5 RANDN algorithm). The block reuses the same initial seeds every time you rerun the simulation, so that this block outputs the same signal each time you run a simulation. To improve statistics, it is recommended that you run Update Model on pre-R2023a simulations that use the AWGN Channel block.
Code generation is enabled by default. For more information, see Simulate using.
See Also
Blocks
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)