小车倒立摆的控制

此示例使用:

打开脚本

此示例使用 systune 来控制小车倒立摆。

摆/小车组件

小车/摆组件如图 1 所示，并使用 Simscape™ Multibody™ 在 Simulink® 中进行建模。

图 1：小车倒立摆

图 2：Simscape Multibody 模型

通过对小车施加可变力 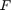$F$ 来控制此系统。在将小车移动到新位置时，或者在摆受到向前的推力（冲激扰动 $dF$）时，控制器需要保持摆处于直立状态。

控制结构

对于倒立摆而言，直立位置是一个不稳定的平衡状态。被控对象的这种不稳定性使得控制任务更具挑战性。对于此示例，使用以下双环控制结构：

open_system('rct_pendulum.slx')
set_param('rct_pendulum','SimMechanicsOpenEditorOnUpdate','off');

内环使用一个二阶状态空间控制器，用于使摆稳定在其直立位置（$\theta$ 控制），而外环使用比例导数 (PD) 控制器来控制小车的位置。之所以使用 PD 控制器而不是 PID 控制器，是因为被控对象本身已提供了一定的积分作用。

设计需求

使用 TuningGoal 需求来指定期望的闭环行为。指定响应时间为 3 秒，来跟踪小车位置 $x$ 的设定点变化。

% Tracking of x command
req1 = TuningGoal.Tracking('xref','x',3);

为了充分抑制摆顶端的冲激扰动 $dF$，使用以下形式的 LQR 惩罚项：

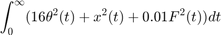
$$ \int_0^\infty (16 \theta^2(t) + x^2(t) + 0.01 F^2(t)) dt $$

该项强调较小的角度偏差 $\theta$，并限制控制力度 $F$。

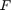% Rejection of impulse disturbance dF
Qxu = diag([16 1 0.01]);
req2 = TuningGoal.LQG('dF',{'Theta','x','F'},1,Qxu);

为了保证鲁棒性，要求在被控对象的输入端至少有 6 dB 的增益裕度和 40 度的相位裕度。

% Stability margins
req3 = TuningGoal.Margins('F',6,40);

最后，对闭环极点的阻尼和固有频率进行约束，以防止出现剧烈或欠阻尼的瞬态响应。

% Pole locations
MinDamping = 0.5;
MaxFrequency = 45;
req4 = TuningGoal.Poles(0,MinDamping,MaxFrequency);

控制系统调节

对于 PD 控制器和状态空间控制器的初始值（分别为 1 和 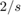$2/s$），闭环系统是不稳定的。您可以使用 systune 来联合调节这两个控制器。使用 slTuner 接口来指定可调模块，并将被控对象输入 F 注册为用于衡量稳定裕度的分析点。

ST0 = slTuner('rct_pendulum',{'Position Controller','Angle Controller'});
addPoint(ST0,'F');

接下来，使用 systune 根据上面指定的性能要求来调节 PD 控制器和状态空间控制器。在满足稳定裕度和极点位置约束（硬要求）的前提下，优化跟踪性能和抗扰性能（软要求）。

rng(0)
Options = systuneOptions('RandomStart',5);
[ST, fSoft] = systune(ST0,[req1,req2],[req3,req4],Options);

Final: Soft = 1.36, Hard = 0.99945, Iterations = 272
Final: Soft = 1.44, Hard = 0.99917, Iterations = 138
Final: Soft = 1.44, Hard = 0.99749, Iterations = 364
Final: Soft = 1.26, Hard = 0.99967, Iterations = 314
Final: Soft = 1.44, Hard = 0.99877, Iterations = 241
Final: Soft = 1.4, Hard = 0.99866, Iterations = 298

最佳设计在满足硬要求 (Hard<1) 的同时，能使软要求的值接近 1。这意味着调节后的控制系统在满足稳定裕度和极点位置约束的同时，几乎达到了目标跟踪和抗扰性能。

验证

使用 viewGoal 进一步分析最佳设计如何满足各项要求。

figure('Position',[100   100   575   660])
viewGoal([req1,req3,req4],ST)

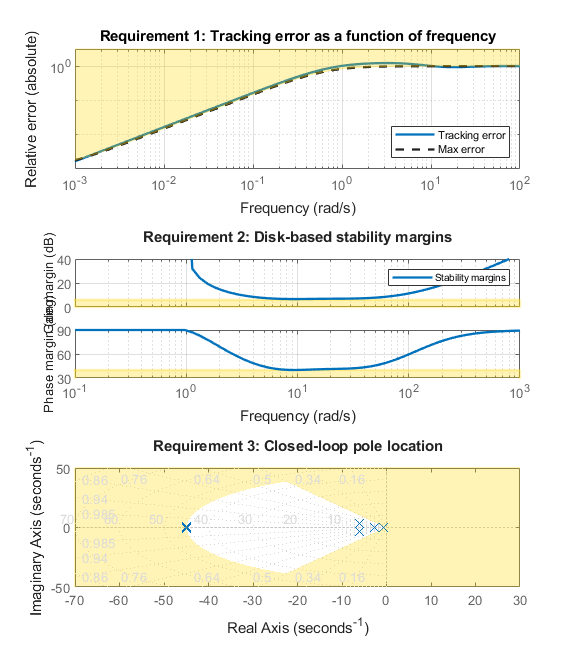
这些绘图证实，前两项要求几乎得到满足，而后两项要求则得到严格执行。接下来，绘制对位置阶跃变化以及小车所受力冲激的响应。

T = getIOTransfer(ST,{'xref','dF'},{'x','Theta'});
figure('Position',[100   100   650   420]);
subplot(121), step(T(:,1),10)
title('Tracking of set point change in position')
subplot(122), impulse(T(:,2),10)
title('Rejection of impulse disturbance')

响应曲线平滑，且达到预期的稳定时间。检查控制器的调节值。

C1 = getBlockValue(ST,'Position Controller')

C1 =
 
               s    
  Kp + Kd * --------
             Tf*s+1 

  with Kp = 5.89, Kd = 1.93, Tf = 0.051
 
Name: Position_Controller
Continuous-time PDF controller in parallel form.

C2 = zpk(getBlockValue(ST,'Angle Controller'))

C2 =
 
  -1614.3 (s+12.9) (s+4.304)
  --------------------------
     (s+135.2) (s-14.28)
 
Name: Angle_Controller
Continuous-time zero/pole/gain model.

请注意，角度控制器有一个不稳定极点，它与被控对象的不稳定极点配对，从而使倒立摆稳定。为了验证这一点，获取被控对象输入端处的开环传递函数，并绘制根轨迹图。

L = getLoopTransfer(ST,'F',-1);
figure
rlocus(L)
set(gca,'XLim',[-25 20],'YLim',[-20 20])

为了完成验证，将调节值上传到 Simulink 中，并对小车/摆组件的非线性响应进行仿真。下面是结果仿真的视频。

writeBlockValue(ST)

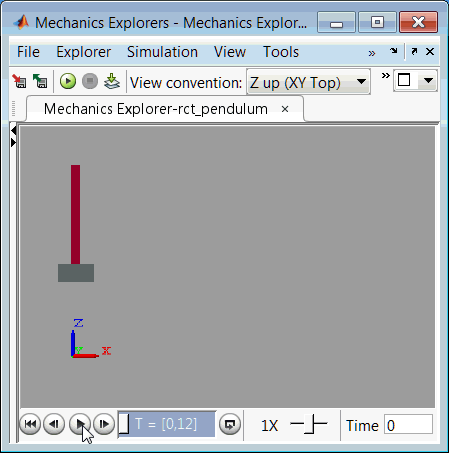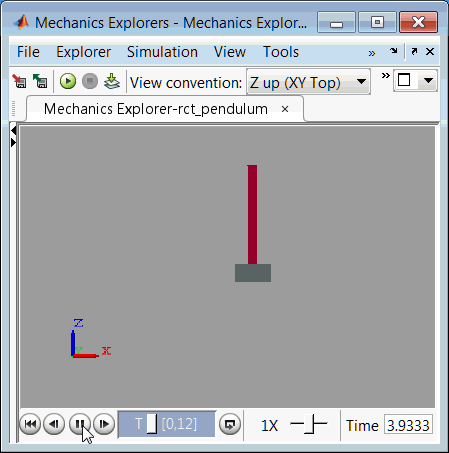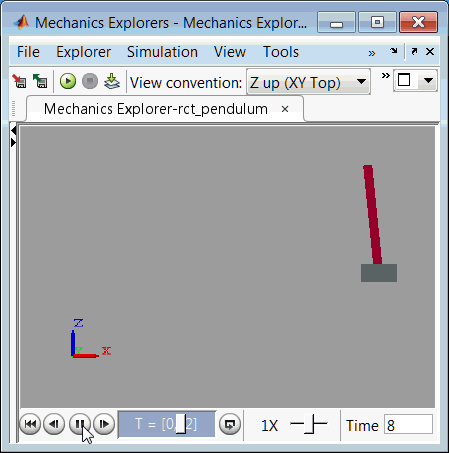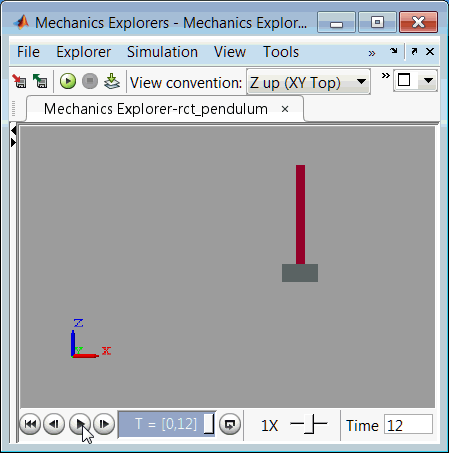
图 3：使用已调节控制器的小车/摆组件仿真。

仿真完成后关闭模型。

set_param('rct_pendulum','SimMechanicsOpenEditorOnUpdate','on');
close_system('rct_pendulum',0);

另请参阅

(Simulink Control Design) | (Simulink Control Design)

主题