SIN 数据集

第一个基准数据集是简单的函数逼近问题。一个 1-5-1 网络（在隐含层具有 tansig 传递函数，在输出层具有线性传递函数）用于逼近正弦波的单个周期。下表摘要显示了使用九种不同训练算法训练网络的结果。表中的每个条目表示 30 次不同尝试，每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.002。对于此问题，最快的算法是莱文贝格-马夸特算法。平均来说，它的速度是仅次于它的算法的四倍以上。这是 LM 算法最适合的问题类型 - 函数逼近问题，其中网络的权重数少于 100 个，逼近必须非常准确。

各种算法的性能可能会受到逼近准确度要求的影响。下图显示了这一点，它是几种代表性算法的均方误差对执行时间（30 次尝试取平均值）的图。在此处，您可以看到，随着时间的推移，LM 算法的误差比所示的其他算法减少得更快。

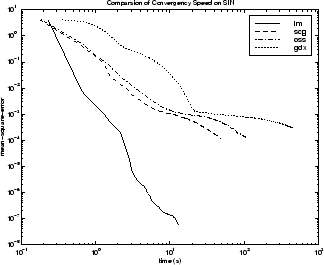
下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。此处您可以看到，随着误差目标的减小，LM 算法提供的改进变得更加显著。一些算法随着误差目标的降低而表现得更好（LM 和 BFG），而其他算法随着误差目标的降低而表现得更差（OSS 和 GDX）。

PARITY 数据集

第二个基准测试问题是简单的模式识别问题 - 检测一个 3 位数的奇偶性。如果输入模式中的 1 的数量是奇数，则网络应输出 1；否则，它应输出 -1。用于求解此问题的网络是一个 3-10-10-1 网络，它的每个层中都有 tansig 神经元。下表摘要显示了用九种不同算法训练该网络的结果。表中的每个条目表示 30 次不同尝试，每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.001。对于此问题，最快的算法是弹性反向传播算法，尽管共轭梯度算法（特别是量化共轭梯度算法）几乎同样快。请注意，LM 算法在此问题上表现不佳。一般来说，LM 算法在模式识别问题上的表现不如在函数逼近问题上的表现好。LM 算法是为近似线性的最小二乘问题设计的。由于模式识别问题中的输出神经元通常是饱和的，因此您不会在线性区域中操作。

与函数逼近问题一样，各种算法的性能会受到网络所需准确度的影响。下图显示了这一点，它是一些典型算法的均方误差对执行时间的图。LM 算法在某一点后会快速收敛，但收敛的时间晚于其他算法。

下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。您可以再次看到，随着误差目标的减小，一些算法的性能下降（OSS 和 BFG）。

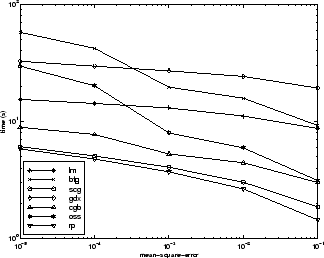
ENGINE 数据集

第三个基准问题是一个现实的函数逼近（或非线性回归）问题。这些数据是从某发动机运行中获得的。网络的输入是发动机转速和供油水平，网络的输出是扭矩和排放水平。用于求解此问题的网络是一个 2-30-2 网络，它的隐藏层中有 tansig 神经元，输出层中有线性神经元。下表摘要显示了用九种不同算法训练该网络的结果。表中的每个条目表示 30 次不同尝试（由于时间限制，RP 和 GDX 各有 10 次尝试），每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.005。对于此问题，最快的算法是 LM 算法，其次是 BFGS 拟牛顿算法和共轭梯度算法。尽管这是函数逼近问题，但 LM 算法并不像在 SIN 数据集上那样优势明显。在本例中，网络中权重和偏置的数量远远大于在 SIN 问题中使用的权重和偏置的数量（152 对 16），并且 LM 算法的优势随着网络参数个数的增加而减弱。

以下是一些典型算法的均方误差对执行时间的图。随着时间的推移，LM 算法的性能相对于其他算法逐渐改善。

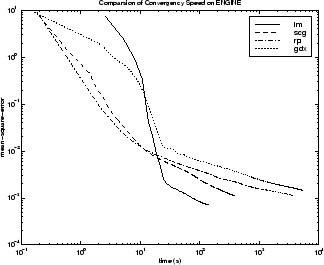
下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。您可以再次看到，随着误差目标的减小，一些算法的性能下降（GDX 和 RP），而 LM 算法却不断改善。

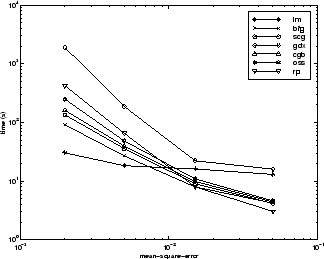
CANCER 数据集

第四个基准问题是一个现实的模式识别（或非线性判别分析）问题。网络的目标是根据显微镜检查收集的细胞特征将肿瘤分为良性或恶性。输入属性包括团块厚度、细胞大小和细胞形状的均匀性、边粘附量和裸核的频率。这些数据来自麦迪逊威斯康星大学医院的威廉·沃尔伯格博士。用于求解此问题的网络是一个 9-5-5-2 网络，它的所有层中都有 tansig 神经元。下表摘要显示了用九种不同算法训练该网络的结果。表中的每个条目表示 30 次不同尝试，每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.012。一些算法的若干次运行未收敛，因此只使用每个算法的前 75% 的运行次数来获得统计数据。

共轭梯度算法和弹性反向传播都能快速收敛，而 LM 算法的收敛也相当快。与在 PARITY 数据集上一样，LM 算法在模式识别问题上的表现不如在函数逼近问题上的表现好。

以下是一些典型算法的均方误差对执行时间的图。对于此问题，性能的差异没有在以前的问题中那样表现明显。

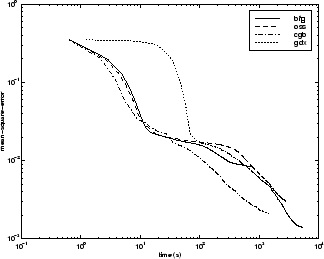
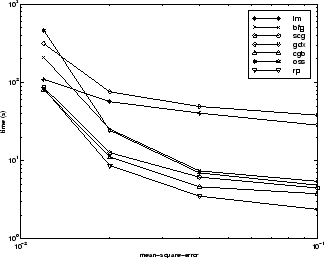
下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。您可以再次看到，随着误差目标的减小，一些算法的性能下降（OSS 和 BFG），而 LM 算法却不断改善。在任何问题上，随着误差目标的降低，LM 算法的性能通常都会相对于其他算法逐渐改善。

CHOLESTEROL 数据集

第五个基准问题是一个现实的函数逼近（或非线性回归）问题。网络的目标是根据对 21 种频谱分量的测量来预测胆固醇水平（ldl、hdl 和 vldl）。数据来自俄克拉荷马州立大学化学系的 Neil Purdie 博士 [PuLu92]。用于求解此问题的网络是一个 21-15-3 网络，它的隐藏层中有 tansig 神经元，输出层中有线性神经元。下表摘要显示了用九种不同算法训练该网络的结果。表中的每个条目表示 20 次不同尝试（RP 和 GDX 各有 10 次尝试），每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.027。

量化共轭梯度算法在此问题上性能最佳，尽管所有共轭梯度算法的性能都很好。LM 算法在此函数逼近问题上的表现不如在另外两个问题上的表现好。这是因为网络中权重和偏置的数量再次增大（378 对 152 对 16）。随着参数个数的增加，LM 算法所需的计算量呈几何增长。

以下是一些典型算法的均方误差对执行时间的图。对于此问题，您可以看到，相对于其他算法，LM 算法能够将均方误差降低到更低的水平。SCG 和 RP 算法具有最快的初始收敛。

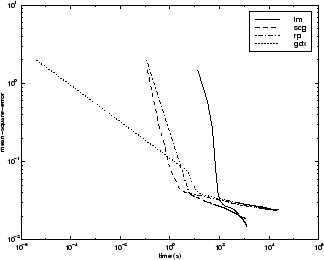
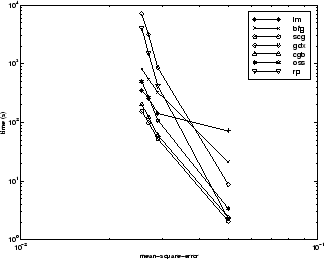
下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。您可以看到，随着误差目标的降低，相对于其他算法，LM 和 BFG 算法的性能不断改善。

DIABETES 数据集

第六个基准问题是一个模式识别问题。网络的目标是根据个人数据（年龄、怀孕次数）和医学检查结果（如血压、体重指数、葡萄糖耐量试验结果等）来诊断个人是否患有糖尿病。这些数据来自加州大学欧文分校的机器学习数据库。用于求解此问题的网络是一个 8-15-15-2 网络，它的所有层中都有 tansig 神经元。下表摘要显示了用九种不同算法训练该网络的结果。表中的每个条目表示 10 次不同尝试，每次尝试使用不同的随机初始权重。在每种情况下，网络会持续训练，直到平方误差小于 0.05。

共轭梯度算法和弹性反向传播都能快速收敛。此问题的结果与所考虑的其他模式识别问题是一致的。RP 算法在所有模式识别问题上都效果良好。这是合理的，因为该算法旨在克服用 sigmoid 函数进行训练所带来的困难，当远离中心点执行运算时，sigmoid 函数具有非常小的斜率。对于模式识别问题，您要在输出层中使用 sigmoid 传递函数，并且要网络在 sigmoid 函数的尾部运行。

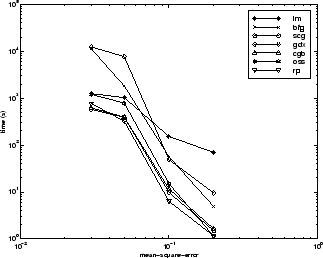
以下是一些典型算法的均方误差对执行时间的图。与其他问题一样，您可以看到 SCG 和 RP 具有快速的初始收敛，而 LM 算法能够提供较小的最终误差。

下图进一步说明各算法之间的关系，它是收敛所需的时间对均方误差收敛目标的图。在本例中，您可以看到随着误差目标的降低，BFG 算法的性能下降，而 LM 算法的性能不断改善。RP 算法表现最好，除了在最小的误差目标上 SCG 表现更好。

总结

从上述试验中可以推断出几个算法特征。一般情况下，在函数逼近问题上，对于包含多达几百个权重的网络，莱文贝格-马夸特算法具有最快的收敛。如果需要非常准确的训练，这种优势尤其明显。在许多情况下，trainlm 能够获得比任何其他被测算法更低的均方误差。然而，随着网络中权重数量的增加，trainlm 的优势会减小。此外，trainlm 在模式识别问题上的表现相对较差。trainlm 的存储要求高于被测的其他算法。

trainrp 函数是在模式识别问题上最快的算法。然而，它在函数逼近问题上表现不佳。随着误差目标的降低，其性能也会下降。与考虑的其他算法相比，该算法的内存要求相对较小。

共轭梯度算法，特别是 trainscg，似乎在各种各样的问题上都表现良好，特别是对于具有大量权重个数的网络。SCG 算法在函数逼近问题上几乎与 LM 算法一样快（对于大型网络更快），在模式识别问题上几乎与 trainrp 一样快。当误差减小时，其性能不会像 trainrp 性能下降得那样快。共轭梯度算法具有相对适中的内存要求。

trainbfg 的表现与 trainlm 相似。它不需要像 trainlm 那样多的存储空间，但所需的计算量确实会随着网络规模的增大而呈几何增长，因为每次迭代都必须计算等效逆矩阵。

可变学习率算法 traingdx 通常比其他方法慢得多，其存储要求与 trainrp 大致相同，但它仍可用于求解某些问题。在某些情况下，收敛速度越慢越好。例如，当使用早停法时，如果使用收敛过快的算法，可能会产生不一致的结果。您可能会过冲在验证集上误差最小化的点。