设计层循环神经网络
下一个要介绍的动态网络是层循环网络 (LRN)。此网络的早期简化版本是由埃尔曼 [Elma90] 引入的。在 LRN 中,除了最后一层外,每层网络都有一个带有单一延迟的反馈环路。最初的埃尔曼网络只有两个层,对隐藏层使用 tansig 传递函数,对输出层使用 purelin 传递函数。使用近似反向传播算法对原始埃尔曼网络进行训练。layrecnet 命令将埃尔曼网络泛化为具有任意数量的层,并且在每层中具有任意传递函数。工具箱使用 多层浅层神经网络与反向传播训练 中讨论的基于梯度的算法的精确版本来训练 LRN。下图显示一个包含两个层的 LRN。

LRN 配置用于许多已讨论的滤波和建模应用中。为了显示其操作,此示例使用 pH 数据集。以下是加载数据以及创建和训练网络的代码:
[p,t] = ph_dataset;
lrn_net = layrecnet(1,8);
lrn_net.trainFcn = 'trainbr';
lrn_net.trainParam.show = 5;
lrn_net.trainParam.epochs = 50;
lrn_net = train(lrn_net,p,t);
训练后,您可以使用以下代码绘制响应:
y = lrn_net(p); plot(cell2mat(y)) hold on plot(cell2mat(t)) legend(["Predicted" "Target"]) hold off
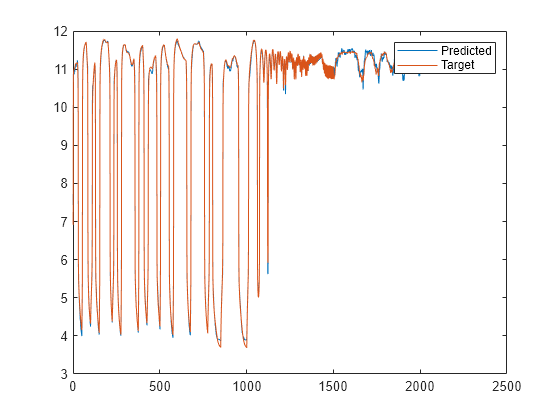
绘图显示网络能够检测溶液的 pH 值。
每次训练神经网络时,由于初始权重和偏置值不同,并且将数据划分为训练集、验证集和测试集的方式也不同,可能会产生不同的解。因此,针对同一问题训练的不同神经网络对同一输入可能给出不同输出。为确保找到准确度良好的神经网络,需要多次重新训练。
如果需要更高的准确度,可以采用几种其他方法来改进初始解。有关详细信息,请参阅提高浅层神经网络泛化能力,避免过拟合。