Improve Shallow Neural Network Generalization and Avoid Overfitting

Tip

To learn how to set up parameters for a deep learning network, see trainingOptions.

One of the problems that occur during neural network training is called overfitting. The error on the training set is driven to a very small value, but when new data is presented to the network the error is large. The network has memorized the training examples, but it has not learned to generalize to new situations.

The following figure shows the response of a 1-20-1 neural network that has been trained to approximate a noisy sine function. The underlying sine function is shown by the dotted line, the noisy measurements are given by the + symbols, and the neural network response is given by the solid line. Clearly this network has overfitted the data and will not generalize well.

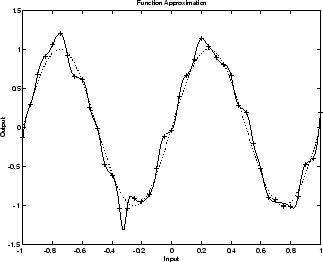
Output versus input for a neural network trained to approximate a noisy sine function. The solid line goes through nearly all of the plus symbols representing the noisy data.

One method for improving network generalization is to use a network that is just large enough to provide an adequate fit. The larger network you use, the more complex the functions the network can create. If you use a small enough network, it will not have enough power to overfit the data.

Unfortunately, it is difficult to know beforehand how large a network should be for a specific application. There are two other methods for improving generalization that are implemented in Deep Learning Toolbox™ software: regularization and early stopping. The next sections describe these two techniques and the routines to implement them.

Note that if the number of parameters in the network is much smaller than the total number of points in the training set, then there is little or no chance of overfitting. If you can easily collect more data and increase the size of the training set, then there is no need to worry about the following techniques to prevent overfitting. The rest of this section only applies to those situations in which you want to make the most of a limited supply of data.

Retraining Neural Networks

Typically each backpropagation training session starts with different initial weights and biases, and different divisions of data into training, validation, and test sets. These different conditions can lead to very different solutions for the same problem.

It is a good idea to train several networks to ensure that a network with good generalization is found.

Here a dataset is loaded and divided into two parts: 90% for designing networks and 10% for testing them all.

[x, t] = bodyfat_dataset;
Q = size(x, 2);
Q1 = floor(Q * 0.90);
Q2 = Q - Q1;
ind = randperm(Q);
ind1 = ind(1:Q1);
ind2 = ind(Q1 + (1:Q2));
x1 = x(:, ind1);
t1 = t(:, ind1);
x2 = x(:, ind2);
t2 = t(:, ind2);

Next a network architecture is chosen and trained ten times on the first part of the dataset, with each network’s mean square error on the second part of the dataset.

net = feedforwardnet(10);
numNN = 10;
NN = cell(1, numNN);
perfs = zeros(1, numNN);
for i = 1:numNN
  fprintf('Training %d/%d\n', i, numNN);
  NN{i} = train(net, x1, t1);
  y2 = NN{i}(x2);
  perfs(i) = mse(net, t2, y2);
end

Each network will be trained starting from different initial weights and biases, and with a different division of the first dataset into training, validation, and test sets. Note that the test sets are a good measure of generalization for each respective network, but not for all the networks, because data that is a test set for one network will likely be used for training or validation by other neural networks. This is why the original dataset was divided into two parts, to ensure that a completely independent test set is preserved.

The neural network with the lowest performance is the one that generalized best to the second part of the dataset.

Multiple Neural Networks

Another simple way to improve generalization, especially when caused by noisy data or a small dataset, is to train multiple neural networks and average their outputs.

For instance, here 10 neural networks are trained on a small problem and their mean squared errors compared to the means squared error of their average.

First, the dataset is loaded and divided into a design and test set.

[x, t] = bodyfat_dataset;
Q = size(x, 2);
Q1 = floor(Q * 0.90);
Q2 = Q - Q1;
ind = randperm(Q);
ind1 = ind(1:Q1);
ind2 = ind(Q1 + (1:Q2));
x1 = x(:, ind1);
t1 = t(:, ind1);
x2 = x(:, ind2);
t2 = t(:, ind2);

Then, ten neural networks are trained.

net = feedforwardnet(10);
numNN = 10;
nets = cell(1, numNN);
for i = 1:numNN
  fprintf('Training %d/%d\n', i, numNN)
  nets{i} = train(net, x1, t1);
end

Next, each network is tested on the second dataset with both individual performances and the performance for the average output calculated.

perfs = zeros(1, numNN);
y2Total = 0;
for i = 1:numNN
  neti = nets{i};
  y2 = neti(x2);
  perfs(i) = mse(neti, t2, y2);
  y2Total = y2Total + y2;
end
perfs
y2AverageOutput = y2Total / numNN;
perfAveragedOutputs = mse(nets{1}, t2, y2AverageOutput)

The mean squared error for the average output is likely to be lower than most of the individual performances, perhaps not all. It is likely to generalize better to additional new data.

For some very difficult problems, a hundred networks can be trained and the average of their outputs taken for any input. This is especially helpful for a small, noisy dataset in conjunction with the Bayesian Regularization training function trainbr, described below.

Early Stopping

The default method for improving generalization is called early stopping. This technique is automatically provided for all of the supervised network creation functions, including the backpropagation network creation functions such as feedforwardnet.

In this technique the available data is divided into three subsets. The first subset is the training set, which is used for computing the gradient and updating the network weights and biases. The second subset is the validation set. The error on the validation set is monitored during the training process. The validation error normally decreases during the initial phase of training, as does the training set error. However, when the network begins to overfit the data, the error on the validation set typically begins to rise. When the validation error increases for a specified number of iterations (net.trainParam.max_fail), the training is stopped, and the weights and biases at the minimum of the validation error are returned.

The test set error is not used during training, but it is used to compare different models. It is also useful to plot the test set error during the training process. If the error in the test set reaches a minimum at a significantly different iteration number than the validation set error, this might indicate a poor division of the data set.

There are four functions provided for dividing data into training, validation and test sets. They are dividerand (the default), divideblock, divideint, and divideind. You can access or change the division function for your network with this property:

net.divideFcn

Each of these functions takes parameters that customize its behavior. These values are stored and can be changed with the following network property:

net.divideParam

Index Data Division (divideind)

Create a simple test problem. For the full data set, generate a noisy sine wave with 201 input points ranging from −1 to 1 at steps of 0.01:

p = [-1:0.01:1];
t = sin(2*pi*p)+0.1*randn(size(p));

Divide the data by index so that successive samples are assigned to the training set, validation set, and test set successively:

trainInd = 1:3:201
valInd = 2:3:201;
testInd = 3:3:201;
[trainP,valP,testP] = divideind(p,trainInd,valInd,testInd);
[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

Random Data Division (dividerand)

You can divide the input data randomly so that 60% of the samples are assigned to the training set, 20% to the validation set, and 20% to the test set, as follows:

[trainP,valP,testP,trainInd,valInd,testInd] = dividerand(p);

This function not only divides the input data, but also returns indices so that you can divide the target data accordingly using divideind:

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

Block Data Division (divideblock)

You can also divide the input data randomly such that the first 60% of the samples are assigned to the training set, the next 20% to the validation set, and the last 20% to the test set, as follows:

[trainP,valP,testP,trainInd,valInd,testInd] = divideblock(p);

Divide the target data accordingly using divideind:

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

Interleaved Data Division (divideint)

Another way to divide the input data is to cycle samples between the training set, validation set, and test set according to percentages. You can interleave 60% of the samples to the training set, 20% to the validation set and 20% to the test set as follows:

[trainP,valP,testP,trainInd,valInd,testInd] = divideint(p);

Divide the target data accordingly using divideind.

[trainT,valT,testT] = divideind(t,trainInd,valInd,testInd);

Regularization

Another method for improving generalization is called regularization. This involves modifying the performance function, which is normally chosen to be the sum of squares of the network errors on the training set. The next section explains how the performance function can be modified, and the following section describes a routine that automatically sets the optimal performance function to achieve the best generalization.

Modified Performance Function

The typical performance function used for training feedforward neural networks is the mean sum of squares of the network errors.

$F = m s e = \frac{1}{N} \sum_{i = 1}^{N} {(e_{i})}^{2} = \frac{1}{N} \sum_{i = 1}^{N} {(t_{i} - α_{i})}^{2}$

It is possible to improve generalization if you modify the performance function by adding a term that consists of the mean of the sum of squares of the network weights and biases $m s e r e g = γ * m s w + (1 - γ) * m s e$ , where $γ$ is the performance ratio, and

$m s w = \frac{1}{n} \sum_{j = 1}^{n} w_{j}^{2}$

Using this performance function causes the network to have smaller weights and biases, and this forces the network response to be smoother and less likely to overfit.

The following code reinitializes the previous network and retrains it using the BFGS algorithm with the regularized performance function. Here the performance ratio is set to 0.5, which gives equal weight to the mean square errors and the mean square weights.

[x,t] = simplefit_dataset;
net = feedforwardnet(10,'trainbfg');
net.divideFcn = '';
net.trainParam.epochs = 300;
net.trainParam.goal = 1e-5;
net.performParam.regularization = 0.5;
net = train(net,x,t);

The problem with regularization is that it is difficult to determine the optimum value for the performance ratio parameter. If you make this parameter too large, you might get overfitting. If the ratio is too small, the network does not adequately fit the training data. The next section describes a routine that automatically sets the regularization parameters.

Automated Regularization (trainbr)

It is desirable to determine the optimal regularization parameters in an automated fashion. One approach to this process is the Bayesian framework of David MacKay [MacK92]. In this framework, the weights and biases of the network are assumed to be random variables with specified distributions. The regularization parameters are related to the unknown variances associated with these distributions. You can then estimate these parameters using statistical techniques.

A detailed discussion of Bayesian regularization is beyond the scope of this user guide. A detailed discussion of the use of Bayesian regularization, in combination with Levenberg-Marquardt training, can be found in [FoHa97].

Bayesian regularization has been implemented in the function trainbr. The following code shows how you can train a 1-20-1 network using this function to approximate the noisy sine wave shown in the figure in Improve Shallow Neural Network Generalization and Avoid Overfitting. (Data division is cancelled by setting net.divideFcn so that the effects of trainbr are isolated from early stopping.)

x = -1:0.05:1;
t = sin(2*pi*x) + 0.1*randn(size(x));
net = feedforwardnet(20,'trainbr');
net = train(net,x,t);

One feature of this algorithm is that it provides a measure of how many network parameters (weights and biases) are being effectively used by the network. In this case, the final trained network uses approximately 12 parameters (indicated by #Par in the printout) out of the 61 total weights and biases in the 1-20-1 network. This effective number of parameters should remain approximately the same, no matter how large the number of parameters in the network becomes. (This assumes that the network has been trained for a sufficient number of iterations to ensure convergence.)

The trainbr algorithm generally works best when the network inputs and targets are scaled so that they fall approximately in the range [−1,1]. That is the case for the test problem here. If your inputs and targets do not fall in this range, you can use the function mapminmax or mapstd to perform the scaling, as described in Choose Neural Network Input-Output Processing Functions. Networks created with feedforwardnet include mapminmax as an input and output processing function by default.

The following figure shows the response of the trained network. In contrast to the previous figure, in which a 1-20-1 network overfits the data, here you see that the network response is very close to the underlying sine function (dotted line), and, therefore, the network will generalize well to new inputs. You could have tried an even larger network, but the network response would never overfit the data. This eliminates the guesswork required in determining the optimum network size.

When using trainbr, it is important to let the algorithm run until the effective number of parameters has converged. The training might stop with the message "Maximum MU reached." This is typical, and is a good indication that the algorithm has truly converged. You can also tell that the algorithm has converged if the sum squared error (SSE) and sum squared weights (SSW) are relatively constant over several iterations. When this occurs you might want to click the stop button in the training window.

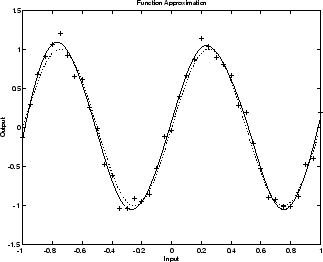
Output versus input for a neural network trained to approximate a noisy sine function. The solid line closely matches the dotted line representing the underlying sine function.

Summary and Discussion of Early Stopping and Regularization

Early stopping and regularization can ensure network generalization when you apply them properly.

For early stopping, you must be careful not to use an algorithm that converges too rapidly. If you are using a fast algorithm (like trainlm), set the training parameters so that the convergence is relatively slow. For example, set mu to a relatively large value, such as 1, and set mu_dec and mu_inc to values close to 1, such as 0.8 and 1.5, respectively. The training functions trainscg and trainbr usually work well with early stopping.

With early stopping, the choice of the validation set is also important. The validation set should be representative of all points in the training set.

When you use Bayesian regularization, it is important to train the network until it reaches convergence. The sum-squared error, the sum-squared weights, and the effective number of parameters should reach constant values when the network has converged.

With both early stopping and regularization, it is a good idea to train the network starting from several different initial conditions. It is possible for either method to fail in certain circumstances. By testing several different initial conditions, you can verify robust network performance.

When the data set is small and you are training function approximation networks, Bayesian regularization provides better generalization performance than early stopping. This is because Bayesian regularization does not require that a validation data set be separate from the training data set; it uses all the data.

To provide some insight into the performance of the algorithms, both early stopping and Bayesian regularization were tested on several benchmark data sets, which are listed in the following table.

Data Set Title	Number of Points	Network	Description
BALL	67	2-10-1	Dual-sensor calibration for a ball position measurement
SINE (5% N)	41	1-15-1	Single-cycle sine wave with Gaussian noise at 5% level
SINE (2% N)	41	1-15-1	Single-cycle sine wave with Gaussian noise at 2% level
ENGINE (ALL)	1199	2-30-2	Engine sensor—full data set
ENGINE (1/4)	300	2-30-2	Engine sensor—1/4 of data set
CHOLEST (ALL)	264	5-15-3	Cholesterol measurement—full data set
CHOLEST (1/2)	132	5-15-3	Cholesterol measurement—1/2 data set

These data sets are of various sizes, with different numbers of inputs and targets. With two of the data sets the networks were trained once using all the data and then retrained using only a fraction of the data. This illustrates how the advantage of Bayesian regularization becomes more noticeable when the data sets are smaller. All the data sets are obtained from physical systems except for the SINE data sets. These two were artificially created by adding various levels of noise to a single cycle of a sine wave. The performance of the algorithms on these two data sets illustrates the effect of noise.

The following table summarizes the performance of early stopping (ES) and Bayesian regularization (BR) on the seven test sets. (The trainscg algorithm was used for the early stopping tests. Other algorithms provide similar performance.)

Mean Squared Test Set Error

Method	Ball	Engine (All)	Engine (1/4)	Choles (All)	Choles (1/2)	Sine (5% N)	Sine (2% N)
ES	1.2e-1	1.3e-2	1.9e-2	1.2e-1	1.4e-1	1.7e-1	1.3e-1
BR	1.3e-3	2.6e-3	4.7e-3	1.2e-1	9.3e-2	3.0e-2	6.3e-3
ES/BR	92	5	4	1	1.5	5.7	21

You can see that Bayesian regularization performs better than early stopping in most cases. The performance improvement is most noticeable when the data set is small, or if there is little noise in the data set. The BALL data set, for example, was obtained from sensors that had very little noise.

Although the generalization performance of Bayesian regularization is often better than early stopping, this is not always the case. In addition, the form of Bayesian regularization implemented in the toolbox does not perform as well on pattern recognition problems as it does on function approximation problems. This is because the approximation to the Hessian that is used in the Levenberg-Marquardt algorithm is not as accurate when the network output is saturated, as would be the case in pattern recognition problems. Another disadvantage of the Bayesian regularization method is that it generally takes longer to converge than early stopping.

Posttraining Analysis (regression)

The performance of a trained network can be measured to some extent by the errors on the training, validation, and test sets, but it is often useful to investigate the network response in more detail. One option is to perform a regression analysis between the network response and the corresponding targets. The routine regression is designed to perform this analysis.

The following commands illustrate how to perform a regression analysis on a network trained.

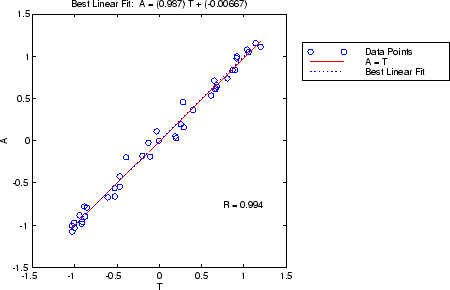
x = [-1:.05:1];
t = sin(2*pi*x)+0.1*randn(size(x));
net = feedforwardnet(10);
net = train(net,x,t);
y = net(x);
[r,m,b] = regression(t,y)

r =
    0.9935
m =
    0.9874
b =
   -0.0067

The network output and the corresponding targets are passed to regression. It returns three parameters. The first two, m and b, correspond to the slope and the y-intercept of the best linear regression relating targets to network outputs. If there were a perfect fit (outputs exactly equal to targets), the slope would be 1, and the y-intercept would be 0. In this example, you can see that the numbers are very close. The third variable returned by regression is the correlation coefficient (R-value) between the outputs and targets. It is a measure of how well the variation in the output is explained by the targets. If this number is equal to 1, then there is perfect correlation between targets and outputs. In the example, the number is very close to 1, which indicates a good fit.

The following figure illustrates the graphical output provided by regression. The network outputs are plotted versus the targets as open circles. The best linear fit is indicated by a dashed line. The perfect fit (output equal to targets) is indicated by the solid line. In this example, it is difficult to distinguish the best linear fit line from the perfect fit line because the fit is so good.

Outputs versus targets with lines showing the best linear fit and the perfect fit.