针对回归训练卷积神经网络
此示例说明如何训练卷积神经网络来预测手写数字的旋转角度。
回归任务涉及预测连续数值而不是离散类标签。此示例为回归构造卷积神经网络架构,训练网络,并使用经过训练的网络来预测旋转手写数字的角度。
下图说明通过回归神经网络的图像数据流。
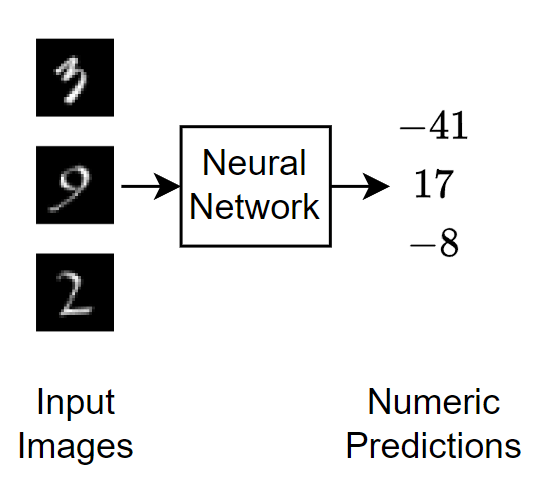
加载数据
数据集包含手写数字的合成图像以及每个图像的旋转角度(以度为单位)。
分别从 MAT 文件 DigitsDataTrain.mat 和 DigitsDataTest.mat 中加载训练数据和测试数据。变量 anglesTrain 和 anglesTest 是以度为单位的旋转角度。训练数据集和测试数据集各包含 5000 个图像。
load DigitsDataTrain load DigitsDataTest
显示一些训练图像。
numObservations = size(XTrain,4); idx = randperm(numObservations,49); I = imtile(XTrain(:,:,:,idx)); figure imshow(I);
使用 trainingPartitions 函数将 XTrain 和 anglesTrain 分区为训练分区和验证分区,此函数作为支持文件包含在此示例中。要访问此函数,请以实时脚本形式打开此示例。留出 15% 的训练数据用于验证。
[idxTrain,idxValidation] = trainingPartitions(numObservations,[0.85 0.15]); XValidation = XTrain(:,:,:,idxValidation); anglesValidation = anglesTrain(idxValidation); XTrain = XTrain(:,:,:,idxTrain); anglesTrain = anglesTrain(idxTrain);
检查数据归一化
在训练神经网络时,最好确保数据在网络的所有阶段均归一化。对于使用梯度下降的网络训练,归一化有助于训练的稳定和加速。如果您的数据缩放不当,则损失可能会变为 NaN,并且网络参数在训练过程中可能发生偏离。归一化数据的常用方法包括重新缩放数据,使其范围变为 [0,1],或使其均值为 0 且标准差为 1。您可以归一化以下数据:
输入数据。在将预测变量输入到网络之前对其进行归一化。在此示例中,输入图像已归一化到范围 [0,1]。
层输出。您可以使用批量归一化层来归一化每个卷积层和全连接层的输出。
响应。如果使用批量归一化层来归一化网络末尾的层输出,则网络的预测值在训练开始时就被归一化。如果响应的比例与这些预测值完全不同,则网络训练可能无法收敛。如果您的响应缩放不当,则尝试对其进行归一化,并查看网络训练是否有所改善。如果在训练之前将响应归一化,则必须变换经过训练网络的预测值,以获得原始响应的预测值。
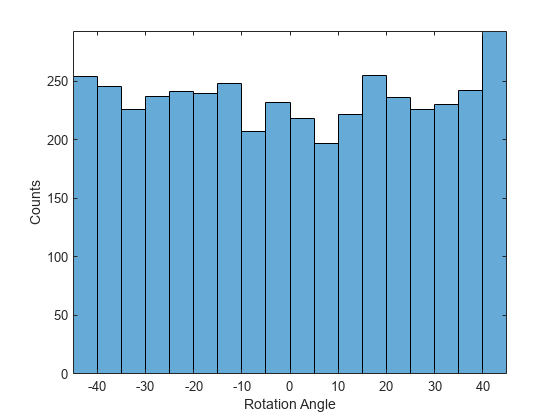
绘制响应的分布。响应(以度为单位的旋转角度)大致均匀地分布在 -45 和 45 之间,效果很好,无需归一化。在分类问题中,输出是类概率,始终需要归一化。
figure histogram(anglesTrain) axis tight ylabel("Counts") xlabel("Rotation Angle")
通常,数据不必完全归一化。但是,如果在此示例中训练网络来预测 100*anglesTrain 或 anglesTrain+500 而不是 anglesTrain,则损失将变为 NaN,并且网络参数在训练开始时会发生偏离。即使预测 的网络与预测 的网络之间的唯一差异是对最终全连接层的权重和偏置的简单重新缩放,也会出现这些结果。
如果输入或响应的分布非常不均匀或偏斜,您还可以在训练网络之前对数据执行非线性变换(例如,取其对数)。
定义神经网络架构
定义神经网络架构。
对于图像输入,指定一个图像输入层。
指定四个 convolution-batchnorm-ReLU 模块,并增加滤波器数量。
在每个模块之间指定一个具有池化区域的平均池化层,步幅大小为 2。
在网络末尾,包含一个全连接层,其输出大小与响应数量匹配。
numResponses = 1;
layers = [
imageInputLayer([28 28 1])
convolution2dLayer(3,8,Padding="same")
batchNormalizationLayer
reluLayer
averagePooling2dLayer(2,Stride=2)
convolution2dLayer(3,16,Padding="same")
batchNormalizationLayer
reluLayer
averagePooling2dLayer(2,Stride=2)
convolution2dLayer(3,32,Padding="same")
batchNormalizationLayer
reluLayer
convolution2dLayer(3,32,Padding="same")
batchNormalizationLayer
reluLayer
fullyConnectedLayer(numResponses)];指定训练选项
指定训练选项。在选项中进行选择需要经验分析。要通过运行试验探索不同训练选项配置,您可以使用Experiment Manager。
将初始学习率设置为 0.001,并在 20 轮训练后降低学习率。
通过指定验证数据和验证频率,监控训练过程中的网络准确度。软件基于训练数据训练网络,并在训练过程中按固定时间间隔计算基于验证数据的准确度。验证数据不用于更新网络权重。
在图中显示训练进度并监控均方根误差。
禁用详尽输出。
miniBatchSize = 128; validationFrequency = floor(numel(anglesTrain)/miniBatchSize); options = trainingOptions("sgdm", ... MiniBatchSize=miniBatchSize, ... InitialLearnRate=1e-3, ... LearnRateSchedule="piecewise", ... LearnRateDropFactor=0.1, ... LearnRateDropPeriod=20, ... Shuffle="every-epoch", ... ValidationData={XValidation,anglesValidation}, ... ValidationFrequency=validationFrequency, ... Plots="training-progress", ... Metrics="rmse", ... Verbose=false);
训练神经网络
使用 trainnet 函数训练神经网络。对于回归,请使用均方误差损失。默认情况下,trainnet 函数使用 GPU(如果有)。使用 GPU 需要 Parallel Computing Toolbox™ 许可证和受支持的 GPU 设备。有关受支持设备的信息,请参阅GPU 计算要求 (Parallel Computing Toolbox)。否则,该函数使用 CPU。要指定执行环境,请使用 ExecutionEnvironment 训练选项。
net = trainnet(XTrain,anglesTrain,layers,"mse",options);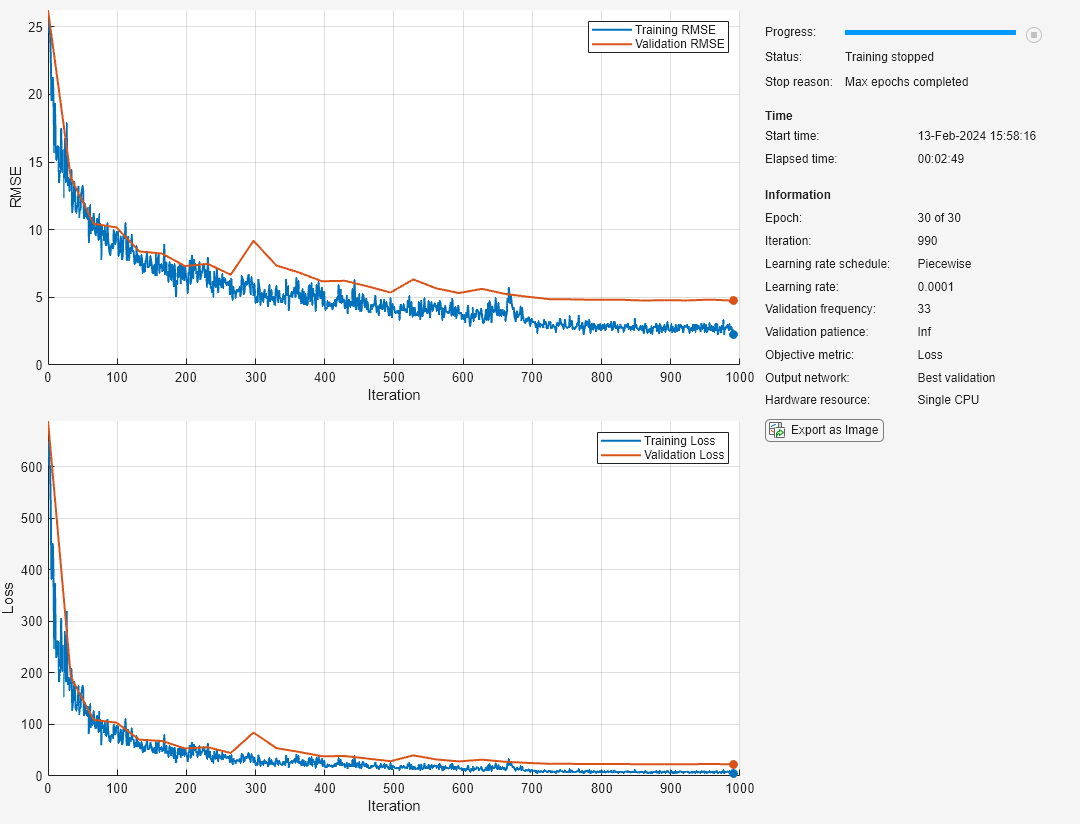
测试网络
使用 testnet 函数测试神经网络。对于回归,请计算均方根误差 (RMSE)。默认情况下,testnet 函数使用 GPU(如果有)。要手动选择执行环境,请使用 testnet 函数的 ExecutionEnvironment 参量。
rmse = testnet(net,XTest,anglesTest,"rmse")rmse = 4.9274
通过使用测试数据进行预测并将预测结果与目标进行比较,可视化绘图的准确度。使用 minibatchpredict 函数进行预测。默认情况下,minibatchpredict 函数使用 GPU(如果有)。
YTest = minibatchpredict(net,XTest);
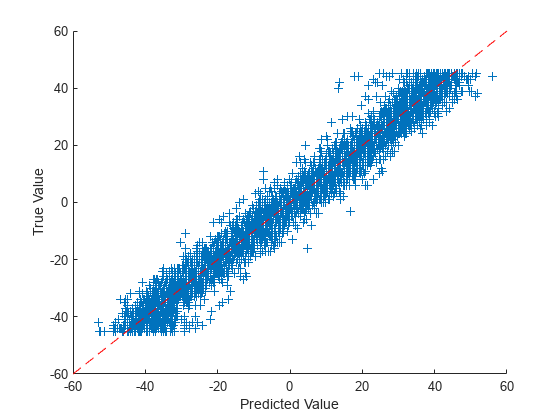
绘制预测值对目标的图。
figure scatter(YTest,anglesTest,"+") xlabel("Prediction") ylabel("Target") hold on plot([-60 60], [-60 60],"r--")
使用新数据进行预测
使用神经网络对第一个测试图像进行预测。要使用单个图像进行预测,请使用 predict 函数。要使用 GPU,请先将数据转换为 gpuArray。
X = XTest(:,:,:,1); if canUseGPU X = gpuArray(X); end Y = predict(net,X)
Y = single
34.7356
figure
imshow(X)
title("Angle: " + gather(Y))
另请参阅
trainnet | trainingOptions | dlnetwork