Update Batch Normalization Statistics Using Model Function

This example shows how to update the network state in a network defined as a function.

A batch normalization operation normalizes each input channel across a mini-batch. To speed up training of convolutional neural networks and reduce the sensitivity to network initialization, use batch normalization operations between convolutions and nonlinearities, such as ReLU layers.

During training, batch normalization operations first normalize the activations of each channel by subtracting the mini-batch mean and dividing by the mini-batch standard deviation. Then, the operation shifts the input by a learnable offset β and scales it by a learnable scale factor γ.

When you use a trained network to make predictions on new data, the batch normalization operations use the trained data set mean and variance instead of the mini-batch mean and variance to normalize the activations.

To compute the data set statistics, you must keep track of the mini-batch statistics by using a continually updating state.

If you use batch normalization operations in a model function, then you must define the behavior for both training and prediction. For example, you can specify a Boolean option doTraining to control whether the model uses mini-batch statistics for training or data set statistics for prediction.

This example piece of code from a model function shows how to apply a batch normalization operation and update only the data set statistics during training.

if doTraining
    [Y,trainedMean,trainedVariance] = batchnorm(Y,offset,scale,trainedMean,trainedVariance);
    
    % Update state
    state.batchnorm1.TrainedMean = trainedMean;
    state.batchnorm1.TrainedVariance = trainedVariance;
else
    Y = batchnorm(Y,offset,scale,trainedMean,trainedVariance);
end

Load Training Data

The digitTrain4DArrayData function loads the images, their digit labels, and their angles of rotation from the vertical. Create an arrayDatastore object for the images, labels, and the angles, and then use the combine function to make a single datastore that contains all of the training data. Extract the class names and number of nondiscrete responses.

[XTrain,TTrain,anglesTrain] = digitTrain4DArrayData;

dsXTrain = arrayDatastore(XTrain,IterationDimension=4);
dsTTrain = arrayDatastore(TTrain);
dsAnglesTrain = arrayDatastore(anglesTrain);

dsTrain = combine(dsXTrain,dsTTrain,dsAnglesTrain);

classNames = categories(TTrain);
numClasses = numel(classNames);
numResponses = size(anglesTrain,2);
numObservations = numel(TTrain);

View some images from the training data.

idx = randperm(numObservations,64);
I = imtile(XTrain(:,:,:,idx));
figure
imshow(I)

Define Deep Learning Model

Define the following network that predicts both labels and angles of rotation.

A convolution-batchnorm-ReLU block with 16 5-by-5 filters.
A branch of two convolution-batchnorm blocks each with 32 3-by-3 filters with a ReLU operation between
A skip connection with a convolution-batchnorm block with 32 1-by-1 convolutions.
Combine both branches using addition followed by a ReLU operation
For the regression output, a branch with a fully connected operation of size 1 (the number of responses).
For classification output, a branch with a fully connected operation of size 10 (the number of classes) and a softmax operation.

Define and Initialize Model Parameters and State

Define the parameters for each of the operations and include them in a struct. Use the format parameters.OperationName.ParameterName where parameters is the struct, OperationName is the name of the operation (for example "conv1") and ParameterName is the name of the parameter (for example, "Weights").

Create a struct parameters containing the model parameters. Initialize the learnable layer weights and biases using the initializeGlorot and initializeZeros example functions, respectively. Initialize the batch normalization offset and scale parameters with the initializeZeros and initializeOnes example functions, respectively.

To perform training and inference using batch normalization layers, you must also manage the network state. Before prediction, you must specify the dataset mean and variance derived from the training data. Create a struct state containing the state parameters. The batch normalization statistics must not be dlarray objects. Initialize the batch normalization trained mean and trained variance states using the zeros and ones functions, respectively.

The initialization example functions are attached to this example as supporting files.

Initialize the parameters for the first convolutional layer.

filterSize = [5 5];
numChannels = 1;
numFilters = 16;

sz = [filterSize numChannels numFilters];
numOut = prod(filterSize) * numFilters;
numIn = prod(filterSize) * numFilters;

parameters.conv1.Weights = initializeGlorot(sz,numOut,numIn);
parameters.conv1.Bias = initializeZeros([numFilters 1]);

Initialize the parameters and state for the first batch normalization layer.

parameters.batchnorm1.Offset = initializeZeros([numFilters 1]);
parameters.batchnorm1.Scale = initializeOnes([numFilters 1]);
state.batchnorm1.TrainedMean = initializeZeros([numFilters 1]);
state.batchnorm1.TrainedVariance = initializeOnes([numFilters 1]);

Initialize the parameters for the second convolutional layer.

filterSize = [3 3];
numChannels = 16;
numFilters = 32;

sz = [filterSize numChannels numFilters];
numOut = prod(filterSize) * numFilters;
numIn = prod(filterSize) * numFilters;

parameters.conv2.Weights = initializeGlorot(sz,numOut,numIn);
parameters.conv2.Bias = initializeZeros([numFilters 1]);

Initialize the parameters and state for the second batch normalization layer.

parameters.batchnorm2.Offset = initializeZeros([numFilters 1]);
parameters.batchnorm2.Scale = initializeOnes([numFilters 1]);
state.batchnorm2.TrainedMean = initializeZeros([numFilters 1]);
state.batchnorm2.TrainedVariance = initializeOnes([numFilters 1]);

Initialize the parameters for the third convolutional layer.

filterSize = [3 3];
numChannels = 32;
numFilters = 32;

sz = [filterSize numChannels numFilters];
numOut = prod(filterSize) * numFilters;
numIn = prod(filterSize) * numFilters;

parameters.conv3.Weights = initializeGlorot(sz,numOut,numIn);
parameters.conv3.Bias = initializeZeros([numFilters 1]);

Initialize the parameters and state for the third batch normalization layer.

parameters.batchnorm3.Offset = initializeZeros([numFilters 1]);
parameters.batchnorm3.Scale = initializeOnes([numFilters 1]);
state.batchnorm3.TrainedMean = initializeZeros([numFilters 1]);
state.batchnorm3.TrainedVariance = initializeOnes([numFilters 1]);

Initialize the parameters for the convolutional layer in the skip connection.

filterSize = [1 1];
numChannels = 16;
numFilters = 32;

sz = [filterSize numChannels numFilters];
numOut = prod(filterSize) * numFilters;
numIn = prod(filterSize) * numFilters;

parameters.convSkip.Weights = initializeGlorot(sz,numOut,numIn);
parameters.convSkip.Bias = initializeZeros([numFilters 1]);

Initialize the parameters and state for the batch normalization layer in the skip connection.

parameters.batchnormSkip.Offset = initializeZeros([numFilters 1]);
parameters.batchnormSkip.Scale = initializeOnes([numFilters 1]);
state.batchnormSkip.TrainedMean = initializeZeros([numFilters 1]);
state.batchnormSkip.TrainedVariance = initializeOnes([numFilters 1]);

Initialize the parameters for the fully connected layer corresponding to the classification output.

sz = [numClasses 6272];
numOut = numClasses;
numIn = 6272;
parameters.fc1.Weights = initializeGlorot(sz,numOut,numIn);
parameters.fc1.Bias = initializeZeros([numClasses 1]);

Initialize the parameters for the fully connected layer corresponding to the regression output.

sz = [numResponses 6272];
numOut = numResponses;
numIn = 6272;
parameters.fc2.Weights = initializeGlorot(sz,numOut,numIn);
parameters.fc2.Bias = initializeZeros([numResponses 1]);

View the struct of the state.

state

state = struct with fields:
       batchnorm1: [1×1 struct]
       batchnorm2: [1×1 struct]
       batchnorm3: [1×1 struct]
    batchnormSkip: [1×1 struct]

View the state parameters for the batchnorm1 operation.

state.batchnorm1

ans = struct with fields:
        TrainedMean: [16×1 dlarray]
    TrainedVariance: [16×1 dlarray]

Define Model Function

Create the function model, listed at the end of the example, which computes the outputs of the deep learning model described earlier.

The function model takes as input the model parameters parameters, input data, the flag doTraining, which specifies whether the model returns outputs for training or prediction, and the network state state. The network outputs the predictions for the labels, the predictions for the angles, and the updated network state.

Define Model Loss Function

Create the function modelLoss, listed at the end of the example, which takes as input a mini-batch of input data with corresponding targets T1 and T2 containing the labels and angles, respectively, and returns the loss, the gradients of the loss with respect to the learnable parameters, and the updated network state.

Specify Training Options

Specify the training options.

numEpochs = 20;
miniBatchSize = 128;

Train Model

Train the model using a custom training loop. Use minibatchqueue to process and manage the mini-batches of images. For each mini-batch:

Use the custom mini-batch preprocessing function preprocessMiniBatch (defined at the end of this example) to one-hot encode the class labels.
Format the image data with the dimension labels "SSCB" (spatial, spatial, channel, batch). By default, the minibatchqueue object converts the data to dlarray objects with underlying type single. Do not add a format to the class labels or the angles.
Train on a GPU if one is available. By default, the minibatchqueue object converts each output to a gpuArray if a GPU is available. Using a GPU requires Parallel Computing Toolbox™ and a supported GPU device. For information on supported devices, see GPU Computing Requirements (Parallel Computing Toolbox).

mbq = minibatchqueue(dsTrain,...
    MiniBatchSize=miniBatchSize,...
    MiniBatchFcn=@preprocessMiniBatch,...
    MiniBatchFormat=["SSCB" "" ""]);

For each epoch, shuffle the data and loop over mini-batches of data. At the end of each epoch, display the training progress. For each mini-batch:

Evaluate the model loss and gradients using dlfeval and the modelLoss function.
Update the network parameters using the adamupdate function.

Initialize the parameters for the Adam solver.

trailingAvg = [];
trailingAvgSq = [];

Calculate the total number of iterations for the training progress monitor.

numIterationsPerEpoch = ceil(numObservations / miniBatchSize);
numIterations = numEpochs * numIterationsPerEpoch;

Initialize the TrainingProgressMonitor object. Because the timer starts when you create the monitor object, make sure that you create the object close to the training loop.

monitor = trainingProgressMonitor(Metrics="Loss",Info=["Epoch","Iteration"],XLabel="Iteration");

Train the model.

iteration = 0;
epoch = 0;
start = tic;

% Loop over epochs.
while epoch < numEpochs && ~monitor.Stop
    epoch = epoch + 1;

    % Shuffle data.
    shuffle(mbq)

    % Loop over mini-batches
    while hasdata(mbq) && ~monitor.Stop
        iteration = iteration + 1;

        [X,T1,T2] = next(mbq);

        % Evaluate the model loss, gradients, and state using dlfeval and the
        % modelLoss function.
        [loss,gradients,state] = dlfeval(@modelLoss,parameters,X,T1,T2,state);

        % Update the network parameters using the Adam optimizer.
        [parameters,trailingAvg,trailingAvgSq] = adamupdate(parameters,gradients, ...
            trailingAvg,trailingAvgSq,iteration);

        recordMetrics(monitor,iteration,Loss=loss);
        updateInfo(monitor,Epoch=epoch,Iteration=iteration);
        monitor.Progress = 100*iteration/numIterations;
    end
end

Test Model

Test the classification accuracy of the model by comparing the predictions on a test set with the true labels and angles. Manage the test data set using a minibatchqueue object with the same setting as the training data.

[XTest,T1Test,anglesTest] = digitTest4DArrayData;

dsXTest = arrayDatastore(XTest,IterationDimension=4);
dsTTest = arrayDatastore(T1Test);
dsAnglesTest = arrayDatastore(anglesTest);

dsTest = combine(dsXTest,dsTTest,dsAnglesTest);

mbqTest = minibatchqueue(dsTest,...
    MiniBatchSize=miniBatchSize,...
    MiniBatchFcn=@preprocessMiniBatch,...
    MiniBatchFormat=["SSCB" "" ""]);

To predict the labels and angles of the validation data, use the modelPredictions function, listed at the end of the example. The function returns the predicted classes and angles, as well as comparison with the true values.

[classesPredictions,anglesPredictions,classCorr,angleDiff] = modelPredictions(parameters,state,mbqTest,classNames);

Evaluate the classification accuracy.

accuracy = mean(classCorr)

accuracy = 0.9858

Evaluate the regression accuracy.

angleRMSE = sqrt(mean(angleDiff.^2))

angleRMSE = single
    7.1762

View some of the images with their predictions. Display the predicted angles in red and the correct angles in green.

idx = randperm(size(XTest,4),9);
figure
for i = 1:9
    subplot(3,3,i)
    I = XTest(:,:,:,idx(i));
    imshow(I)
    hold on

    sz = size(I,1);
    offset = sz/2;

    thetaPred = anglesPredictions(idx(i));
    plot(offset*[1-tand(thetaPred) 1+tand(thetaPred)],[sz 0],"r--")

    thetaValidation = anglesTest(idx(i));
    plot(offset*[1-tand(thetaValidation) 1+tand(thetaValidation)],[sz 0],"g--")

    hold off
    label = string(classesPredictions(idx(i)));
    title("Label: " + label)
end

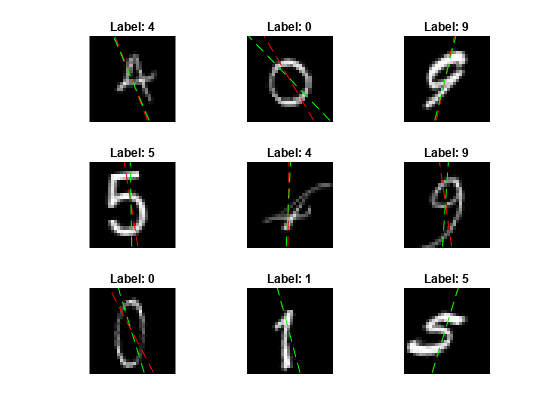
Model Function

The function model takes as input the model parameters parameters, the input data X, the flag doTraining, which specifies whether the model returns the outputs for training or prediction, and the network state state. The function returns the predictions for the labels, the predictions for the angles, and the updated network state.

function [Y1,Y2,state] = model(parameters,X,doTraining,state)

% Convolution
weights = parameters.conv1.Weights;
bias = parameters.conv1.Bias;
Y = dlconv(X,weights,bias,Padding=2);

% Batch normalization, ReLU
offset = parameters.batchnorm1.Offset;
scale = parameters.batchnorm1.Scale;
trainedMean = state.batchnorm1.TrainedMean;
trainedVariance = state.batchnorm1.TrainedVariance;

if doTraining
    [Y,trainedMean,trainedVariance] = batchnorm(Y,offset,scale,trainedMean,trainedVariance);

    % Update state
    state.batchnorm1.TrainedMean = trainedMean;
    state.batchnorm1.TrainedVariance = trainedVariance;
else
    Y = batchnorm(Y,offset,scale,trainedMean,trainedVariance);
end

Y = relu(Y);

% Convolution, batch normalization (skip connection)
weights = parameters.convSkip.Weights;
bias = parameters.convSkip.Bias;
YSkip = dlconv(Y,weights,bias,Stride=2);

offset = parameters.batchnormSkip.Offset;
scale = parameters.batchnormSkip.Scale;
trainedMean = state.batchnormSkip.TrainedMean;
trainedVariance = state.batchnormSkip.TrainedVariance;

if doTraining
    [YSkip,trainedMean,trainedVariance] = batchnorm(YSkip,offset,scale,trainedMean,trainedVariance);

    % Update state
    state.batchnormSkip.TrainedMean = trainedMean;
    state.batchnormSkip.TrainedVariance = trainedVariance;
else
    YSkip = batchnorm(YSkip,offset,scale,trainedMean,trainedVariance);
end

% Convolution
weights = parameters.conv2.Weights;
bias = parameters.conv2.Bias;
Y = dlconv(Y,weights,bias,Padding=1,Stride=2);

% Batch normalization, ReLU
offset = parameters.batchnorm2.Offset;
scale = parameters.batchnorm2.Scale;
trainedMean = state.batchnorm2.TrainedMean;
trainedVariance = state.batchnorm2.TrainedVariance;

if doTraining
    [Y,trainedMean,trainedVariance] = batchnorm(Y,offset,scale,trainedMean,trainedVariance);

    % Update state
    state.batchnorm2.TrainedMean = trainedMean;
    state.batchnorm2.TrainedVariance = trainedVariance;
else
    Y = batchnorm(Y,offset,scale,trainedMean,trainedVariance);
end

Y = relu(Y);

% Convolution
weights = parameters.conv3.Weights;
bias = parameters.conv3.Bias;
Y = dlconv(Y,weights,bias,Padding=1);

% Batch normalization
offset = parameters.batchnorm3.Offset;
scale = parameters.batchnorm3.Scale;
trainedMean = state.batchnorm3.TrainedMean;
trainedVariance = state.batchnorm3.TrainedVariance;

if doTraining
    [Y,trainedMean,trainedVariance] = batchnorm(Y,offset,scale,trainedMean,trainedVariance);

    % Update state
    state.batchnorm3.TrainedMean = trainedMean;
    state.batchnorm3.TrainedVariance = trainedVariance;
else
    Y = batchnorm(Y,offset,scale,trainedMean,trainedVariance);
end

% Addition, ReLU
Y = YSkip + Y;
Y = relu(Y);

% Fully connect, softmax (labels)
weights = parameters.fc1.Weights;
bias = parameters.fc1.Bias;
Y1 = fullyconnect(Y,weights,bias);
Y1 = softmax(Y1);

% Fully connect (angles)
weights = parameters.fc2.Weights;
bias = parameters.fc2.Bias;
Y2 = fullyconnect(Y,weights,bias);

end

Model Loss Function

The modelLoss function takes as input the model parameters, a mini-batch of the input data X with corresponding targets T1 and T2 containing the labels and angles, respectively, and returns the loss, the gradients of the loss with respect to the learnable parameters, and the updated network state.

function [loss,gradients,state] = modelLoss(parameters,X,T1,T2,state)

doTraining = true;
[Y1,Y2,state] = model(parameters,X,doTraining,state);

lossLabels = crossentropy(Y1,T1);
lossAngles = mse(Y2,T2);

loss = lossLabels + 0.1*lossAngles;
gradients = dlgradient(loss,parameters);

end

Model Predictions Function

The modelPredictions function takes the model parameters, the network state, a minibatchqueue of input data mbq, and the network classes, and returns the model predictions by iterating over all data in the minibatchqueue using the model function with the doTraining option set to false. The function returns the predicted classes and angles, as well as comparison with the true values. For the classes, the comparison is a vector of ones and zeros that represents correct and incorrect predictions. For the angles, the comparison is the difference between the predicted angle and the true value.

function [classesPredictions,anglesPredictions,classCorr,angleDiff] = modelPredictions(parameters,state,mbq,classes)

doTraining = false;

classesPredictions = [];
anglesPredictions = [];
classCorr = [];
angleDiff = [];

while hasdata(mbq)
    [X,T1,T2] = next(mbq);

    % Make predictions using the model function.
    [Y1,Y2] = model(parameters,X,doTraining,state);

    % Determine predicted classes.
    Y1PredBatch = onehotdecode(Y1,classes,1);
    classesPredictions = [classesPredictions Y1PredBatch];

    % Dermine predicted angles
    Y2PredBatch = extractdata(Y2);
    anglesPredictions = [anglesPredictions Y2PredBatch];

    % Compare predicted and true classes
    Y1 = onehotdecode(T1,classes,1);
    classCorr = [classCorr Y1PredBatch == Y1];

    % Compare predicted and true angles
    angleDiffBatch = Y2PredBatch - T2;
    angleDiff = [angleDiff extractdata(gather(angleDiffBatch))];

end

end

Mini-Batch Preprocessing Function

The preprocessMiniBatch function preprocesses the data using the following steps:

Extract the image data from the incoming cell array and concatenate into a numeric array. Concatenating the image data over the fourth dimension adds a third dimension to each image, to be used as a singleton channel dimension.
Extract the label and angle data from the incoming cell arrays and concatenate into a categorical array and a numeric array, respectively.
One-hot encode the categorical labels into numeric arrays. Encoding into the first dimension produces an encoded array that matches the shape of the network output.

function [X,T,angle] = preprocessMiniBatch(dataX,dataT,dataAngle)

% Extract image data from cell and concatenate
X = cat(4,dataX{:});

% Extract label data from cell and concatenate
T = cat(2,dataT{:});

% Extract angle data from cell and concatenate
angle = cat(2,dataAngle{:});

% One-hot encode labels
T = onehotencode(T,1);

end