Smooth GPS Waypoints for Ego Localization

This example uses:

This example shows how to smooth an ego trajectory obtained from the Global Positioning System (GPS) and Inertial Measurement Unit (IMU) sensors.

You can use virtual driving scenarios to recreate real-world scenarios from recorded vehicle data. To generate a reliable virtual scenario, you must have accurate trajectory information. You can obtain ego trajectory information from GPS and IMU sensors. However, data from these sensors is often noisy which results in inaccurate waypoints. You can smooth these noisy waypoints to accurately localize the ego vehicle.

In this example, you preprocess the GPS data and smooth noisy ego waypoints using a kinematic motion model and a window-based statistical model.

Load and Preprocess GPS Data

Download the GPS data. The data contains a structure with these fields:

timeStamp — Time at which the data was collected. Units are in microseconds.
velocity — Velocity of the ego vehicle. Units are in meters per second.
yawRate — Yaw rate of the ego vehicle. Units are in degrees.
latitude — Latitude coordinate values of the ego trajectory. Units are in degrees.
longitude — Longitude coordinate values of the ego trajectory. Units are in degrees.
altitude — Altitude values of the ego trajectory. Units are in meters.

sensorData = fullfile(tempdir,"AutomotiveDataset");
if ~isfolder(sensorData)
    mkdir(sensorData)
end
if ~exist("data","var")
    url = "https://ssd.mathworks.com/supportfiles/driving/data/highwayLaneChangeDatase/ins2.mat";
    filePath = fullfile(sensorData,"ins.mat");
    if ~isfile(filePath)
        websave(filePath,url);
    end
    data = load(filePath);
end

Insert the startTime, egoSampleTime and endTime to the sim object.

startTime — Time to start collecting the data. Units are in microseconds.
endTime — Time to stop collecting the data. Units are in microseconds.
egoSampleTime — Time interval between each consecutive data point. Units are in microseconds.

sim.startTime = 1461634424950000;
sim.endTime = 1461634434950000;
sim.egoSampleTime = 0.05;

Compute the start and end timestamp indices, and the number of data points, by using the helperTimestampIndex function.

[~,sim.gps.startstep,sim.gps.endstep] = helperTimestampIndex([data.ins.timeStamp]',sim.startTime,sim.endTime);

Extract the GPS data for the specified timestamp range.

dataSelected.ins = data.ins(sim.gps.startstep:sim.gps.endstep);
gps = table([dataSelected.ins.timeStamp]',[dataSelected.ins.latitude]',[dataSelected.ins.longitude]',[dataSelected.ins.altitude]',VariableNames=["Timestamp","Latitude","Longitude","Altitude"]);

gps is an M-by-4 table containing latitude, longitude, and altitude values for each timestamp, where M is the number of data points.

Display the first five entries of the table.

gps(1:5,:)

ans=5×4 table
       Timestamp        Latitude    Longitude    Altitude
    ________________    ________    _________    ________

    1461634424978430     45.532      -122.62      34.861 
    1461634425028360     45.532      -122.62       34.85 
    1461634425078181     45.532      -122.62      34.839 
    1461634425128114     45.532      -122.62      34.825 
    1461634425178370     45.532      -122.62      34.789

Convert the GPS coordinates to local east-north-up (ENU) coordinates by using the latlon2local function. The transformed coordinates define the waypoints of the ego vehicle. Units are in meters.

referenceLocation = [gps.Latitude(1) gps.Longitude(1) gps.Altitude(1)];
[gps.East,gps.North,gps.Up] = latlon2local(gps.Latitude,gps.Longitude,gps.Altitude,referenceLocation);

Calculate the yaw and velocity of the ego vehicle from the GPS data.

[yaw,velocity] = helperCalculateYawAndVelocity(gps,sim);
EgoData = table(gps.Timestamp,[gps.East,gps.North,gps.Up],velocity,yaw,VariableNames=["Time","Waypoints","Velocity","Yaw"]);

Display the first five entries of the EgoData table.

EgoData(1:5,:)

ans=5×4 table
          Time                    Waypoints                         Velocity                Yaw  
    ________________    ______________________________    ____________________________    _______

    1461634424978430         0           0           0         0          0          0    -13.289
    1461634425028360    1.2552    -0.39305     0.37473    27.078    -6.3955          0    -13.289
    1461634425078181    2.6257    -0.67587     0.11217    19.352    -4.2481          0    -12.381
    1461634425128114    3.5158    -0.91352      0.3314    31.264    -7.0961          0    -12.788
    1461634425178370    5.0913     -1.4249     0.26856     20.78    -12.254          0    -30.529

Raw GPS data often contains noise. In this example, you can smooth the noisy GPS waypoints by using a kinematic motion model and a window based statistical model. The kinematic motion model is preferred over the statistical method as it uses motion information to smooth the trajectory.

Smooth Ego Trajectory Using Motion Model

Create a smooth, jerk-limited trajectory from the ego waypoints by using the smoothTrajectory function. The generated ego trajectory features a smooth transition of accelerations between waypoints.

% Jerk tolerance
jerk = 0.1;
waypoints = EgoData.Waypoints;
speed = vecnorm(EgoData.Velocity,2,2);
yaw = EgoData.Yaw;
scenario.SampleTime = 0.05;
scenario = drivingScenario(SampleTime=scenario.SampleTime);
egoVehicle = vehicle(scenario,ClassID=1,Position=waypoints(1,:),Velocity=EgoData.Velocity(1,:),Yaw=yaw(1));

% Apply trajectory smoothing using smoothTrajectory
smoothTrajectory(egoVehicle,waypoints,Yaw=yaw,Jerk=jerk)
% Obtain smooth trajectory waypoints
reScenario = record(scenario);
for idx = 1:size(reScenario,2)
    smoothWaypoints(idx,:) = reScenario(idx).ActorPoses(1).Position;
end

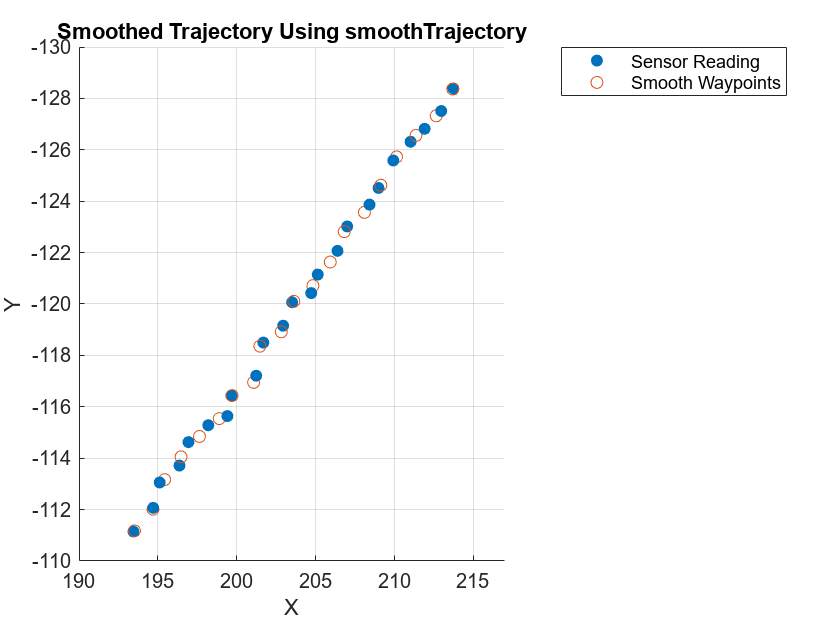
Visualize the smoothed ego trajectory. Note that this model is unable to smooth the trajectory because this is a high-frequency dataset. You can downsample the data and perform smoothing to reduce the error, but this can lead to data loss.

figure
scatterPlot1 = scatter3(waypoints(:,1),waypoints(:,2),waypoints(:,3),"filled");
hold on
scatterPlot2 = scatter3(smoothWaypoints(:,1),smoothWaypoints(:,2),smoothWaypoints(:,3));
hold off
view(0,270)
axis([190 217 -130 -110])
legend([scatterPlot1 scatterPlot2],{'Sensor Reading','Smooth Waypoints'})
title("Smoothed Trajectory Using smoothTrajectory")
xlabel("X")
ylabel("Y")
zlabel("Z")

Figure contains an axes object. The axes object with title Smoothed Trajectory Using smoothTrajectory contains 2 objects of type scatter. These objects represent Sensor Reading, Smooth Waypoints.

Smooth Ego Trajectory Using Statistical Model

Smooth the ego trajectory by using the smoothdata function. This function uses a statistical window-based, moving-average method to smooth the trajectory.

% The smoothData function smooths out x,y, and z separately
smoothFactor = 0.75; % Between 0 and 1
% sgolay smooths the waypoints using a Savitzky-Golay filter, which is more effective than other methods for varying data.
smoothWaypoints = smoothdata(waypoints(:,1:3),"sgolay",SmoothingFactor=smoothFactor');
% smoothdata can be further used to smooth yaw
smoothYaw = smoothdata(yaw,"sgolay",SmoothingFactor=smoothFactor);

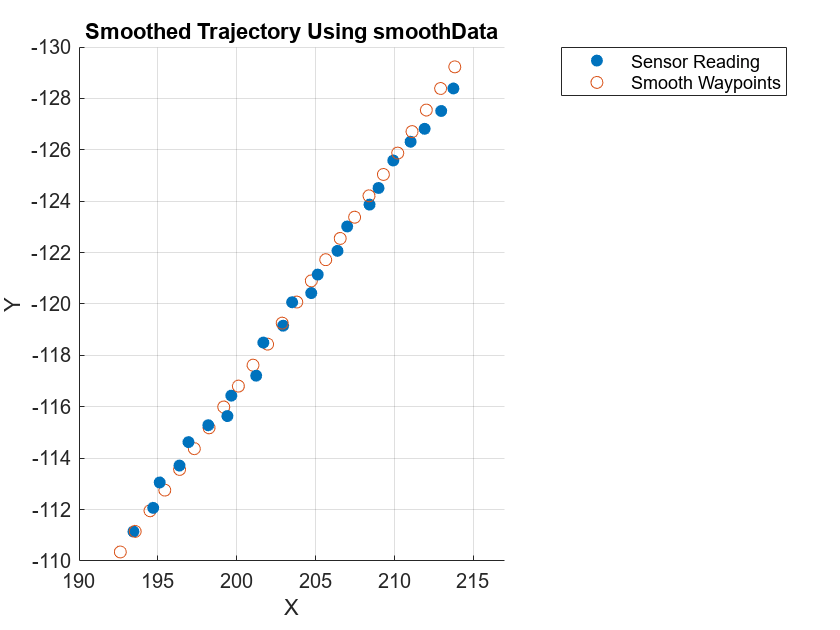
Visualize the smoothed trajectory. For high-frequency data, the smoothing results are better for the statistical model than for the motion model.

scatterPlot1 = scatter3(waypoints(:,1),waypoints(:,2),waypoints(:,3),"filled");
hold on
scatterPlot2 = scatter3(smoothWaypoints(:,1),smoothWaypoints(:,2),smoothWaypoints(:,3));
hold off
view(0,270)
axis([190 217 -130 -110])
legend([scatterPlot1 scatterPlot2],["Sensor Reading","Smooth Waypoints"])
title("Smoothed Trajectory Using smoothData")
xlabel("X")
ylabel("Y")
zlabel("Z")

Figure contains an axes object. The axes object with title Smoothed Trajectory Using smoothData contains 2 objects of type scatter. These objects represent Sensor Reading, Smooth Waypoints.

Helper Function

helperCalculateYawAndVelocity — Calculate yaw angles and velocity from the GPS and timestamp data.

function [calculatedYaw,calculatedVelocity] = helperCalculateYawAndVelocity(gps,sim)
% helperCalculateYawAndVelocity calculates yaw angles and velocity from the GPS and timestamp data
% This is a helper function for example purposes and may be removed or modified in the future.

% Copyright 2022 The MathWorks, Inc.
gps.relativeTime = double(gps.Timestamp - sim.startTime)/10^6;
gps.speed = helperComputeSpeed(gps.East,gps.North,gps.relativeTime);
sim.TotalTime = (sim.endTime - sim.startTime)/10^6;
importedScenario = drivingScenario(SampleTime=sim.egoSampleTime,StopTime=sim.TotalTime);
egoVehicleGPS = vehicle(importedScenario,ClassID=1,Position=[gps.East(1) gps.North(1) 0]);
trajectory(egoVehicleGPS,[gps.East gps.North zeros(size(gps,1),1)],gps.speed);
positionIndex = [1 3 6];
velocityIndex = [2 4 7];
i = 1;
while advance(importedScenario)
    position(1,:) = actorPoses(importedScenario).Position;
    simEgo.data(i,positionIndex) = position;
    velocity(1,:) = actorPoses(importedScenario).Velocity;
    simEgo.data(i,velocityIndex) = velocity;
    simEgo.data(i,5) = i;
    yaw = actorPoses(importedScenario).Yaw;
    simEgo.data(i,8) = yaw;
    simEgo.data(i,9) = importedScenario.SimulationTime;
    i = i + 1;
end
calculatedVelocity = [[0 0 0]; simEgo.data(:,velocityIndex)];
calculatedYaw = [simEgo.data(1,8); simEgo.data(:,8)];
end

Smooth GPS Waypoints for Ego Localization

Load and Preprocess GPS Data

Smooth Ego Trajectory Using Motion Model

Smooth Ego Trajectory Using Statistical Model

Helper Function

See Also

Functions

Related Topics