designRateConverter

Design multistage bandlimited sample rate converter System object

Since R2024b

Syntax

filtObj = designRateConverter(Name=Value)

Description

filtObj = designRateConverter(Name=Value) designs a multistage bandlimited sample-rate converter using one or more name-value arguments.

For example, filtObj = designRateConverter(InterpolationFactor=36,DecimationFactor=2,MaxStages=3,Bandwidth=1/72) designs a 36:2 or 18:1 rate converter with a maximum of three stages, and an input bandwidth of 1/72 in normalized frequency units. In normalized units, the input Nyquist frequency is set to 1 and bandwidth in this case is 1/72 of that Nyquist frequency. The function returns a three-stage cascade of dsp.FIRInterpolator objects each with an interpolation factor of 3, 2, and 3, respectively.

The designRateConverter function outputs the design configuration (number of stages and specifications of each stage) that has the least computational cost (number of multiplications per input sample). By default, the function estimates this cost and designs the default configuration based on this value.

When you specify only a partial list of filter parameters, the function designs the filter by setting the other design parameters to their default values. When you set Verbose = true, the function returns the values of all the design parameters and the effective conversion ratio.

example

Examples

collapse all

Design Multistage Decimator

Open Live Script

Design a multistage decimator with these specifications using the designRateConverter function:

Decimation factor of 36
Input bandwidth of interest set to 0.01 in normalized frequency units

Design the filter with MaxStages set to 2 and Inf. Setting MaxStages to 2 imposes the design to have a maximum of two stages. Setting MaxStages to Inf allows as many stages as needed to obtain an optimal design. Compare the cost of implementing the two filters.

Use the designRateConverter to design the multistage decimator. Set DecimationFactor to 36, Bandwidth to 0.01, and MaxStages to 2. Setting Verbose to true displays the default values of the other arguments the function uses.

decimTwoStages = designRateConverter(DecimationFactor=36,...
    Bandwidth=0.01,MaxStages=2,Verbose=true)

designRateConverter(InterpolationFactor=1, DecimationFactor=36, Bandwidth=0.01, StopbandAttenuation=80, MaxStages=2, CostMethod="estimate", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 1:36

decimTwoStages = 
  dsp.FilterCascade with properties:

         Stage1: [1x1 dsp.FIRDecimator]
         Stage2: [1x1 dsp.FIRDecimator]
    CloneStages: true

Design another filter by setting MaxStages to Inf. This setting chooses the optimal number of stages for the filter. The function designs the filter as a decimator cascade of three stages with decimation factors equal to 2, 3, and 3, respectively.

decimMaxStages = designRateConverter(DecimationFactor=36,MaxStages=Inf,...
    Bandwidth=0.01,Verbose=true)

designRateConverter(InterpolationFactor=1, DecimationFactor=36, Bandwidth=0.01, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 1:36

decimMaxStages = 
  dsp.FilterCascade with properties:

         Stage1: [1x1 dsp.FIRDecimator]
         Stage2: [1x1 dsp.FIRDecimator]
         Stage3: [1x1 dsp.FIRDecimator]
    CloneStages: true

View the filter information using the info function.

info(decimMaxStages)

ans = 
    'Discrete-Time Filter Cascade
     ----------------------------
     Number of stages: 3
     Stage cloning: enabled
     
     Stage1: dsp.FIRDecimator
     -------
     Discrete-Time FIR Multirate Filter (real)               
     -----------------------------------------               
     Filter Structure   : Direct-Form FIR Polyphase Decimator
     Decimation Factor  : 2                                  
     Polyphase Length   : 4                                  
     Filter Length      : 7                                  
     Stable             : Yes                                
     Linear Phase       : Yes (Type 1)                       
                                                             
     Arithmetic         : double                             
     
     
     Stage2: dsp.FIRDecimator
     -------
     Discrete-Time FIR Multirate Filter (real)               
     -----------------------------------------               
     Filter Structure   : Direct-Form FIR Polyphase Decimator
     Decimation Factor  : 2                                  
     Polyphase Length   : 6                                  
     Filter Length      : 11                                 
     Stable             : Yes                                
     Linear Phase       : Yes (Type 1)                       
                                                             
     Arithmetic         : double                             
     
     
     Stage3: dsp.FIRDecimator
     -------
     Discrete-Time FIR Multirate Filter (real)               
     -----------------------------------------               
     Filter Structure   : Direct-Form FIR Polyphase Decimator
     Decimation Factor  : 9                                  
     Polyphase Length   : 8                                  
     Filter Length      : 67                                 
     Stable             : Yes                                
     Linear Phase       : Yes (Type 1)                       
                                                             
     Arithmetic         : double                             
     
     '

Compare the Cost

Compare the cost of implementing the two filters. Notice that the cost on all metrics reduces when you remove the restriction on the maximum number of stages.

cost(decimTwoStages)

ans = struct with fields:
                  NumCoefficients: 130
                        NumStates: 132
    MultiplicationsPerInputSample: 5.9722
          AdditionsPerInputSample: 5.4444

cost(decimMaxStages)

ans = struct with fields:
                  NumCoefficients: 73
                        NumStates: 79
    MultiplicationsPerInputSample: 5.9444
          AdditionsPerInputSample: 5.1667

Compare the Magnitude Response

Comparing the magnitude response of the two filters. Both the filters have the same transition-band behavior and follow the design specifications.

filterAnalyzer(decimTwoStages,decimMaxStages,FilterNames=["TwoStages","ThreeStages"])

However, to understand where the computational savings are coming from in the three-stage design, look at the magnitude response of the three stages individually.

stage1 = decimMaxStages.Stage1

stage1 = 
  dsp.FIRDecimator with properties:

   Main
    DecimationFactor: 2
     NumeratorSource: 'Property'
           Numerator: [-0.0317 0 0.2817 0.5000 0.2817 0 -0.0317]
           Structure: 'Direct form'

  Use get to show all properties

stage2 = decimMaxStages.Stage2

stage2 = 
  dsp.FIRDecimator with properties:

   Main
    DecimationFactor: 2
     NumeratorSource: 'Property'
           Numerator: [0.0065 0 -0.0507 0 0.2942 0.5000 0.2942 0 -0.0507 0 0.0065]
           Structure: 'Direct form'

  Use get to show all properties

stage3 = decimMaxStages.Stage3

stage3 = 
  dsp.FIRDecimator with properties:

   Main
    DecimationFactor: 9
     NumeratorSource: 'Property'
           Numerator: [-9.6325e-05 -1.5539e-04 -2.4072e-04 -3.0942e-04 -3.2259e-04 -2.3401e-04 0 4.0676e-04 9.8161e-04 0.0017 0.0024 0.0029 0.0032 0.0029 0.0018 0 -0.0026 -0.0058 -0.0092 -0.0123 -0.0145 -0.0149 -0.0129 -0.0081 0 0.0113 ... ] (1x67 double)
           Structure: 'Direct form'

  Use get to show all properties

The third stage provides the narrow transition width required for the overall design. However, the third stage contains spectral replicas. The first stage removes such replicas. The first and second stages operate at a faster rate but can afford a wider transition width. The result is a decimate-by-2 first stage filter with only 5 nonzero coefficients and decimate-by-2 second stage filter with only 7 nonzero coefficients. The third stage contains 61 nonzero coefficients. Overall, the three-stage design uses 73 nonzero coefficients while the two-stage design uses 130 nonzero coefficients.

filterAnalyzer(stage1,stage2,stage3,FilterNames=["Stage1","Stage2","Stage3"])

Design Multistage Interpolator with Different Cost Methods

Open Live Script

Design a multistage interpolator with these specifications using the designRateConverter function:

Interpolation factor of 23
Input bandwidth of interest set to 0.1 in normalized frequency units

Design the filter with CostMethod set to "estimate" and "design". Compare the cost of the two designs.

Use the designRateConverter to design the multistage interpolator. Set InterpolationFactor to 128 and Bandwidth to 0.1. Setting Verbose to true displays the default values of the other arguments the function uses. Notice that by default the function sets the CostMethod to "estimate". The function determines the design configuration (number of stages and specifications for each stage) based on the estimated cost.

interpEstimateCost = designRateConverter(InterpolationFactor=128,...
    Bandwidth=0.1,Verbose=true)

designRateConverter(InterpolationFactor=128, DecimationFactor=1, Bandwidth=0.1, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 128:1

interpEstimateCost = 
  dsp.FilterCascade with properties:

         Stage1: [1x1 dsp.FIRInterpolator]
         Stage2: [1x1 dsp.FIRInterpolator]
         Stage3: [1x1 dsp.FIRInterpolator]
    CloneStages: true

Change CostMethod to "design". The function optimizes the design with respect to the exact cost rather than the estimated cost. Notice that the design now uses four stages.

interpDesignCost = designRateConverter(InterpolationFactor=128,...
    Bandwidth=0.1,CostMethod="design",Verbose=true)

designRateConverter(InterpolationFactor=128, DecimationFactor=1, Bandwidth=0.1, StopbandAttenuation=80, MaxStages=Inf, CostMethod="design", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 128:1

interpDesignCost = 
  dsp.FilterCascade with properties:

         Stage1: [1x1 dsp.FIRInterpolator]
         Stage2: [1x1 dsp.FIRInterpolator]
         Stage3: [1x1 dsp.FIRInterpolator]
         Stage4: [1x1 dsp.FIRInterpolator]
    CloneStages: true

Compare the Cost

Compute the cost of implementing the two filters. When you set CostMethod to "estimate", the function finds a sub-optimal solution. Setting CostMethod to "design" allows the function to obtain an optimal solution, at the expense of the runtime of the design algorithm.

cost(interpEstimateCost)

ans = struct with fields:
                  NumCoefficients: 170
                        NumStates: 11
    MultiplicationsPerInputSample: 546
          AdditionsPerInputSample: 419

cost(interpDesignCost)

ans = struct with fields:
                  NumCoefficients: 92
                        NumStates: 14
    MultiplicationsPerInputSample: 528
          AdditionsPerInputSample: 401

Compare the Magnitude Response

Compare the magnitude response. Both filters have the same transition-band behavior but different stopband behavior.

filterAnalyzer(interpEstimateCost,interpDesignCost,FilterNames=["Estimate","Design"])

Design Multistage Sample-Rate Converter with Varying Tolerance Values

Open Live Script

Design a multistage sample-rate converter with these specifications using the designRateConverter function:

Input sample rate of 48 kHz
Output sample rate of 44.1 kHz

Change the output tolerance of the design from 0 Hz up to 220 Hz. This allows the output sample rate to be different than the specified 44.1 kHz by up to 220 Hz. Compare the cost of implementing the two filters.

Use the designRateConverter to design the multistage sample-rate converter. Set InputSampleRate to 48 kHz, OutputSampleRate to 44.1 kHz, and Tolerance to 0. Setting Verbose to true displays the default values of the other arguments the function uses.

The function uses an effective conversion ratio of 147:160, which is high.

designExactRate = designRateConverter(InputSampleRate=48e3,OutputSampleRate=44.1e3,...
    Tolerance=0,Verbose=true)

designRateConverter(InputSampleRate=48000, OutputSampleRate=44100, Bandwidth=17640, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 147:160
Input sample rate: 48000
Output sample rate: 44100

designExactRate = 
  dsp.FIRRateConverter with properties:

   Main
    InterpolationFactor: 147
       DecimationFactor: 160
        NumeratorSource: 'Property'
              Numerator: [6.1512e-05 6.2675e-05 6.3826e-05 6.4965e-05 6.6092e-05 6.7203e-05 6.8300e-05 6.9379e-05 7.0441e-05 7.1484e-05 7.2507e-05 7.3508e-05 7.4487e-05 7.5442e-05 7.6372e-05 7.7276e-05 7.8153e-05 7.9001e-05 ... ] (1x4017 double)

  Use get to show all properties

Allow a tolerance of 220 Hz. The function now uses an effective conversion ratio of 11:12 which has less computational complexity.

designApproximateRate = designRateConverter(InputSampleRate=48e3,OutputSampleRate=44.1e3,...
    Tolerance=220,Verbose=true)

designRateConverter(InputSampleRate=48000, OutputSampleRate=44100, Bandwidth=17600, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=220, ToleranceUnits="absolute")

Conversion ratio: 11:12
Input sample rate: 48000
Output sample rate: 44100 (specified) 44000 (effective)

designApproximateRate = 
  dsp.FIRRateConverter with properties:

   Main
    InterpolationFactor: 11
       DecimationFactor: 12
        NumeratorSource: 'Property'
              Numerator: [3.8374e-05 5.7656e-05 7.7489e-05 9.5302e-05 1.0809e-04 1.1269e-04 1.0611e-04 8.5908e-05 5.0600e-05 0 -6.4471e-05 -1.3962e-04 -2.2046e-04 -3.0037e-04 -3.7143e-04 -4.2502e-04 -4.5247e-04 -4.4592e-04 -3.9922e-04 ... ] (1x307 double)

  Use get to show all properties

Compare the Cost

Compute the cost of implementing the two filters. Allowing some tolerance in the output sample rate reduces the cost of the filter.

cost(designExactRate)

ans = struct with fields:
                  NumCoefficients: 3993
                        NumStates: 27
    MultiplicationsPerInputSample: 24.9563
          AdditionsPerInputSample: 24.0375

cost(designApproximateRate)

ans = struct with fields:
                  NumCoefficients: 283
                        NumStates: 27
    MultiplicationsPerInputSample: 23.5833
          AdditionsPerInputSample: 22.6667

Compare the Magnitude Response and Group Delay

Compare the magnitude response of the two filters. The filter with zero tolerance has a very narrow transition width while allowing some tolerance increases the transition width and the passband width.

filterAnalyzer(designExactRate,designApproximateRate,FilterNames=["ZeroTolerance","HigherTolerance"])

Compare the group delay of the two filters. The filter with zero tolerance has a group delay of 2008 samples while the allowing some tolerance decreases the group delay significantly to 153.

grpdelay(designExactRate)

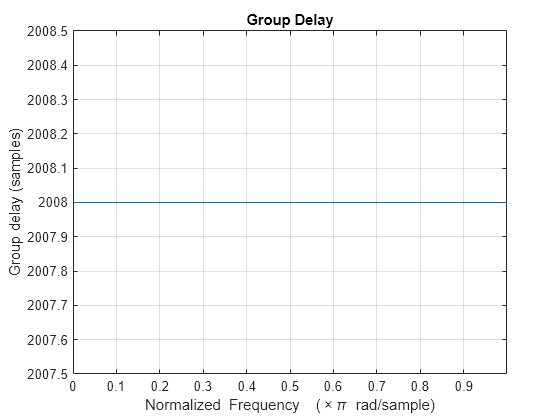
Figure contains an axes object. The axes object with title Group Delay, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Group delay (samples) contains an object of type line.

grpdelay(designApproximateRate)

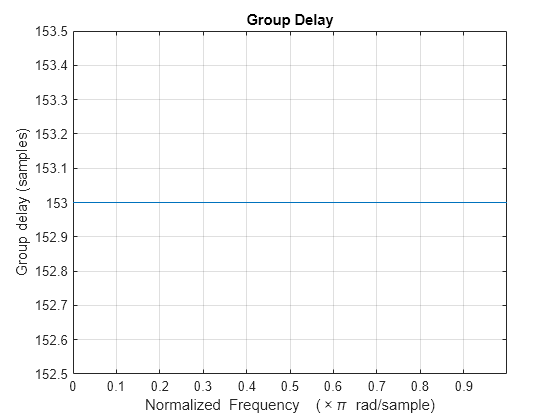
Figure contains an axes object. The axes object with title Group Delay, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Group delay (samples) contains an object of type line.

Design Multistage Sample-Rate Converter by Specifying Tolerance in Percentage

Open Live Script

Design a multistage sample-rate converter with these specifications using the designRateConverter function:

Interpolation factor of 3756
Decimation factor of 6200

Change the tolerance of the design from 0 to 0.1% to 1%. Compare the cost of implementing these filters.

Use the designRateConverter to design the multistage sample-rate converter. Set InterpolationFactor to 3756, DecimationFactor to 6200, and ToleranceUnits to "percentage". The default value of Tolerance is 0. Setting Verbose to true displays the default values of the other arguments the function uses.

The function uses an effective conversion ratio of 939:1550 since it removes the common denominator 4 from the specified conversion ratio 3756:6200.

designExactRate = designRateConverter(InterpolationFactor=3756,...
    DecimationFactor=6200,ToleranceUnits="percentage",...
    Verbose=true)

designRateConverter(InterpolationFactor=3756, DecimationFactor=6200, Bandwidth=0.48464516129032265, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=0, ToleranceUnits="percentage")

Conversion ratio: 3756:6200 (specified), 939:1550 (effective)

designExactRate = 
  dsp.FIRRateConverter with properties:

   Main
    InterpolationFactor: 939
       DecimationFactor: 1550
        NumeratorSource: 'Property'
              Numerator: [4.0641e-05 4.0719e-05 4.0798e-05 4.0876e-05 4.0955e-05 4.1033e-05 4.1111e-05 4.1190e-05 4.1268e-05 4.1346e-05 4.1424e-05 4.1502e-05 4.1580e-05 4.1657e-05 4.1735e-05 4.1813e-05 4.1890e-05 4.1967e-05 4.2045e-05 … ] (1×38895 double)

  Show all properties

Set Tolerance to 0.1%. The effective conversion ratio changes to 20:33, which is very close to the requested ratio 3756/6200. Indeed, 3756/6200-20/33 = 2.5415e-04, which is within the allowed tolerance of 1e-3 (i.e 0.1%).

designApproxRate = designRateConverter(InterpolationFactor=3756,...
    DecimationFactor=6200,ToleranceUnits="percentage",...
    Tolerance=0.1,Verbose=true)

designRateConverter(InterpolationFactor=3756, DecimationFactor=6200, Bandwidth=0.48484848484848486, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=0.1, ToleranceUnits="percentage")

Conversion ratio: 3756:6200 (specified), 20:33 (effective)

designApproxRate = 
  dsp.FIRRateConverter with properties:

   Main
    InterpolationFactor: 20
       DecimationFactor: 33
        NumeratorSource: 'Property'
              Numerator: [2.7533e-05 3.2037e-05 3.6669e-05 4.1362e-05 4.6039e-05 5.0621e-05 5.5019e-05 5.9141e-05 6.2891e-05 6.6170e-05 6.8878e-05 7.0914e-05 7.2179e-05 7.2576e-05 7.2015e-05 7.0409e-05 6.7680e-05 6.3762e-05 5.8596e-05 … ] (1×841 double)

  Show all properties

Further increase the tolerance to 1%. The effective conversion ratio further reduces to 3:5. Note that 3756/6200-3/5 = 0.0058 which is within the allowed tolerance of 0.01 (i.e. 1%).

designApproxRateHigherTol = designRateConverter(InterpolationFactor=3756,...
    DecimationFactor=6200,ToleranceUnits="percentage",...
    Tolerance=1,Verbose=true)

designRateConverter(InterpolationFactor=3756, DecimationFactor=6200, Bandwidth=0.48, StopbandAttenuation=80, MaxStages=Inf, CostMethod="estimate", Tolerance=1, ToleranceUnits="percentage")

Conversion ratio: 3756:6200 (specified), 3:5 (effective)

designApproxRateHigherTol = 
  dsp.FIRRateConverter with properties:

   Main
    InterpolationFactor: 3
       DecimationFactor: 5
        NumeratorSource: 'Property'
              Numerator: [2.0191e-05 5.1900e-05 7.6263e-05 6.5863e-05 0 -1.1657e-04 -2.4237e-04 -3.0607e-04 -2.3543e-04 0 3.5191e-04 6.8589e-04 8.1926e-04 6.0023e-04 0 -8.2688e-04 -0.0016 -0.0018 -0.0013 0 0.0017 0.0031 0.0035 0.0024 0 … ] (1×129 double)

  Show all properties

Compare the Cost

Compute the cost of implementing these filters. As you increase the tolerance, the computational complexity of the filter reduces.

cost(designExactRate)

ans = struct with fields:
                  NumCoefficients: 38871
                        NumStates: 41
    MultiplicationsPerInputSample: 25.0781
          AdditionsPerInputSample: 24.4723

cost(designApproxRate)

ans = struct with fields:
                  NumCoefficients: 817
                        NumStates: 42
    MultiplicationsPerInputSample: 24.7576
          AdditionsPerInputSample: 24.1515

cost(designApproxRateHigherTol)

ans = struct with fields:
                  NumCoefficients: 105
                        NumStates: 42
    MultiplicationsPerInputSample: 21
          AdditionsPerInputSample: 20.4000

Compare the Magnitude Response and Group Delay

Compare the magnitude response of the filters. The filter with zero tolerance has the least transition width and the transition width increases as the tolerance increases.

filterAnalyzer(designExactRate,designApproxRate,designApproxRateHigherTol,...
    FilterNames=["ZeroTolerance","OneTenthPercentTolerance","OnePercentTolerance"])

Comparing the group delay values, you can see that the filter with zero tolerance has a significantly higher group delay of 19447.1 samples. As tolerance increases, the group delay reduces. For a tolerance of 1%, the group delay reduces to 64 samples.

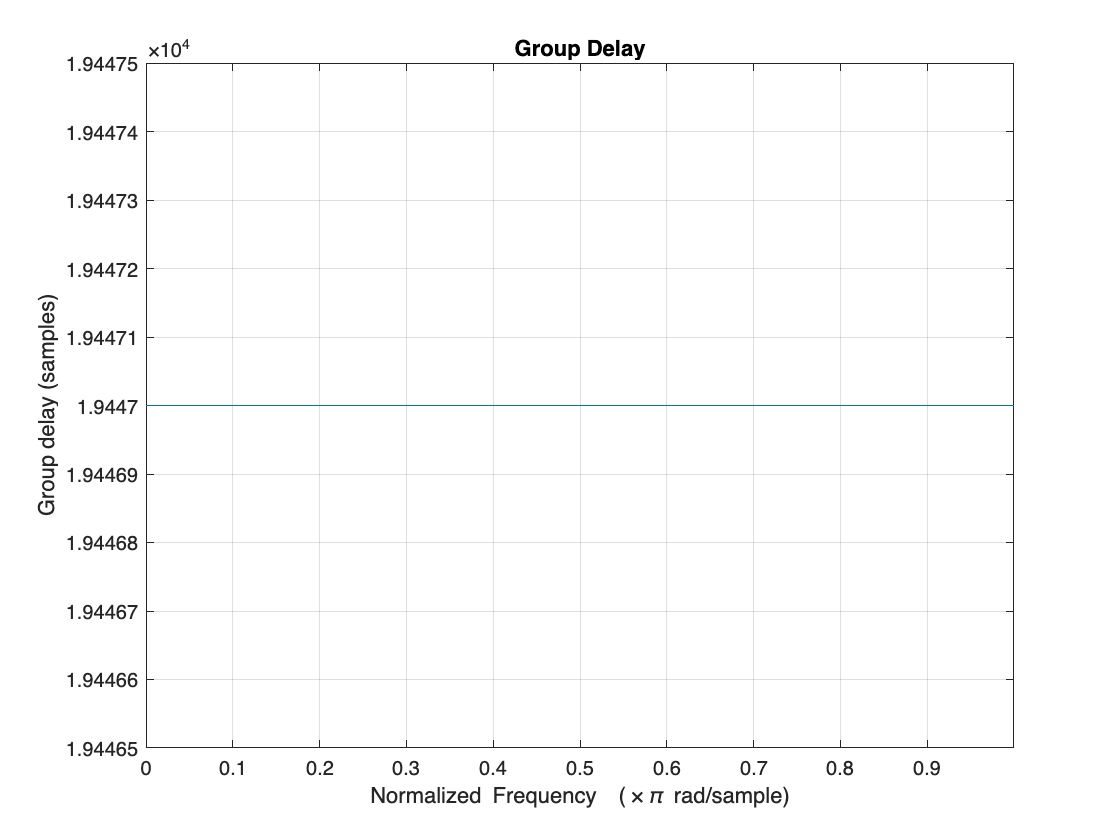
grpdelay(designExactRate)

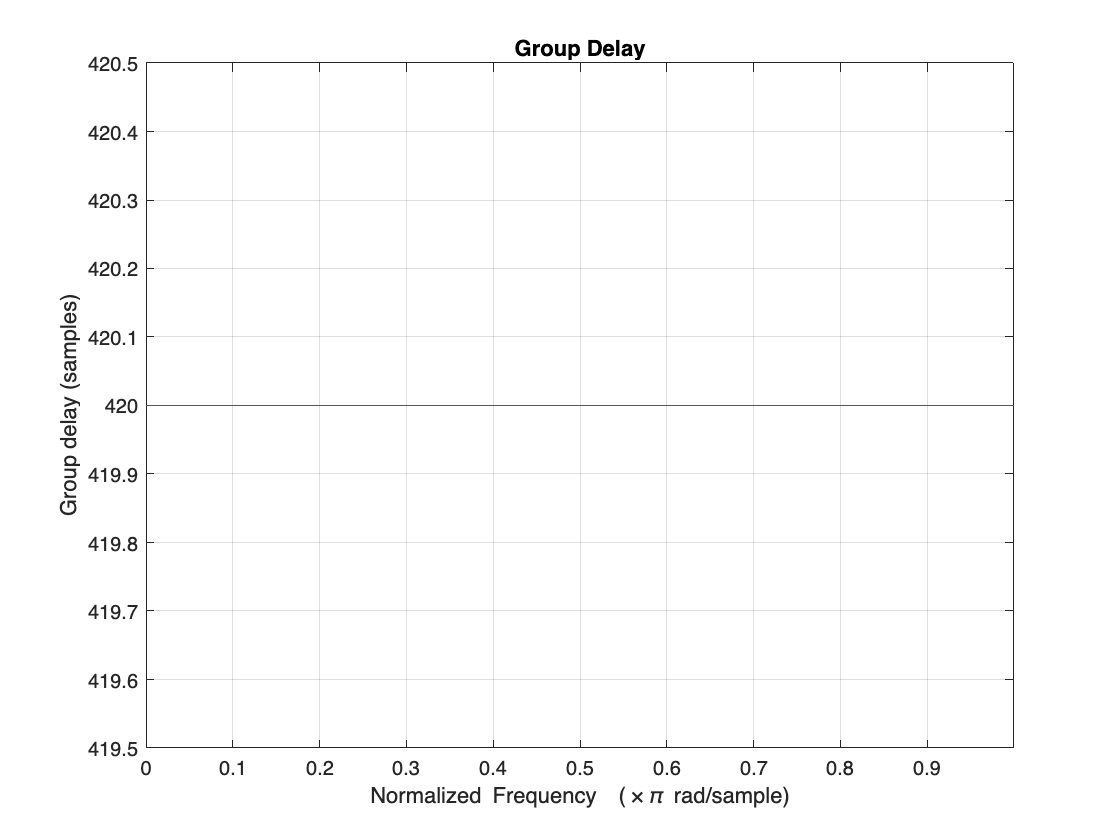
Figure contains an axes object. The axes object with title Group Delay, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Group delay (samples) contains an object of type line.

grpdelay(designApproxRate)

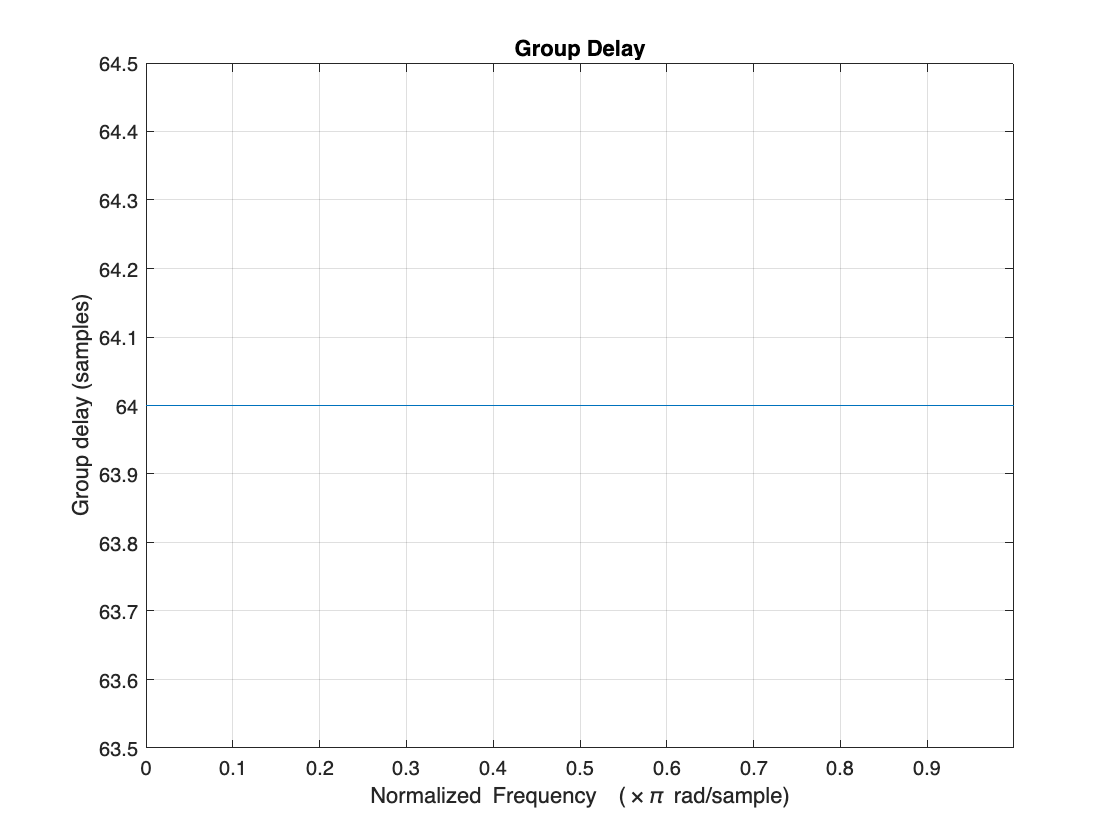
Figure contains an axes object. The axes object with title Group Delay, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Group delay (samples) contains an object of type line.

grpdelay(designApproxRateHigherTol)

Figure contains an axes object. The axes object with title Group Delay, xlabel Normalized Frequency ( times pi blank rad/sample), ylabel Group delay (samples) contains an object of type line.

Input Arguments

collapse all

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: filtObj = designRateConverter(InterpolationFactor=36,DecimationFactor=2,StopbandAttenuation=90,MaxStages=3,Bandwidth=1/72)

`InterpolationFactor` — Target interpolation factor
`1` (default) | positive integer

Target interpolation factor L, specified as a positive integer.

When you specify the interpolation and decimation factors L and M, the function derives the effective conversion ratio from the rational approximation of L/M subject to approximation tolerance Tol. For example, if L/M is 77/2223 = 0.0346, the function approximates this ratio to 1/29 = 0.0345 if you allow a tolerance Tol of 1% from the original ratio.

Furthermore, the function removes the common denominator between L and M, if any. For example, if L is 24 and M is 9, the effective conversion ratio is 8/3.

When you specify the input sample rate FsIn, the output sample rate FsOut, or both, the function uses frequency values in Hz. When you specify neither the input sample rate nor the output sample rate, the function uses normalized frequency units.

Data Types: single | double

`DecimationFactor` — Target decimation factor
`1` (default) | positive integer

Target decimation factor M, specified as a positive integer.

Furthermore, the function removes the common denominator between L and M, if any. For example, if L is 24 and M is 9, the effective conversion ratio is 8/3.

Data Types: single | double

`InputSampleRate` — Input sample rate
positive scalar

Input sample rate FsIn, specified as a positive scalar. When you specify the input and output sample rates, the function derives the conversion ratio from the rational approximation of FsOut/FsIn subject to approximation tolerance Tol.

When you specify one or both of input sample rate and output sample rate, the function uses frequency values in Hz.

Data Types: single | double

`OutputSampleRate` — Output sample rate
positive scalar

Output sample rate FsOut, specified as a positive scalar. When you specify the input and output sample rates, the function derives the conversion ratio from the rational approximation of FsOut/FsIn subject to approximation tolerance Tol.

When you specify one or both of input sample rate and output sample rate, the function uses frequency values in Hz.

Data Types: single | double

`Tolerance` — Tolerance of conversion ratio or rate approximation
`0` (default) | nonnegative scalar

Tolerance of conversion ratio or rate approximation, specified as a nonnegative scalar.

The designRateConverter function can use the exact conversion ratio or an approximation of the conversion ratio which has lower values of interpolation and decimation factors. For example, with a tolerance of 10%, the function approximates the conversion ratio 202:301 as 2:3. The ratio 2:3 is the effective conversion ratio. When you specify the rate conversion factors, L and M, and do not specify the input sample rate FsIn or the output sample rate FsOut, the function performs the approximation directly on the specified conversion ratio L/M. When you specify FsIn or FsOut in addition, the function approximates these parameters instead. For more information, see the following table.

In each combination of specification parameters, the function adjusts the target parameter while applying the tolerance. The table shows how the function determines the effective conversion ratio and effective sample rate based on the combination of specification parameters. The table also shows the upper bound you can specify on tolerance value based on the specification parameters you choose.

Specification Parameters	Target Parameter Approximation			Tolerance Units	Effective Conversion Factors	Upper Bound On Tolerance
	Target Parameter	Nominal Value of Target Parameter	Adjusted Value of Target Parameter
L,M	L/M ratio (user-specified)	L/M	Leff/Meff	`"absolute"`	`[Leff,Meff] = rat(L/M,Tolerance)`	L/M
L,M	L/M ratio (user-specified)	L/M	Leff/Meff	`"percentage"`	`[Leff,Meff] = rat(L/M,((Tolerance/100)*L)/M)`	`100`
L,M,FsIn	FsOut (derived from L, M, and FsIn)	FsIn×L/M	FsIn×Leff/Meff	`"absolute"`	`[Leff,Meff] = rat(L/M,Tolerance/FsIn)`	FsIn×L/M
L,M,FsIn	FsOut (derived from L, M, and FsIn)	FsIn×L/M	FsIn×Leff/Meff	`"percentage"`	`[Leff,Meff] = rat(L,M,((Tolerance/100)*L)/M)`	`100`
L,M,FsOut	FsIn (derived from L, M, and FsOut)	FsOut×M/L	FsOut×Meff/Leff	`"absolute"`	`[Leff,Meff] = rat(M/L,Tolerance/FsOut)`	FsOut×M/L
L,M,FsOut	FsIn (derived from L, M, and FsOut)	FsOut×M/L	FsOut×Meff/Leff	`"percentage"`	`[Leff,Meff] = rat(M/L,((Tolerance/100)*M)/L)`	`100`
FsIn,FsOut	FsOut (user-specified)	FsOut	FsIn×Leff/Meff	`"absolute"`	`[Leff,Meff] = rat(FsOut/FsIn,(FsOut+Tolerance)/FsIn-delta)`	FsOut
FsIn,FsOut	FsOut (user-specified)	FsOut	FsIn×Leff/Meff	`"percentage"`	`[Leff,Meff] = rat(FsOut/FsIn,(FsOut+(Tolerance/100)*FsOut)/FsIn-delta)`	`100`

where,

L is the interpolation factor that you specify in InterpolationFactor.
M is the decimation factor that you specify in DecimationFactor.
FsIn is the input sample rate that you specify in InputSampleRate.
FsOut is the output sample rate that you specify in OutputSampleRate.
Leff/Meff is the effective conversion ratio the function uses to design the rate converter.
delta is Le/Me, where [Le,Me] = rat(FsOut/FsIn,0).

Data Types: single | double

`ToleranceUnits` — Units of tolerance
`"absolute"` (default) | `"percentage"`

Units of tolerance, specified as one of these options:

"absolute" –– Specify tolerance in Hz.
"percentage" ––- Specify tolerance as a percentage (%).

For more information on how the tolerance units affect the effective conversion ratio and the upper bound on tolerance, see the Tolerance argument description.

Data Types: char | string

`Bandwidth` — One-sided input bandwidth of interest
`0.8` (default) | real scalar

One-sided input bandwidth of interest, specified as a real scalar in Hz or in normalized frequency units.

When you specify the input sample rate FsIn, the output sample rate FsOut, or both, Bandwidth uses Hz units and the default value is given by 0.8×min(FsIn,FsOut)/2 Hz.

When you specify neither the input sample rate nor the output sample rate, Bandwidth uses normalized frequency units and the default value is given by 0.8×min(L/M,1).

Data Types: single | double

`StopbandAttenuation` — Target stopband attenuation
`80` (default) | real positive scalar

Target stopband attenuation Astop used in each stage, specified as a real positive scalar in dB.

Data Types: single | double

`MaxStages` — Maximum number of design stages
`Inf` (default) | positive integer

Maximum number of design stages, specified as Inf or a positive integer. The actual design can have fewer stages than the value of MaxStages you specify in this argument.

Data Types: single | double

`CostMethod` — Method to determine computational cost
`"estimate"` (default) | `"design"`

Method to determine computational cost, specified as one of these:

"estimate" –– The minimization objective uses the estimated cost of the configurations, that is, the sum of estimated cost of all stages instead of the exact cost. This method is faster but can result in a suboptimal configuration.
"design" –– The minimization objective uses the true cost of the configurations, that is, the sum of true cost of all stages. This method takes longer time to design the filter but results in an optimal configuration.

Data Types: char | string

`Verbose` — Option to print function call in MATLAB^®
`false` (default) | `true`

Option to print the entire function call in MATLAB, specified as one of these:

false –– The function does not print the function call.
true –– The function prints the entire function call including the default values of the Name=Value arguments that you did not specify when calling the function. The function also returns the effective conversion ratio.
Use this argument to view all the values used by the function to design the rate converter.

Data Types: logical

Output Arguments

collapse all

`filtObj` — Sample rate converter object
`dsp.FIRRateConverter` | `dsp.FIRDecimatordsp.FIRInterpolator` | `dsp.FilterCascade` | `dsp.FIRFilter`

Sample rate converter object, returned as one of these:

dsp.FIRRateConverter –– Single-stage design when you specify L and M > 1.
dsp.FIRDecimator –– Single-stage decimation when you specify L = 1 and M > 1.
dsp.FIRInterpolator –– Single-stage interpolation when you specify L > 1 and M = 1.
dsp.FilterCascade –– All multistage designs.
dsp.FIRFilter –– When you specify L = 1 and M = 1.

Algorithms

The function splits the overall interpolation and decimation factors into smaller factors with each factor corresponding to the individual stage. The combined rate conversion factor of all the individual stages must equal the overall rate conversion factor. The combined response must meet or exceed the given design specifications.

The function determines the number of stages and the sequence of stages based on the overall implementation cost. The function chooses the configuration that has the least implementation cost. Depending on the setting of CostMethod, the function estimates the cost or determines it exactly of a specific design configuration or determines it exactly. The estimation method is faster but can lead to suboptimal designs. The design method takes longer but gives an accurate overall cost of implementation.

Version History

Introduced in R2024b

designRateConverter

Syntax

Description

Examples

Design Multistage Decimator

Design Multistage Interpolator with Different Cost Methods

Design Multistage Sample-Rate Converter with Varying Tolerance Values

Design Multistage Sample-Rate Converter by Specifying Tolerance in Percentage

Input Arguments

Name-Value Arguments

`InterpolationFactor` — Target interpolation factor
`1` (default) | positive integer

`DecimationFactor` — Target decimation factor
`1` (default) | positive integer

`InputSampleRate` — Input sample rate
positive scalar

`OutputSampleRate` — Output sample rate
positive scalar

`Tolerance` — Tolerance of conversion ratio or rate approximation
`0` (default) | nonnegative scalar

`ToleranceUnits` — Units of tolerance
`"absolute"` (default) | `"percentage"`

`Bandwidth` — One-sided input bandwidth of interest
`0.8` (default) | real scalar

`StopbandAttenuation` — Target stopband attenuation
`80` (default) | real positive scalar

`MaxStages` — Maximum number of design stages
`Inf` (default) | positive integer

`CostMethod` — Method to determine computational cost
`"estimate"` (default) | `"design"`

`Verbose` — Option to print function call in MATLAB^®
`false` (default) | `true`

Output Arguments

`filtObj` — Sample rate converter object
`dsp.FIRRateConverter` | `dsp.FIRDecimatordsp.FIRInterpolator` | `dsp.FilterCascade` | `dsp.FIRFilter`

Algorithms

Version History

See Also

Objects

designRateConverter

Syntax

Description

Examples

Design Multistage Decimator

Design Multistage Interpolator with Different Cost Methods

Design Multistage Sample-Rate Converter with Varying Tolerance Values

Design Multistage Sample-Rate Converter by Specifying Tolerance in Percentage

Input Arguments

Name-Value Arguments

InterpolationFactor — Target interpolation factor 1 (default) | positive integer

DecimationFactor — Target decimation factor 1 (default) | positive integer

InputSampleRate — Input sample rate positive scalar

OutputSampleRate — Output sample rate positive scalar

Tolerance — Tolerance of conversion ratio or rate approximation 0 (default) | nonnegative scalar

ToleranceUnits — Units of tolerance "absolute" (default) | "percentage"

Bandwidth — One-sided input bandwidth of interest 0.8 (default) | real scalar

StopbandAttenuation — Target stopband attenuation 80 (default) | real positive scalar

MaxStages — Maximum number of design stages Inf (default) | positive integer

CostMethod — Method to determine computational cost "estimate" (default) | "design"

Verbose — Option to print function call in MATLAB® false (default) | true

Output Arguments

filtObj — Sample rate converter object dsp.FIRRateConverter | dsp.FIRDecimatordsp.FIRInterpolator | dsp.FilterCascade | dsp.FIRFilter

Algorithms

Version History

See Also

Objects

`InterpolationFactor` — Target interpolation factor
`1` (default) | positive integer

`DecimationFactor` — Target decimation factor
`1` (default) | positive integer

`InputSampleRate` — Input sample rate
positive scalar

`OutputSampleRate` — Output sample rate
positive scalar

`Tolerance` — Tolerance of conversion ratio or rate approximation
`0` (default) | nonnegative scalar

`ToleranceUnits` — Units of tolerance
`"absolute"` (default) | `"percentage"`

`Bandwidth` — One-sided input bandwidth of interest
`0.8` (default) | real scalar

`StopbandAttenuation` — Target stopband attenuation
`80` (default) | real positive scalar

`MaxStages` — Maximum number of design stages
`Inf` (default) | positive integer

`CostMethod` — Method to determine computational cost
`"estimate"` (default) | `"design"`

`Verbose` — Option to print function call in MATLAB^®
`false` (default) | `true`

`filtObj` — Sample rate converter object
`dsp.FIRRateConverter` | `dsp.FIRDecimatordsp.FIRInterpolator` | `dsp.FilterCascade` | `dsp.FIRFilter`