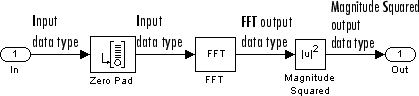
Magnitude FFT

Compute nonparametric estimate of spectrum using periodogram method

Libraries:
DSP System Toolbox / Estimation / Power Spectrum Estimation
DSP System Toolbox / Transforms / Power Spectrum Estimation

Description

The Magnitude FFT block computes a nonparametric estimate of the spectrum using the periodogram method.

Ports

Input

expand all

Input — Input
vector | matrix

Specify the input u to the block as a vector or a matrix of size M-by-N.

The block treats an M-by-N matrix input as M sequential time samples from N independent channels.

The Magnitude FFT block supports real and complex floating-point inputs. The block also supports real fixed-point inputs in the Magnitude and Magnitude squared modes, and complex fixed-point inputs in the Magnitude squared mode.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

Output

expand all

Output — Magnitude FFT output
vector | matrix

Magnitude FFT output, returned as a vector or a matrix.

The block computes a separate estimate for each of the N independent channels and generates an N_fft-by-N matrix output. Each column of the output matrix contains the estimate of the power spectral density of the corresponding input column at N_fft equally spaced frequency points in the range [0,F_s), where F_s represents the sample rate of the signal.

When you set the Output parameter to Magnitude squared, the block output for an M-by-N input u is equivalent to:

y = abs(fft(u,nfft)).^2	% M ≤ nfft

When you set the Output parameter to Magnitude, the block output for an input u is equivalent to:

y = abs(fft(u,nfft)) 	  % M ≤ nfft

When M > N_fft, the block wraps the input to N_fft before computing the FFT using one of the above equations:

y(:,k) = datawrap(u(:,k),nfft)  % 1 ≤ k ≤ N

When M > N_fft, the block can also truncate the input:

y(:,k) = abs(fft(u,nfft)) 	% 1 ≤ k ≤ N

Data Types: single | double | int8 | int16 | int32 | fixed point

Parameters

expand all

Output — Type of output
`Magnitude squared` (default) | `Magnitude`

Specify whether the block computes the magnitude FFT or the magnitude-squared FFT of the input signal. For more details on how this block computes the output based on this setting, see the Output port description.

FFT implementation — FFT implementation
`Auto` (default) | `Radix-2` | `FFTW`

Set this parameter to one of these values:

Auto –– Use this option to let the block choose the FFT implementation. For transform lengths that are not a power of 2, the block restricts the generated code to MATLAB^® host computers.
Radix-2 –– Use this option for bit-reversed processing, fixed or floating-point data, or for portable C-code generation using Simulink^® Coder™. The first dimension M of the input matrix must be a power of two. To work with other input sizes, use the Pad block to pad or truncate the dimensions to powers of two, or if possible choose the FFTW algorithm.
FFTW –– Use this option to support an input signal of arbitrary length. The block restricts the generated code with the FFTW implementation to MATLAB host computers.

Inherit FFT length from input dimensions — Inherit FFT length from input frame size
`off` (default) | `on`

Select this parameter to use the input frame size as the number of data points on which to perform the FFT. When you select this check box, the input frame size must be a power of two. When you do not select this check box, the FFT length parameter specifies the number of data points.

FFT length — FFT length
`256` (default) | positive integer

Enter the number of data points N_fft on which to perform the FFT. When N_fft is larger than the input frame size, the block pads each frame with zeros as needed. When N_fft is smaller than the input frame size, the block wraps each frame as needed.

When you set the FFT implementation parameter to Radix-2, this value must be a power of 2.

Dependency

To enable this parameter, clear the Inherit FFT length from input dimensions parameter.

Wrap input data when FFT length is shorter than input length — Choose to wrap or truncate input
`on` (default) | `off`

Choose to wrap or truncate the input depending on the FFT length.

When you select this parameter and if the FFT length is shorter than the input length, a modulo-length data wrapping occurs before the FFT operation. When you clear this parameter, the block truncates the input data to the FFT length before the FFT operation.

Block Characteristics

Data Types	`double` \| `fixed point` \| `integer` \| `single`
Direct Feedthrough	`no`
Multidimensional Signals	`no`
Variable-Size Signals	`no`
Zero-Crossing Detection	`no`

More About

expand all

Fixed-Point Data Types

This diagram shows the data types used within the Magnitude FFT subsystem block for fixed-point signals.

The settings for the fixed-point parameters of the FFT block in the diagram above are as follows:

Sine table — Same word length as input
Integer rounding mode — Floor
Saturate on integer overflow — Not selected
Product output — Inherit via internal rule
Accumulator — Inherit via internal rule
Output — Inherit via internal rule

The settings for the fixed-point parameters of the Magnitude Squared block in the diagram are as follows:

Integer rounding mode — Floor
Saturate on integer overflow — Selected
Output — Inherit via internal rule

References

[1] FFTW (https://www.fftw.org)

[2] Frigo, M. and S. G. Johnson, “FFTW: An Adaptive Software Architecture for the FFT,”Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.

[3] Oppenheim, A. V. and R. W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1989.

[4] Orfanidis, S. J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1995.

[5] Proakis, J. and D. Manolakis. Digital Signal Processing. 3rd ed. Englewood Cliffs, NJ: Prentice-Hall, 1996.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Usage notes and limitations:

Generated code relies on the memcpy or memset function (string.h) under certain conditions.
When the following conditions apply, the executable generated from this block relies on prebuilt dynamic library files (.dll files) included with MATLAB:
- You set FFT implementation to FFTW.
- You clear the Inherit FFT length from input dimensions parameter and set FFT length to a value that is not a power of two.
Use the packNGo function to package the code generated from this block and all the relevant files in a compressed zip file. Using this zip file, you can relocate, unpack, and rebuild your project in another development environment where MATLAB is not installed. For more details, see How To Run a Generated Executable Outside MATLAB.
When the FFT length is a power of two, you can generate standalone C and C++ code from this block.

Version History

Introduced before R2006a

Magnitude FFT

Description

Ports

Input

Input — Input
vector | matrix

Output

Output — Magnitude FFT output
vector | matrix

Parameters

Output — Type of output
`Magnitude squared` (default) | `Magnitude`

FFT implementation — FFT implementation
`Auto` (default) | `Radix-2` | `FFTW`

Inherit FFT length from input dimensions — Inherit FFT length from input frame size
`off` (default) | `on`

FFT length — FFT length
`256` (default) | positive integer

Dependency

Wrap input data when FFT length is shorter than input length — Choose to wrap or truncate input
`on` (default) | `off`

Block Characteristics

More About

Fixed-Point Data Types

References

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Functions

Blocks

Topics

Magnitude FFT

Description

Ports

Input

Input — Input vector | matrix

Output

Output — Magnitude FFT output vector | matrix

Parameters

Output — Type of output Magnitude squared (default) | Magnitude

FFT implementation — FFT implementation Auto (default) | Radix-2 | FFTW

Inherit FFT length from input dimensions — Inherit FFT length from input frame size off (default) | on

FFT length — FFT length 256 (default) | positive integer

Dependency

Wrap input data when FFT length is shorter than input length — Choose to wrap or truncate input on (default) | off

Block Characteristics

More About

Fixed-Point Data Types

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

See Also

Functions

Blocks

Topics

Input — Input
vector | matrix

Output — Magnitude FFT output
vector | matrix

Output — Type of output
`Magnitude squared` (default) | `Magnitude`

FFT implementation — FFT implementation
`Auto` (default) | `Radix-2` | `FFTW`

Inherit FFT length from input dimensions — Inherit FFT length from input frame size
`off` (default) | `on`

FFT length — FFT length
`256` (default) | positive integer

Wrap input data when FFT length is shorter than input length — Choose to wrap or truncate input
`on` (default) | `off`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.