mfilt.firsrc

(Removed) Direct-form FIR polyphase sample rate converter

mfilt.firsrc has been removed. Use dsp.FIRRateConverter instead.

Syntax

hm = mfilt.firsrc(l,m,num)

Description

hm = mfilt.firsrc(l,m,num) returns a direct-form FIR polyphase sample rate converter. l specifies the interpolation factor. It must be an integer and when omitted in the calling syntax, it defaults to 2.

m is the decimation factor. It must be an integer. If not specified, m defaults to 1. If l is also not specified, m defaults to 3 and the overall rate change factor is 2/3.

You specify the coefficients of the FIR lowpass filter used for sample rate conversion in num. If omitted, a lowpass Nyquist filter with gain l and cutoff frequency of π/max(l,m) is the default.

Combining an interpolation factor and a decimation factor lets you use mfilt.firsrc to perform fractional interpolation or decimation on an input signal. Using an mfilt.firsrc object applies a rate change factor defined by l/m to the input signal. For proper rate changing to occur, l and m must be relatively prime — meaning the ratio l/m cannot be reduced to a ratio of smaller integers.

When you are doing sample-rate conversion with large values of l or m, such as l or m greater than 20, using the mfilt.firsrc structure is the most effective approach.

Make this filter a fixed-point or single-precision filter by changing the value of the Arithmetic property for the filter hm as follows:

To change to single-precision filtering, enter
```
set(hm,'arithmetic','single');
```
To change to fixed-point filtering, enter
```
set(hm,'arithmetic','fixed');
```

Note

You can use the realizemdl method to create a Simulink^® block of a filter created using mfilt.firsrc.

Input Arguments

The following table describes the input arguments for creating hm.

Input Argument	Description
`l`	Interpolation factor for the filter. `l` specifies the amount to increase the input sampling rate. It must be an integer. When you do not specify a value for `l`, it defaults to 2.
`num`	Vector containing the coefficients of the FIR lowpass filter used for interpolation. When `num` is not provided as an input, `mfilt.firsrc` uses a lowpass Nyquist filter with gain equal to `l` and cutoff frequency equal to π`/max(l,m)` by default. The default length for the Nyquist filter is 24*`max(1,m)`. Therefore, each polyphase filter component has length 24.
`m`	Decimation factor for the filter. `m` specifies the amount to reduce the sampling rate of the input signal. It must be an integer. When you do not specify a value for `m`, it defaults to 1. When `l` is unspecified as well, `m` defaults to 3.

Object Properties

This section describes the properties for both floating-point filters (double-precision and single-precision) and fixed-point filters.

Floating-Point Filter Properties

Every multirate filter object has properties that govern the way it behaves when you use it. Note that many of the properties are also input arguments for creating mfilt.firsrc objects. The next table describes each property for an mfilt.firsrc filter object.

Name	Values	Description
`Arithmetic`	`[Double]`, `single`, `fixed`	Defines the arithmetic the filter uses. Gives you the options `double`, `single`, and `fixed`. In short, this property defines the operation mode for your filter.
`FilterStructure`	Character vector	Reports the type of filter object. You cannot set this property — it is always read only and results from your choice of `mfilt` object. Describes the signal flow for the filter object.
`InputOffset`	Integers	Contains a value derived from the number of input samples and the decimation factor — `InputOffset = mod(length(nx),m)` where `nx` is the number of input samples and `m` is the decimation factor.
`Numerator`	Vector	Vector containing the coefficients of the FIR lowpass filter used for decimation.
`PersistentMemory`	`false`, `true`	Determines whether the filter states get restored to zeros for each filtering operation. The starting values are the values in place when you create the filter if you have not changed the filter since you constructed it. `PersistentMemory` set to `false` returns filter states to the default values after filtering. States that the filter does not change are not affected. Setting this to `true` allows you to modify the `States`, `InputOffset`, and `PolyphaseAccum` properties.
`RateChangeFactors`	Positive integers. [2 3]	Specifies the interpolation and decimation factors [`l m`] (the rate change factors ) for changing the input sample rate by nonintegral amounts.
`States`	`Double`, `single`, matching the filter arithmetic setting.	Contains the filter states before, during, and after filter operations. States act as filter memory between filtering runs or sessions.

Fixed-Point Filter Properties

This table shows the properties associated with the fixed-point implementation of the mfilt.firsrc filter.

Note

The table lists all of the properties that a fixed-point filter can have. Many of the properties listed are dynamic, meaning they exist only in response to the settings of other properties. To view all of the characteristics for a filter at any time, use

info(hm)

where hm is a filter.

For further information about the properties of this filter or any mfilt object, refer to Multirate Filter Properties.

Name	Values	Description
`AccumFracLength`	Any positive or negative integer number of bits. [32]	Specifies the fraction length used to interpret data output by the accumulator. This is a property of FIR filters.
`AccumWordLength`	Any integer number of bits [39]	Sets the word length used to store data in the accumulator.
`Arithmetic`	fixed for fixed-point filters	Setting this to `fixed` allows you to modify other filter properties to customize your fixed-point filter.
`CoeffAutoScale`	[true], false	Specifies whether the filter automatically chooses the proper fraction length to represent filter coefficients without overflowing. Turning this off by setting the value to `false` enables you to change the `NumFracLength` property value to specify the precision used.
`CoeffWordLength`	Any integer number of bits [16]	Specifies the word length to apply to filter coefficients.
`FilterInternals`	[FullPrecision], SpecifyPrecision	Controls whether the filter automatically sets the output word and fraction lengths, product word and fraction lengths, and the accumulator word and fraction lengths to maintain the best precision results during filtering. The default value, `FullPrecision`, sets automatic word and fraction length determination by the filter. `SpecifyPrecision` makes the output and accumulator-related properties available so you can set your own word and fraction lengths for them.
`InputFracLength`	Any positive or negative integer number of bits [15]	Specifies the fraction length the filter uses to interpret input data.
`InputWordLength`	Any integer number of bits [16]	Specifies the word length applied to interpret input data.
`NumFracLength`	Any positive or negative integer number of bits [`14`]	Sets the fraction length used to interpret the numerator coefficients.
`OutputFracLength`	Any positive or negative integer number of bits [32]	Determines how the filter interprets the filter output data. You can change the value of `OutputFracLength` when you set `FilterInternals` to `SpecifyPrecision`.
`OutputWordLength`	Any integer number of bits [39]	Determines the word length used for the output data. You make this property editable by setting `FilterInternals` to `SpecifyPrecision`.
`OverflowMode`	saturate, [wrap]	Sets the mode used to respond to overflow conditions in fixed-point arithmetic. Choose from either `saturate` (limit the output to the largest positive or negative representable value) or `wrap` (set overflowing values to the nearest representable value using modular arithmetic.) The choice you make affects only the accumulator and output arithmetic. Coefficient and input arithmetic always saturates. Finally, products never overflow — they maintain full precision.
`RateChangeFactors`	Positive integers [2 3]	Specifies the interpolation and decimation factors [`l m`] (the rate change factors) for changing the input sample rate by nonintegral amounts.
`RoundMode`	[`convergent`], `ceil`, `fix`, `floor`, `nearest`, `round`	Sets the mode the filter uses to quantize numeric values when the values lie between representable values for the data format (word and fraction lengths). `ceil` - Round toward positive infinity. `convergent` - Round to the closest representable integer. Ties round to the nearest even stored integer. This is the least biased of the methods available in this software. `fix` - Round toward zero. `floor` - Round toward negative infinity. `nearest` - Round toward nearest. Ties round toward positive infinity. `round` - Round toward nearest. Ties round toward negative infinity for negative numbers, and toward positive infinity for positive numbers. The choice you make affects only the accumulator and output arithmetic. Coefficient and input arithmetic always round. Finally, products never overflow — they maintain full precision.
`Signed`	[true], false	Specifies whether the filter uses signed or unsigned fixed-point coefficients. Only coefficients reflect this property setting.
`States`	`fi` object	Contains the filter states before, during, and after filter operations. States act as filter memory between filtering runs or sessions. The states use `fi` objects, with the associated properties from those objects. For details, refer to fixed-point objects in Fixed-Point Designer™ documentation. For information about the ordering of the states, refer to the filter structure section.

Examples

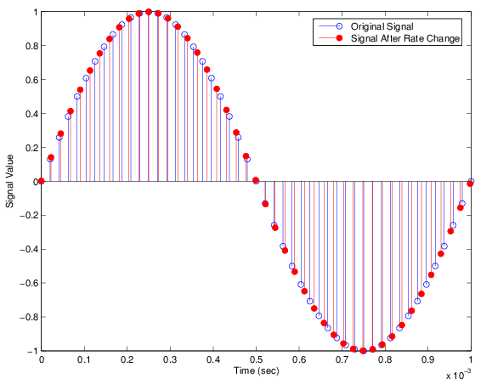
This is an example of a common audio rate change process — changing the sample rate of a high end audio (48 kHz) signal to the compact disc sample rate (44.1 kHz). This conversion requires a rate change factor of 0.91875, or l = 147 and m = 160.

l  = 147; m = 160;            % Interpolation/decimation factors.
hm = mfilt.firsrc(l,m);       % Use the default FIR filter.
fs = 48e3;                    % Original sample freq: 48 kHz.
n = 0:10239;                  % 10240 samples, 0.213 seconds long.
x  = sin(2*pi*1e3/fs*n);      % Original signal, sinusoid at 1 kHz.
y = filter(hm,x);             % 9408 samples, still 0.213 seconds.
stem(n(1:49)/fs,x(1:49))      % Plot original sampled at 48 kHz.
hold on

% Plot fractionally decimated signal (44.1 kHz) in red
stem(n(1:45)/(fs*l/m),y(13:57),'r','filled')
xlabel('Time (sec)');ylabel('Signal Value')

Fractional decimation provides you the flexibility to pick and choose the sample rates you want by carefully selecting l and m, the interpolation and decimation factors, that result in the final fractional decimation. The following figure shows the signal after applying the rate change filter hm to the original signal.

Version History

Introduced in R2011a