Main Content

mfilt.iirinterp

(Removed) IIR interpolator

Compatibility

Note

mfilt.iirinterp has been removed. Use dsp.IIRHalfbandInterpolator instead. For more details, see Version History.

Syntax

hm = mfilt.iirinterp(c1,c2,...)

Description

hm = mfilt.iirinterp(c1,c2,...) constructs an IIR interpolator filter given the coefficients specified in the cell arrays C1, C2, etc.

The IIR interpolator is a polyphase IIR filter where each phase is a cascade allpass IIR filter.

Each cell array ci contains a set of vectors representing a cascade of allpass sections. Each element in one cell array is one section. For more information about the contents of each cell array, refer to dfilt.cascadeallpass. The contents of the cell arrays are the same for both filter constructors and mfilt.iirdecim interprets them same way as mfilt.cascadeallpass.

The following exception applies to interpreting the contents of a cell array—if one of the cell arrays ci contains only one vector, and that vector comprises a series of 0s and a unique element equal to 1, that cell array represents a dfilt.delay section with latency equal to the number of zeros, rather than a dfilt.cascadeallpass section. This exception case occurs with quasi-linear phase IIR interpolators.

Although the first example shows how to construct an IIR interpolator explicitly, one usually constructs an IIR interpolator filter as a result of designing an interpolator, as shown in the subsequent examples.

Examples

When the coefficients are known, you can construct the IIR interpolator directly using mfilt.iirinterp. In the following example, a cascaded polyphase IIR interpolator filter is constructed using 2 phases for each of three stages. The coefficients are given below:

Phase1Sect1=0.0603;Phase1Sect2=0.4126; Phase1Sect3=0.7727; 
Phase2Sect1=0.2160; Phase2Sect2=0.6044; Phase2Sect3=0.9239;

Next the filter is implemented by passing the above coefficients to mfilt.iirinterp as cell arrays, where each cell array represents a different phase.

Hm = mfilt.iirinterp({Phase1Sect1,Phase1Sect2,Phase1Sect3},...
{Phase2Sect1,Phase2Sect2,Phase2Sect3})
 
Hm =
 
        FilterStructure: 'IIR Polyphase Interpolator'
              Polyphase: Phase1: Section1: 0.0603
                               Section2: 0.4126
                               Section3: 0.7727
                         Phase2: Section1: 0.216 
                               Section2: 0.6044
                               Section3: 0.9239
    InterpolationFactor: 2
       PersistentMemory: false

Also refer to the “Quasi-Linear Phase Halfband and Dyadic Halfband Designs” section of IIR Halfband Stages in Multistage Filter Design.

When the coefficients are not known, use the approach given by the following set of examples. Start by designing an elliptic halfband interpolator with a interpolation factor of 2.

tw = 100;  % Transition width of filter.
ast = 80;   % Stopband attenuation of filter.
fs = 2000; % Sampling frequency of filter.
l  = 2;    % Interpolation factor.
d = fdesign.interpolator(l,'halfband','tw,ast',tw,ast,fs);

Specification object d stores the interpolator design specifics. With the details in d, design the filter, returning hm, an mfilt.iirinterp object. Use hm to realize the filter if you have Simulink® installed.

hm = design(d,'ellip','filterstructure','iirinterp'); 
% Note that realizemdl requires Simulink
realizemdl(hm)     % Build model of the filter.

Designing a linear phase halfband interpolator follows the same pattern.

tw = 100;  % Transition width of filter. 
ast= 60;   % Stopband attenuation of filter.
fs = 2000; % Sampling frequency of filter.
l = 2;     % Interpolation factor.
d = fdesign.interpolator(l,'halfband','tw,ast',tw,ast,fs);

fdesign.interpolator returns a specification object that stores the design features for an interpolator.

Now perform the actual design that results in an mfilt.iirinterp filter, hm.

hm = design(d,'iirlinphase','filterstructure','iirinterp');
% Note that realizemdl requires Simulink
realizemdl(hm)     % Build model of the filter.

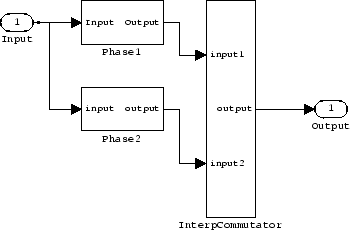
The toolbox creates a Simulink model for hm, shown here. Phase1, Phase2, and InterpCommutator are all subsystem blocks.

Version History

Introduced in R2011a

collapse all

R2022a: mfilt.iirinterp has been removed

mfilt.iirinterp has been removed. Use dsp.IIRHalfbandInterpolator instead.

Update Code

This table shows how the mfilt.iirinterp object is typically used and explains how to update existing code to use the dsp.IIRHalfbandInterpolator object.

Discouraged UsageRecommended Replacement

Create an mfilt.iiriinterp object using the fdesign.interpolator specification object followed by the design function.

Note that the fdesign.interpolator object accepts the sample rate of the filter, while the dsp.IIRHalfbandInterpolator object accepts the sample rate of the input.

The sample rate of the filter (output) is 2000 Hz.

% Sample rate of filter
FsFilter = 2000;     
% Transition width of the filter (wrt filter sample rate)
tw = 100;  
% Stopband attenuation of filter 
ast = 80;

Create an mfilt.iirinterp object using these specifications.

d = fdesign.interpolator(2,'halfband','tw,ast',tw,ast,FsFilter);
Hm = design(d,'ellip','filterstructure','iirinterp')

Create sinusoidal data and pass the data through the object.

% Input sample rate
FsIn = FsFilter/2; 
% 5120 samples, 0.232 second long signal            
n = (0:5119)';     
% Original signal, sinusoid at 1 kHz             
x  = sin(2*pi*1e3/FsIn*n);
% 10240 samples, still 0.232 seconds     
y_mfilt = filter(Hm,x);

Initialize the dsp.IIRHalfbandInterpolator object. This object accepts the sample rate of the input signal.

% Sample rate of filter
FsFilter = 2000;    
% Input sample rate
FsIn = FsFilter/2;  
% Transition width of the filter
tw = 100;  
% Stopband attenuation of filter 
ast = 80;

Create a dsp.IIRHalfbandInterpolator object using these specifications.

iirI = dsp.IIRHalfbandInterpolator(SampleRate=FsIn,...
TransitionWidth=tw,...
StopbandAttenuation=ast);

Create sinusoidal data and pass the data through the object.

% 5120 samples, 0.232 second long signal            
n = (0:5119)';     
% Original signal, sinusoid at 1 kHz             
x  = sin(2*pi*1e3/FsIn*n);
% 10240 samples, still 0.232 seconds     
y = iirI(x);

See Also