simsmooth

Bayesian nonlinear non-Gaussian state-space model simulation smoother

Since R2024a

Syntax

X = simsmooth(Mdl,Y,params)

X = simsmooth(Mdl,Y,params,Name=Value)

[X,OutputFilter,x0] = simsmooth(___)

Description

simsmooth provides random paths of states drawn from the posterior smoothed state distribution, which is the distribution of the states conditioned on model parameters Θ and the full-sample response data, of a Bayesian nonlinear non-Gaussian state-space model (bnlssm).

To draw state paths from the posterior smoothed state distribution, simsmooth uses the nonlinear forward-filtering, backward-sampling method (FFBS), in which it implements sequential Monte Carlo (SMC) to perform forward filtering, and then it resamples and reweights particles (weighted random samples) generated by SMC to perform backward sampling.

X = simsmooth(Mdl,Y,params) returns a randomly drawn path of states, simulated from the posterior smoothed state distribution, by applying the simulation smoother to the input Bayesian nonlinear non-Gaussian state-space model and responses data. simsmooth uses FFBS to obtain the random path from the posterior smoothed state distribution. simsmooth evaluates the parameter map Mdl.ParamMap by using the input vector of parameter values.

example

X = simsmooth(Mdl,Y,params,Name=Value) specifies additional options using one or more name-value arguments. For example, simsmooth(Mdl,Y,params,NumPaths=1e4,Resample="residual") specifies generating 1e4 random paths and to resample residuals.

example

[X,OutputFilter,x0] = simsmooth(___) additionally returns the following quantities using any of the input-argument combinations in the previous syntaxes:

OutputFilter — SMC forward filtering results by sampling time containing the following quantities:
- Approximate loglikelihood values associated with the input data, input parameters, particles, and posterior state filtering distribution
- Filter estimate of state-distribution means
- Filter estimate of state-distribution covariance
- State particles and corresponding weights that approximate the filtering distribution
- Effective sample size
- Flags indicating which data the software used to filter
- Flags indicating resampling
x0 — Simulation-smoothed initial state, computed only when you request the this output

example

Examples

collapse all

Draw Path from Posterior Smoothed State Distribution

Open Live Script

This example draws a random path from the approximate posterior smoothed state distribution of the Bayesian nonlinear state-space model in equation. The state-space model contains two independent, stationary, autoregressive states each with a model constant. The observations are a nonlinear function of the states with Gaussian noise. The prior distribution of the parameters is flat. Symbolically, the system of equations is

$[\begin{array}{cccccccccccccccccccc} x_{1, t} \\ x_{2, t} \\ x_{3, t} \\ x_{4, t} \end{array}] = [\begin{array}{cccccccccccccccccccc} θ_{1} & θ_{2} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & θ_{3} & θ_{4} \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \\ x_{3, t - 1} \\ x_{4, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} θ_{5} & 0 \\ 0 & 0 \\ 0 & θ_{6} \\ 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{1, t} \\ u_{3, t} \end{array}]$

$y_{t} = \log (\exp (x_{1, t} - μ_{1}) + \exp (x_{3, t} - μ_{3})) + θ_{7} ε_{t} .$

$μ_{1}$ and $μ_{3}$ are the unconditional means of the corresponding states. The initial distribution moments of each state are their unconditional mean and covariance.

Create a Bayesian nonlinear state-space model characterized by the system. The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series $ε_{t}$ is additive, linear, and Gaussian. The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function and the prior distribution of the parameters. You can use the functions only within this script.

Mdl = bnlssm(@paramMap,@priorDistribution)

Mdl = 
  bnlssm with properties:

             ParamMap: @paramMap
    ParamDistribution: @priorDistribution
      ObservationForm: "equation"
           Multipoint: [1×0 string]

Mdl is a bnlssm model specifying the state-space model structure and prior distribution of the state-space model parameters. Because Mdl contains unknown values, it serves as a template for posterior analysis with observations.

Simulate a series of 100 observations from the following stationary 2-D VAR process.

$\begin{array}{l} x_{1, t} = 1 + 0.9 x_{1, t - 1} + 0.3 u_{1, t} \\ x_{3, t} = - 1 - 0.75 x_{3, t - 1} + 0.2 u_{3, t}, \end{array}$

where the disturbance series $u_{j, t}$ are standard Gaussian random variables.

rng(1,"twister")    % For reproducibility
T = 100;
thetatrue = [0.9; 1; -0.75; -1; 0.3; 0.2; 0.1];
MdlSim = varm(AR={diag(thetatrue([1 3]))},Covariance=diag(thetatrue(5:6).^2), ...
    Constant=thetatrue([2 4]));
XSim = simulate(MdlSim,T);

Compose simulated observations using the following equation.

$y_{t} = \log (\exp (x_{1, t} - {x_{}^{‾}}_{1}) + \exp (x_{3, t} - {x_{}^{‾}}_{3})) + 0.1 ε_{t},$

where the innovation series $ε_{t}$ is a standard Gaussian random variable.

ysim = log(sum(exp(XSim - mean(XSim)),2)) + thetatrue(7)*randn(T,1);

To draw from the approximate posterior smoothed state distribution, the simsmooth function requires response data and a model with known state-space model parameters. Choose a random set with the following constraints:

$θ_{1}$ and $θ_{3}$ are within the unit circle. Use $U (- 1, 1)$ to generate values.
$θ_{2}$ and $θ_{4}$ are real numbers. Use the $N (0, 3^{2})$ distribution to generate values.
$θ_{5}$ , $θ_{6}$ , and $θ_{7}$ are positive real numbers. Use the $χ_{1}^{2}$ distribution to generate values.

theta13 = (-1+(1-(-1)).*rand(2,1));
theta24 = 3*randn(2,1);
theta567 = chi2rnd(1,3,1);
theta = [theta13(1); theta24(1); theta13(2); theta24(2); theta567];

Draw a random path from the approximate smoothed state posterior distribution by passing the Bayesian nonlinear model, simulated data, and parameter values to simsmooth.

SmoothX = simsmooth(Mdl,ysim,theta);
size(SmoothX)

ans = 1×2

   100     4

SmoothX is a 100-by-4 matrix containing one path drawn from the approximate posterior smoothed state distribution, with rows corresponding to periods in the sample and columns corresponding to the state variables. The simsmooth function uses the FFBS method (SMC and a bootstrap to resample particles and weights) to obtain draws from the posterior smoothed state distribution.

Draw another path, but specify $Θ$ used to simulate the data.

SmoothXSim = simsmooth(Mdl,ysim,thetatrue);

Plot the two paths with the true state values.

figure
tiledlayout(2,1)
nexttile
plot([SmoothX(:,1) SmoothXSim(:,1) XSim(:,1)])
title("x_{t,1}")
legend("Smoothed State, random \theta","Smoothed State, true \theta","XSim")
nexttile
plot([SmoothX(:,3) SmoothXSim(:,3) XSim(:,2)])
title("x_{t,3}")
legend("Smoothed State, random \theta","Smoothed State, true \theta","XSim")

$Figure contains 2 axes objects. Axes object 1 with title x indexOf t, 1 baseline contains 3 objects of type line. These objects represent Smoothed State, random \theta, Smoothed State, true \theta, XSim. Axes object 2 with title x indexOf t, 3 baseline contains 3 objects of type line. These objects represent Smoothed State, random \theta, Smoothed State, true \theta, XSim.$

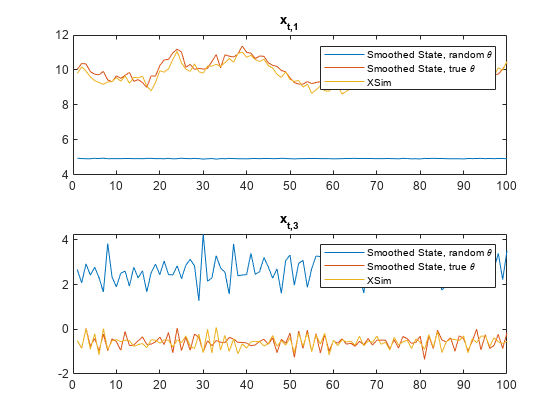
The paths using the true value of $Θ$ and the simulated state paths are close. The paths generated from the random value of $Θ$ is far from the simulated state paths.

Local Functions

These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = @(x)blkdiag([theta(1) theta(2); 0 1],[theta(3) theta(4); 0 1])*x; 
    B = [theta(5) 0; 0 0; 0 theta(6); 0 0];
    C = @(x)log(exp(x(1)-theta(2)/(1-theta(1))) + ...
        exp(x(3)-theta(4)/(1-theta(3))));
    D = theta(7);
    Mean0 = [theta(2)/(1-theta(1)); 1; theta(4)/(1-theta(3)); 1];         
    Cov0 = diag([theta(5)^2/(1-theta(1)^2) 0 theta(6)^2/(1-theta(3)^2) 0]);          
    StateType = [0; 1; 0; 1];     % Stationary state and constant 1 processes
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta([1 3])) >= 1); (theta(5:7) <= 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Estimate Model Parameters Using Gibbs Sampler

Open Live Script

This example shows how to draw from the posterior distribution of smoothed states and model parameters by using a Gibbs sampler. Consider this nonlinear state-space model

$\begin{array}{l} x_{t} = ϕ x_{t - 1} + σ u_{t} \\ y_{t} \sim P o i s s o n (λ e^{x_{t}}), \end{array}$

where the parameters in $Θ = {ϕ, σ, λ}$ have the following priors:

$ϕ \sim N_{(- 1, 1)} (m_{0}, v_{0}^{2})$ , that is, a truncated normal distribution with $ϕ \in [- 1, 1]$ .
$σ^{2} \sim IG (a_{0}, b_{0})$ , that is, an inverse gamma distribution with shape $a_{0}$ and scale $b_{0}$ .
$λ \sim Gamma (α_{0}, β_{0})$ , that is, a gamma distribution with shape $α_{0}$ and scale $β_{0}$ .

Simulate Series

Consider this data-generating process (DGP).

$\begin{array}{l} x_{t} = 0.7 x_{t - 1} + \sqrt{0.2} u_{t} \\ y_{t} \sim P o i s s o n (3 e^{x_{t}}), \end{array}$

where the series $u_{t}$ is a standard Gaussian series of random variables.

Simulate a series of 200 observations from the process.

rng(500,"twister")    % For reproducibility
T = 200;
thetaDGP = [0.7; 0.2; 3];

numparams = numel(thetaDGP);

MdlXSim = arima(AR=thetaDGP(1),Variance=thetaDGP(2), ...
    Constant=0);
xsim = simulate(MdlXSim,T);
y = random("poisson",thetaDGP(3)*exp(xsim));

figure
plot(y)

Figure contains an axes object. The axes object contains an object of type line.

Create Bayesian Nonlinear Model

The Local Functions section contains the functions paramMap and logPrior required to specify the Bayesian nonlinear state-space model. The paramMap function specifies the state-space model structure and initial state moments. The priorDistribution function returns the log of the joint prior distribution of the state-space model parameters. You can use the functions only within this script.

Create a Bayesian nonlinear state-space model for the DGP. Indicate that the state-space model observation equation is expressed as a distribution. To speed up computations, the arguments A and LogY of the paramMap function are written to enable simultaneous evaluation of the transition and observation densities of multiple particles. Specify this characteristic by using the Multipoint name-value argument.

Mdl = bnlssm(@paramMap,@priorDistribution,ObservationForm="distribution", ...
    Multipoint=["A" "LogY"]);

Perform Gibbs Sampling

A Gibbs sampler is an Markov chain Monte Carlo method for drawing a sample from the joint posterior distribution of parameters. It successively draws from the full conditional distributions of the states and model parameters, one at a time; results of previous draws are substituted, which enables the Markov chains to explore the parameter space.

The full conditional distribution of the states is the posterior of the smoothed state distribution, which simsmooth computes. The remaining full conditionals are:

$π (ϕ | x, y, σ^{2}, λ) \sim N_{(- 1, 1)} (m_{ϕ}, v_{ϕ}^{2})$ , where $m_{ϕ} = \frac{v_{0}^{2} \sum_{t = 2}^{T} x_{t} x_{t - 1} + σ^{2} m_{0}}{v_{0}^{2} \sum_{t = 2}^{T} x_{t - 1}^{2} + σ^{2}}$ and $v_{ϕ}^{2} = \frac{σ^{2} v_{0}^{2}}{v_{0}^{2} \sum_{t = 2}^{T} x_{t - 1}^{2} + σ^{2}}$ .
$π (σ^{2} | x, y, ϕ, λ) \sim IG (a_{σ^{2}}, b_{σ^{2}})$ , where $a_{σ^{2}} = a_{0} + \frac{T - 1}{2}$ and $b_{σ^{2}} = \frac{b_{0}}{{1 + 0.5 b}_{0} \sum_{t = 2}^{T} {(x_{t} {- ϕ x}_{t - 1})}^{2}}$ .
$π (λ | x, y, ϕ, σ^{2}) \sim Gamma (α_{λ}, β_{λ})$ , where $α_{λ} = α_{0} + \sum_{t = 1}^{T} y_{t}$ and $β_{λ} = \frac{β_{0}}{1 + β_{0} \sum_{t = 1}^{T} e^{x_{t}}}$ .

You can view the joint posterior distribution $π (ϕ, σ^{2} | x, y, λ)$ as the semiconjugate Bayesian linear regression model $z_{t} = {ϕ w}_{t} + v_{t}$ , where the response series $z_{t} = {x_{2}, . . ., x_{T}}$ , predictor series $w_{t} = {x_{1}, . . ., x_{T - 1}}$ , and the error series $v_{t} \sim N (0, σ^{2})$ . If you view the problem this way, you can speed up sampler. During sampling, you can reject any $ϕ$ draws outside its support.

The Local Functions section contains the following functions:

phiFC — Draws from $π (ϕ | x, y, σ^{2}, λ)$
sigma2FC — Draws from $π (σ^{2} | x, y, ϕ, λ)$
lambdaFC — Draws from $π (λ | x, y, ϕ, σ^{2})$

Conduct the Gibbs sampler. Draw a sample of 2000 from the full conditional distributions. Draw 1500 particles for each call of simsmooth. Perform rejection sampling at a maximum of 50 iterations. This example chooses the initial conditions arbitrarily.

nGibbs = 2000;
Gibbs = zeros(T+numparams,nGibbs); % Preallocate for state and parameter draws
numparticles = 1500;
maxiterations = 50;

% Initial values
% theta
theta0 = [0.5; 0.1; 2]; 

% pi(phi,sigma2) hyperparameters
m0 = 0;                 
v02 = 1;
a0 = 1;
b0 = 1;
MdlBLM = semiconjugateblm(1,Intercept=0,Mu=m0,V=v02, ...
    A=a0,B=b0);

% lambda hyperparameters
alpha0 = 3;
beta0 = 1;

hyperparams = [m0 v02 a0 b0 alpha0 beta0];

% Prepare wait bar dialog box
wb = waitbar(0,"1",Name="Running Gibbs Sampler ...", ...
    CreateCancelBtn="setappdata(gcbf,Canceling=true)");
setappdata(wb,Canceling=false);

% Gibbs sampler
theta = theta0;
for j = 1:nGibbs
    % Press Cancel in the dialog to break.
    if getappdata(wb,"Canceling")
        fprintf("Gibbs sampler canceled")
        break
    end
    waitbar(j/nGibbs,wb,sprintf("Draw %d of %d",j,nGibbs));
    Gibbs(1:T,j) = simsmooth(Mdl,y,theta,NumParticles=numparticles, ...
        MaxIterations=maxiterations);
    [Gibbs(T+1,j),Gibbs(T+2,j)] = blmFC(Gibbs(1:T,j),MdlBLM,theta);
    Gibbs(T+3,j) = lambdaFC(Gibbs(1:T,j),y,hyperparams);
    theta = Gibbs(T+(1:3),j);
end
delete(wb)

Describe $π (Θ | y)$

To reduce the influence of initial conditions on the sample, remove the first 50 draws from the Gibbs sample. To reduce the influence of serial correlation in the sample, thin the sample by keeping every fourth draw.

burnin = 50;
thin = 4;
pphi = Gibbs(T+1,burnin:thin:end);
psigma2 = Gibbs(T+2,burnin:thin:end);
plambda = Gibbs(T+3,burnin:thin:end);

Plot trace plots of the Gibbs sampler.

figure
h = tiledlayout(3,1);
nexttile
plot(pphi)
title("\pi(\phi|y)")
nexttile
plot(psigma2)
title("\pi(\sigma^2|y)")
nexttile
plot(plambda)
title("\pi(\lambda|y)")
title(h,"Trace Plots")

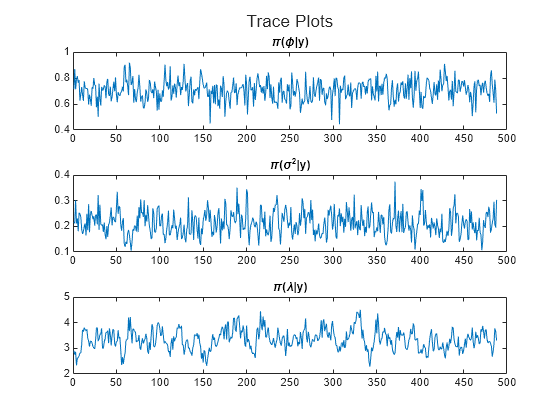
Figure contains 3 axes objects. Axes object 1 with title pi ( phi |y) contains an object of type line. Axes object 2 with title pi ( sigma Squared baseline |y) contains an object of type line. Axes object 3 with title pi ( lambda |y) contains an object of type line.

The trace plots show that the Markov chains are mixing adequately.

Summarize the posterior distributions by computing sample medians and 95% percentile intervals of the processed posterior draws. Plot histograms of the posterior distributions of the model parameters.

mphi = median(pphi);
ciphi = quantile(pphi,[0.025 0.975]);
msigma2 = median(psigma2);
cisigma2 = quantile(psigma2,[0.025 0.975]);
mlambda = median(plambda);
cilambda = quantile(plambda,[0.025 0.975]);

figure
h = tiledlayout(3,1);
nexttile
histogram(pphi)
title(sprintf("\\pi(\\phi|y), median=%.3f, ci=(%.3f, %.3f)",mphi,ciphi))
nexttile
histogram(psigma2)
title(sprintf("\\pi(\\sigma^2|y), median=%.3f, ci=(%.3f, %.3f)",msigma2,cisigma2))
nexttile
histogram(plambda)
title(sprintf("\\pi(\\lambda|y), median=%.3f, ci=(%.3f, %.3f)",mlambda,cilambda))
title(h,"Posterior Histograms")

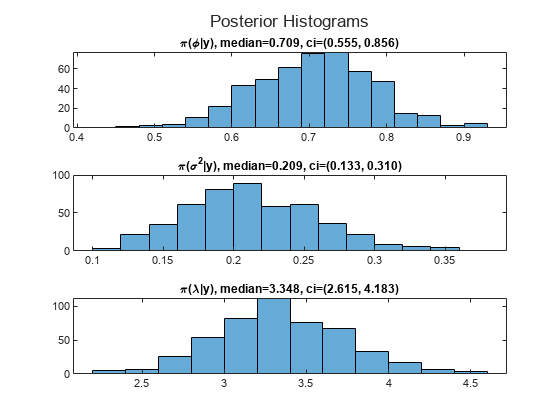
The posterior medians are close to their DGP counterparts.

Local Functions

These functions specify the state-space model parameter mappings, in distribution form, the log prior distribution of the parameters, and random draws from full conditional distribution of each parameter.

function [A,B,LogY,Mean0,Cov0,StateType] = paramMap(theta)
    A = theta(1); 
    B = sqrt(theta(2));
    LogY = @(y,x)y.*x - exp(x).*theta(3);
    Mean0 = 0;
    Cov0 = 2;
    StateType = 0;     % Stationary state process
end

function logprior = priorDistribution(theta,hyperparams)
    % Prior of phi
    m0 = hyperparams(1);
    v20 = hyperparams(2);
    pphi = makedist("normal",mu=m0,sigma=sqrt(v20));
    pphi = truncate(pphi,-1,1);
    lpphi = log(pdf(pphi,theta(1)));

    % Prior of sigma2
    a0 = hyperparams(3);
    b0 = hyperparams(4);
    lpsigma2 = -a0*log(b0) - log(gamma(a0)) + (-a0-1)*log(theta(2)) - ...
        1./(b0*theta(2));

    % Prior of lambda
    alpha0 = hyperparams(5);
    beta0 = hyperparams(6);
    plambda = makedist("gamma",alpha0,beta0);
    lplambda = log(pdf(plambda,theta(3))); 

    logprior = lpphi + lpsigma2 + lplambda;
end

function [phi,sigma2] = blmFC(x,mdl,theta)
    % Reject sampled phi when it is outside the unit circle
    while true
        phi = simulate(mdl,x(1:end-1),x(2:end),Sigma2=theta(2));
        if abs(phi) < 1
            break
        end
    end
    [~,sigma2] = simulate(mdl,x(1:(end-1)),x(2:end),Beta=theta(1));
end

function [lambda,alpha,beta] = lambdaFC(x,y,hyperparams)
   alpha0 = hyperparams(5);
   beta0 = hyperparams(6);
   alpha = sum(y) + alpha0;
   beta = beta0./(beta0*sum(exp(x))+1);
   lambda = gamrnd(alpha,beta,1);
end

Monitor Underlying Sampling Procedures

Open Live Script

simsmooth runs SMC to forward filter the state-space model, which includes resampling particles. To assess the quality of the sample, including whether any posterior filtered state distribution is close to degenerate, you can monitor these algorithms by returning the third output of smooth.

Consider this nonlinear state-space model.

$[\begin{array}{cccccccccccccccccccc} x_{t, 1} \\ x_{t, 2} \\ x_{t, 3} \\ x_{t, 4} \end{array}] = [\begin{array}{cccccccccccccccccccc} θ_{1} & θ_{2} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & θ_{3} & θ_{4} \\ 0 & 0 & 0 & 1 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{t - 1, 1} \\ x_{t - 1, 2} \\ x_{t - 1, 3} \\ x_{t - 1, 4} \end{array}] + [\begin{array}{cccccccccccccccccccc} θ_{5} & 0 \\ 0 & 0 \\ 0 & θ_{6} \\ 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} u_{t, 1} \\ u_{t, 3} \end{array}]$

$y_{t} = \log (\exp (x_{t, 1} - μ_{1}) + \exp (x_{t, 3} - μ_{3})) + θ_{7} ε_{t} .$

$μ_{1}$ and $μ_{3}$ are the unconditional means of the corresponding states. The initial distribution moments of each state are their unconditional mean and covariance.

Simulate a series of 100 observations from the following stationary 2-D VAR process.

$\begin{array}{l} x_{t, 1} = 1 + 0.9 x_{t - 1, 1} + 0.3 u_{t, 1} \\ x_{t, 3} = - 1 + - 0.75 x_{t - 1, 3} + 0.2 u_{t, 3} \\ y_{t} = \log (\exp (x_{t, 1} - {x_{}^{‾}}_{1}) + \exp (x_{t, 3} - {x_{}^{‾}}_{3})) + 0.1 ε_{t}, \end{array}$

where the disturbance series $u_{t, j}$ and $ε_{t}$ are standard Gaussian random variables.

rng(100,"twister")    % For reproducibility
T = 100;
thetatrue = [0.9; 1; -0.75; -1; 0.3; 0.2; 0.1];
MdlSim = varm(AR={diag(thetatrue([1 3]))},Covariance=diag(thetatrue(5:6).^2), ...
    Constant=thetatrue([2 4]));
XSim = simulate(MdlSim,T);
y = log(sum(exp(XSim - mean(XSim)),2)) + thetatrue(7)*randn(T,1);

Create a Bayesian nonlinear state-space model. The Local Functions section contains the required functions specifying the Bayesian nonlinear state-space model structure and joint prior distribution.

Mdl = bnlssm(@paramMap,@priorDistribution);

Approximate the posterior smoothed state distribution of the state-space model. As in the Draw Path from Posterior Smoothed State Distribution example, choose a random set of initial parameter values. Specify the resampling residuals for the SMC. Return the forward-filtering results and the approximate initial smoothed state $x_{0}$ .

theta13 = (-1+(1-(-1)).*rand(2,1));
theta24 = 3*randn(2,1);
theta567 = chi2rnd(1,3,1);
theta = [theta13(1); theta24(1); theta13(2); theta24(2); theta567];

[~,OutputFilter,x0] = simsmooth(Mdl,y,theta,Resample="residual");

Output is a 100-by-1 structure array containing several fields, one set of fields for each observation, including:

FilteredStatesCov — Approximate posterior filtered state distribution covariance for the states at each sampling time
DataUsed — Whether the forward-filtering algorithm used an observation for posterior estimation
Resample — Whether the forward-filtering algorithm resampled the particles associated with an observation

Plot the determinant of the approximate posterior filtered state covariance matrices for states that are not constant.

filteredstatecov = cellfun(@(x)det(x([1 3],[1 3])),{OutputFilter.FilteredStatesCov});

figure
plot(filteredstatecov)
title("Approx. Post. Filtered State Covariances")

Figure contains an axes object. The axes object with title Approx. Post. Filtered State Covariances contains an object of type line.

Any covariance determinant that is close to 0 indicates a close-to-degenerate distribution. No covariance determinants in the analysis are close to 0.

Determine whether the forward-filtering algorithm omitted any observations from posterior estimation.

anyObsOmitted = sum([OutputFilter.DataUsed]) ~= T

anyObsOmitted = logical
   0

anyObsOmitted = 0 indicates that the algorithm used all observations.

Determine whether filter resampled any particles associated with observations.

whichResampled = numel(find([OutputFilter.Resampled] == true))

whichResampled = 
75

The forward-filtering algorithm resampled particles associated with observations the 75 observations listed in whichResampled.

Local Functions

These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.

function [A,B,C,D,Mean0,Cov0,StateType] = paramMap(theta)
    A = @(x)blkdiag([theta(1) theta(2); 0 1],[theta(3) theta(4); 0 1])*x; 
    B = [theta(5) 0; 0 0; 0 theta(6); 0 0];
    C = @(x)log(exp(x(1)-theta(2)/(1-theta(1))) + ...
        exp(x(3)-theta(4)/(1-theta(3))));
    D = theta(7);
    Mean0 = [theta(2)/(1-theta(1)); 1; theta(4)/(1-theta(3)); 1];         
    Cov0 = diag([theta(5)^2/(1-theta(1)^2) 0 theta(6)^2/(1-theta(3)^2) 0]);          
    StateType = [0; 1; 0; 1];     % Stationary state and constant 1 processes
end

function logprior = priorDistribution(theta)
    paramconstraints = [(abs(theta([1 3])) >= 1) (theta(5:7) <= 0)];
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Compare SMC Proposal Methods

Open Live Script

This example compares the performance of several SMC proposal particle resampling methods for obtaining random paths from the posterior smoothed state distribution of a quasi-nonnegative constrained state space model, which models nonnegative state quantities such as interest rates and prices:

$\begin{array}{l} x_{t} = \max (0, a_{0} + a_{1} x_{t - 1}) + b u_{t} \\ y_{t} = x_{t} + d ε_{t} . \end{array}$

$u_{t}$ and $ε_{t}$ are iid standard Gaussian random variables.

Generate Artificial Data

Consider the following data-generating process (DGP)

$\begin{array}{l} x_{t} = \max (0, 0.1 + 0.95 x_{t - 1}) + u_{t} \\ y_{t} = x_{t} + 0.5 ε_{t} . \end{array}$

Generate a random series of 200 observations from the DGP.

a0 = 0.1;
a1 = 0.95;
b = 1;
d = 0.5;
theta = [a0; a1; b; d];
T = 50;

% Preallocate variables
x = zeros(T,1);
y = zeros(T,1);

rng(0,"twister") % For reproducibility
u = randn(T,1);
e = randn(T,1);

for t = 2:T
    x(t) = max(0,a0 + a1*x(t-1)) + b*u(t);
    y(t) = x(t) + d*e(t);               
end

Create Bayesian Nonlinear State-Space Model

The Local Functions section contains two functions required to specify the Bayesian nonlinear state-space model: the state-space model parameter mapping function paramMap and the prior distribution of the parameters priorDistribution. You can use the functions only within this script.

The paramMap function has these qualities:

Functions can simultaneously evaluate the state equation for multiple values of A. Therefore, you can speed up calculations by specifying the Multipoint="A" option.
The observation equation is in equation form, that is, the function composing the states is nonlinear and the innovation series $ε_{t}$ is additive, linear, and Gaussian.

The priorDistribution function specifies a flat prior, which has a density that is proportional to 1 everywhere in the parameter space; it constrains the error standard deviations to be positive.

Create a Bayesian nonlinear state-space model characterized by the system.

Mdl = bnlssm(@paramMap,@priorDistribution,Multipoint="A");

Draw Smoothed State Paths from Posterior Using Each Proposal Sampler Method

Obtain a random path from the posterior smoothed state distribution using the joint posterior distribution of the parameters, at a randomly drawn set of values in [0,1], using the bootstrap, optimal, and one-pass unscented particle resampling methods. Specify drawing 5000 particles for SMC.

numParticles = 5000;
smcMethod = ["bootstrap" "optimal" "unscented"];
params = rand(4,1);
for j = 3:-1:1 % Set last element first to preallocate entire cell vector
    xSS{j} = simsmooth(Mdl,y,params,NewSamples=smcMethod(j),NumParticles=numParticles,NumPaths=100);
    XSSStats{j} = quantile(squeeze(xSS{j}),[0.025 0.5 0.975],2);
end

Compare the smoothed state paths from each method with the true values.

figure
tiledlayout(3,1)
for j = 1:3
    nexttile
    h1 = plot([x XSSStats{j}(:,2)]);
    hold on
    h2 = plot(XSSStats{j}(:,[1 3]),"g--");
    hold off
    title("SMC Method: " + upper(smcMethod(j)))
end
legend([h1; h2(1)],["True" "Median" "95% Interval"])

Figure contains 3 axes objects. Axes object 1 with title SMC Method: BOOTSTRAP contains 4 objects of type line. Axes object 2 with title SMC Method: OPTIMAL contains 4 objects of type line. Axes object 3 with title SMC Method: UNSCENTED contains 4 objects of type line. These objects represent True, Median, 95% Interval.

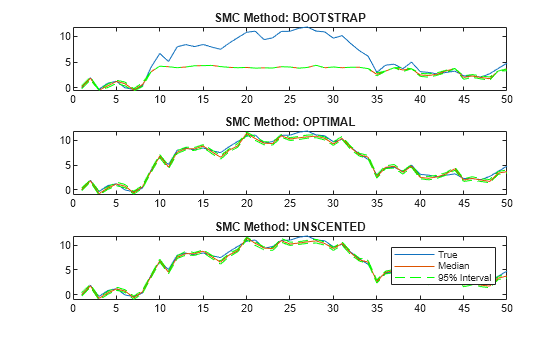
The figure shows that, in this case, the optimal and one-pass unscented methods yield simulated smoothed state estimates closer to the true values than the bootstrap method. For the bootstrap method, simulated smoothed state estimates in periods 10 through 35 level off around 5, while the true values jump as high as 10. The reason is the bootstrap filter updates particles solely by the transition equation—observations do not inform how particles are updated unlike the optimal and unscented methods.

Regardless of method, simsmooth weighs particles by the observation densities. In this example, the observation equation is $y_{t} = x_{t} + 0.17 ε_{t}$ . For the bootstrap filter, the normally distributed observation innovation, with small loading 0.17, cannot accommodate large jumps, such as from 5 to 10. Consequently, the weights are degenerate: the largest particle takes all the weight, and simsmooth discards the remaining particles during resampling because they have zero weight. The simulated smoothed state estimates level off until period 35 when the observations fall below 5.

Local Functions

These functions specify the state-space model parameter mappings, in equation form, and log prior distribution of the parameters.

function [A,B,C,D,mean0,Cov0] = paramMap(params)
    a0 = params(1);
    a1 = params(2);
    b = params(3);
    d = params(4);
    A = @(x) max(0,a0+a1.*x);
    B = b;
    C = 1;
    D = d;
    mean0 = 0;
    Cov0 = 1;
end

function logprior = priorDistribution(theta)
    paramconstraints = theta(3:4) <= 0; % b and d are greater than 0
    if(sum(paramconstraints))
        logprior = -Inf;
    else 
        logprior = 0;   % Prior density is proportional to 1 for all values
                        % in the parameter space.
    end
end

Input Arguments

collapse all

`Mdl` — Bayesian nonlinear state-space model
`bnlssm` model object

Bayesian nonlinear state-space model, specified as a bnlssm model object created by the bnlssm function.

The function handles of the properties Mdl.ParamDistribution and Mdl.ParamMap determine the prior and the data likelihood, respectively. simsmooth evaluates Mdl.ParamMap at the input params.

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

Observed response data, specified as a numeric matrix or a cell vector of numeric vectors.

If Mdl is time invariant with respect to the observation equation, Y is a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. T is the sample size and n is the number of observations per period. The last row of Y contains the latest observations.
If Mdl is time varying with respect to the observation equation, Y is a T-by-1 cell vector. Y{t} contains an n_t-dimensional vector of observations for period t, where t = 1, ..., T. For linear observation models, the corresponding dimensions of the coefficient matrices, outputs of Mdl.ParamMap, C{t}, and D{t} must be consistent with the matrix in Y{t} for all periods. For nonlinear observation models, the dimensions of the inputs and outputs associated with the observations must be consistent. Regardless of model type, the last cell of Y contains the latest observations.

NaN elements indicate missing observations. For details on how simsmooth accommodates missing observations, see Algorithms.

Data Types: double | cell

`params` — State-space model parameters Θ
numeric vector

State-space model parameters Θ to evaluate the parameter mapping Mdl.ParamMap, specified as a numparams-by-1 numeric vector. Elements of params must correspond to the elements of the first input arguments of Mdl.ParamMap and Mdl.ParamDistribution.

Data Types: double

Name-Value Arguments

collapse all

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: simsmooth(Mdl,Y,params,NumParticles=1e4,Resample="residual") specifies generating 1e4 random paths and to use the residual-resampling SMC method.

`NumParticles` — Number of particles
`1000` (default) | positive integer

Number of particles for SMC, specified as a positive integer.

Example: NumParticles=1e4

Data Types: double

`NewSamples` — SMC proposal distribution
`"bootstrap"` (default) | `"optimal"` | `"unscented"` | character vector

Since R2025a

SMC proposal (importance) distribution, specified as a value in this table.

Value SMC Sampler Description

Value	SMC Sampler	Description
`"bootstrap"`	Bootstrap forward filter [7]	SMC samples particles form the state transition distribution (observations do not inform the sampler). This option is available only for models with observation noise (nonzero `D`). This method has a relatively low computational cost, but it does not inform the routine of the current observations, which can increase the Monte Carlo sampling variance.
`"optimal"`	Conditionally optimal proposal [4]	SMC samples particles from the one-step filtering distribution with incremental weights proportional to the likelihood (observations inform the sampler). The weights have minimum variance. This option is available for the following tractable models supplied in equation form: Nonlinear state transition equation and a linear measurement equation Nonlinear model with deterministic state transition equation (`B = 0`)
`"unscented"`	Unscented transformation [9]	SMC proposal distribution is the one-step filtering distribution approximated by the unscented transformation (observations inform the sampler). This option is available only for models in equation form with observation noise (nonzero `D`). By default, this option uses the filtered state mean as the representative point, around which the algorithm generates sigma points. To specify all particles as representative points for the unscented transformation, set `MultiPassUnscented=true`. This setting provides a higher-quality proposal, but it is more computationally expensive.

"bootstrap"

Bootstrap forward filter [7]

SMC samples particles form the state transition distribution (observations do not inform the sampler).

This option is available only for models with observation noise (nonzero D).

This method has a relatively low computational cost, but it does not inform the routine of the current observations, which can increase the Monte Carlo sampling variance.

"optimal"

Conditionally optimal proposal [4]

SMC samples particles from the one-step filtering distribution with incremental weights proportional to the likelihood (observations inform the sampler). The weights have minimum variance.

This option is available for the following tractable models supplied in equation form:

Nonlinear state transition equation and a linear measurement equation
Nonlinear model with deterministic state transition equation (B = 0)

"unscented"

Unscented transformation [9]

SMC proposal distribution is the one-step filtering distribution approximated by the unscented transformation (observations inform the sampler).

This option is available only for models in equation form with observation noise (nonzero D).

By default, this option uses the filtered state mean as the representative point, around which the algorithm generates sigma points. To specify all particles as representative points for the unscented transformation, set MultiPassUnscented=true. This setting provides a higher-quality proposal, but it is more computationally expensive.

Example: NewSamples="unscented"

Data Types: char | string

`MultiPassUnscented` — Flag to apply unscented transformation to all particles
`false` (default) | `true`

Since R2025a

Flag to apply unscented transformation to all particles, specified as a value in this table.

Value Description

Value	Description
`false`	The filtered state mean is the representative point, around which the algorithm generates sigma points. This option is less computationally expensive than `MultiPassUnscented=true`, but it can yield a lower-quality proposal distribution.
`true`	All particles are the representative points. This option is more computationally expensive than the default, but it can yield a higher-quality proposal distribution.

false

The filtered state mean is the representative point, around which the algorithm generates sigma points.

This option is less computationally expensive than MultiPassUnscented=true, but it can yield a lower-quality proposal distribution.

true

All particles are the representative points.

This option is more computationally expensive than the default, but it can yield a higher-quality proposal distribution.

Example: MultiPassUnscented=false

Data Types: logical

`NumPaths` — Number of sample state paths
`1` (default) | positive integer

Number of sample state paths to draw from the posterior smoothed state distribution, specified as a positive integer.

Example: NumPaths=1e4

Data Types: double

`MaxIterations` — Maximum number of rejection sampling iterations
`10` (default) | nonnegative integer

Maximum number of rejection sampling iterations for posterior sampling using the simulation smoother, specified as a nonnegative integer. simsmooth conducts rejection sampling before it conducts the computationally intensive importance sampling algorithm.

Example: MaxIterations=100

Data Types: double

`Resample` — SMC resampling method
`"multinomial"` (default) | `"residual"` | `"systematic"`

SMC resampling method, specified as a value in this table.

Value	Description
`"multinomial"`	At time t, the set of previously generated particles (parent set) follows a standard multinomial distribution, with probabilities proportional to their weights. An offspring set is resampled with replacement from the parent set [1].
`"residual"`	Residual sampling, a modified version of multinomial resampling that can produce an estimator with lower variance than the multinomial resampling method [8].
`"systematic"`	Systematic sampling, which produces an estimator with lower variance than the multinomial resampling method [3].

Resampling methods downsample insignificant particles to achieve a smaller estimator variance than if no resampling is performed and to avoid sampling from a degenerate proposal [5].

Example: Resample="residual"

Data Types: char | string

`Cutoff` — Effective sample size threshold for resampling
`0.5*NumParticles` (default) | nonnegative scalar

Effective sample size threshold, below which simsmooth resamples particles, specified as a nonnegative scalar. For more details, see [5], Ch. 12.3.3.

Tip

To resample during every period, set Cutoff=numparticles, where numparticles is the value of the NumParticles name-value argument.
To avoid resampling, set Cutoff=0.

Example: Cutoff=0.75*numparticles

Data Types: double

`SortParticles` — Flag for sorting particles before resampling
`false` (default) | `true`

Flag for sorting particles before resampling, specified as a value in this table.

Value	Description
`true`	`simsmooth` sorts the generated particles before resampling them.
`false`	`simsmooth` does not sort the generated particles.

When SortPartiles=true, simsmooth uses Hilbert sorting during the SMC routine to sort the particles. This action can reduce Monte Carlo variation, which is useful when you compare loglikelihoods resulting from evaluating several params arguments that are close to each other [3]. However, the sorting routine requires more computation resources, and can slow down computations, particularly in problems with a high-dimensional state variable.

Example: SortParticles=true

Data Types: logical

`RND` — Previously generated normal random numbers
structure array

Previously generated normal random numbers, as returned by filter, to reproduce simsmooth results, specified as the RND output, a structure array, of previous filter call. Specify RND to control the random number generator.

The default is an empty structure array, which causes simsmooth to generate new random numbers.

Data Types: struct

Output Arguments

collapse all

`X` — Simulated paths of smoothed states
numeric matrix | 3-D numeric array | cell vector of numeric matrices

Simulated paths of smoothed states, drawn from the posterior smoothed state distribution p(x_T,…,x₀|y_T,…,y₁,Θ), for t = 1,…,T, returned as a T-by-m numeric matrix for one simulated path, T-by-m-by-NumPaths 3-D numeric array for NumPaths simulated paths, or a T-by-1 cell vector of numeric matrices.

Each row corresponds to a time point in the sample. The last row contains the latest simulated smoothed states.

If Mdl is a time-invariant model with respect to the states, each column of X corresponds to a state in the model and each page corresponds to a sample path.

If Mdl is a time-varying model with respect to the states, then, for each t = 1,…,T, cell X(t) contains an m_t-by-NumPaths matrix of simulated smoothed states. Each row corresponds to a state variable for the corresponding time and each column corresponds to a simulated path. Each path across all cells correspond.

`OutputFilter` — SMC forward filtering results by sampling time
structure array

SMC forward filtering results by period, returned as a T-by-1 structure array with fields in this table, and where cell t corresponds to the filtering result for time t.

Field	Description	Estimate/Approximation of
`LogLikelihood`	Scalar approximate loglikelihood objective function value	log p(y_t\|y₁,…,y_t)
`FilteredStates`	m_t-by-1 vector of approximate filtered state estimates	$E (x_{t} \| y_{1}, ..., y_{t})$
`FilteredStatesCov`	m_t-by-m_t variance-covariance matrix of filtered states	$V a r (x_{t} \| y_{1}, ..., y_{t})$
`CustomStatistics`	(m_t + 1)-by-`NumParticles` simulated particles and corresponding weights that approximate the filtering distribution	N/A
`EffectiveSampleSize`	Effective sample size for importance sampling, a scalar in [0,`NumParticles`]	N/A
`DataUsed`	h_t-by-1 flag indicating whether the software filters using a particular observation. For example, if observation j at time t is a `NaN`, element j in `DataUsed` at time t is `0`.	N/A
`Resampled`	Flag indicating whether `simsmooth` resampled particles	N/A

`x0` — Simulated paths of smoothed initial state vector
numeric vector | numeric matrix

Simulated paths of the smoothed initial state vector, drawn from the posterior smoothed state distribution p(x_T,…,x₀|y_T,…,y₁,Θ), for t = 1,…,T, returned as an m₀-by-1 numeric vector for one simulated path or an m₀-by-NumPaths numeric matrix for NumPaths simulated paths.

Each row of x0 corresponds to a state in the model and each column corresponds to a sample path.

If you do not request to return x0, simsmooth does not compute it.

Tips

Smoothing has several advantages over filtering.
- The smoothed state estimator is more accurate than the online filter state estimator because it is based on the full-sample data, rather than only observations up to the estimated sampling time.
- A stable approximation to the gradient of the loglikelihood function, which is important for numerical optimization, is available from the smoothed state samples of the simulation smoother (finite differences of the approximated loglikelihood computed from the filter state estimates is numerically unstable).
- You can use the simulation smoother to perform Bayesian estimation of the nonlinear state-space model via the Metropolis-within-Gibbs sampler.
Unless you set Cutoff=0, simsmooth resamples particles according to the specified resampling method Resample. Although resampling particles with high weights improves the results of the SMC, you should also allow the sampler traverse the proposal distribution to obtain novel, high-weight particles. To do this, experiment with Cutoff.
Avoid an arbitrary choice of the initial state distribution. bnlssm functions generate the initial particles from the specified initial state distribution, which impacts the performance of the nonlinear filter. If the initial state specification is bad enough, importance weights concentrate on a small number of particles in the first SMC iteration, which might produce unreasonable filtering results. This vulnerability of the nonlinear model behavior contrasts with the stability of the Kalman filter for the linear model, in which the initial state distribution usually has little impact on the filter because the prior is washed out as it processes data.

Algorithms

simsmooth accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.

References

[1] Andrieu, Christophe, Arnaud Doucet, and Roman Holenstein. "Particle Markov Chain Monte Carlo Methods." Journal of the Royal Statistical Society Series B: Statistical Methodology 72 (June 2010): 269–342. https://doi.org/10.1111/j.1467-9868.2009.00736.x.

[2] Andrieu, Christophe, and Gareth O. Roberts. "The Pseudo-Marginal Approach for Efficient Monte Carlo Computations." Ann. Statist. 37 (April 2009): 697–725. https://dx.doi.org/10.1214/07-AOS574.

[3] Deligiannidis, George, Arnaud Doucet, and Michael Pitt. "The Correlated Pseudo-Marginal Method." Journal of the Royal Statistical Society, Series B: Statistical Methodology 80 (June 2018): 839–870. https://doi.org/10.1111/rssb.12280.

[4] Doucet, Arnaud, Simon Godsill, and Christophe Andrieu. "On Sequential Monte Carlo Sampling Methods for Bayesian Filtering." Statistics and Computing 10 (July 2000): 197–208. https://doi.org/10.1023/A:1008935410038.

[5] Durbin, J, and Siem Jan Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.

[6] Fernández-Villaverde, Jesús, and Juan F. Rubio-Ramírez. "Estimating Macroeconomic Models: A Likelihood Approach." Review of Economic Studies 70(October 2007): 1059–1087. https://doi.org/10.1111/j.1467-937X.2007.00437.x.

[7] Gordon, Neil J., David J. Salmond, and Adrian F. M. Smith. "Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation." IEE Proceedings F Radar and Signal Processing 140 (April 1993): 107–113. https://doi.org/10.1049/ip-f-2.1993.0015.

[8] Liu, Jun, and Rong Chen. "Sequential Monte Carlo Methods for Dynamic Systems." Journal of the American Statistical Association 93 (September 1998): 1032–1044. https://dx.doi.org/10.1080/01621459.1998.10473765.

[9] van der Merwe, Rudolph, Arnaud Doucet, Nando de Freitas, and Eric Wan. "The Unscented Particle Filter." Advances in Neural Information Processing Systems 13 (November 2000). https://dl.acm.org/doi/10.5555/3008751.3008833.

Version History

Introduced in R2024a

expand all

R2025a: Sample from posterior distribution using conditionally optimal or unscented kernel sampler

While the SMC routine implements forward filtering, it resamples particles to align them to the target distribution. The NewSamples name-value argument enables you to choose how the SMC sampler chooses the particles. The supported algorithms are the bootstrap forward filter ("bootstrap"), the conditionally optimal proposal ("optimal"), and the unscented transformation ("unscented).

By default, the unscented transformation uses the filtered state mean as the representative point, around which sigma points are generated. The MultiPassUnscented name-value argument enables you to specify all particles as representative points for the unscented transformation.

Before R2025a, the functions implement forward filtering using only the bootstrap filter.

simsmooth

Syntax

Description

Examples

Draw Path from Posterior Smoothed State Distribution

Estimate Model Parameters Using Gibbs Sampler

Monitor Underlying Sampling Procedures

Compare SMC Proposal Methods

Input Arguments

`Mdl` — Bayesian nonlinear state-space model
`bnlssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params` — State-space model parameters Θ
numeric vector

Name-Value Arguments

`NumParticles` — Number of particles
`1000` (default) | positive integer

`NewSamples` — SMC proposal distribution
`"bootstrap"` (default) | `"optimal"` | `"unscented"` | character vector

`MultiPassUnscented` — Flag to apply unscented transformation to all particles
`false` (default) | `true`

`NumPaths` — Number of sample state paths
`1` (default) | positive integer

`MaxIterations` — Maximum number of rejection sampling iterations
`10` (default) | nonnegative integer

`Resample` — SMC resampling method
`"multinomial"` (default) | `"residual"` | `"systematic"`

`Cutoff` — Effective sample size threshold for resampling
`0.5*NumParticles` (default) | nonnegative scalar

`SortParticles` — Flag for sorting particles before resampling
`false` (default) | `true`

`RND` — Previously generated normal random numbers
structure array

Output Arguments

`X` — Simulated paths of smoothed states
numeric matrix | 3-D numeric array | cell vector of numeric matrices

`OutputFilter` — SMC forward filtering results by sampling time
structure array

`x0` — Simulated paths of smoothed initial state vector
numeric vector | numeric matrix

Tips

Algorithms

References

Version History

R2025a: Sample from posterior distribution using conditionally optimal or unscented kernel sampler

See Also

Objects

Functions

simsmooth

Syntax

Description

Examples

Draw Path from Posterior Smoothed State Distribution

Estimate Model Parameters Using Gibbs Sampler

Monitor Underlying Sampling Procedures

Compare SMC Proposal Methods

Input Arguments

Mdl — Bayesian nonlinear state-space model bnlssm model object

Y — Observed response data numeric matrix | cell vector of numeric vectors

params — State-space model parameters Θ numeric vector

Name-Value Arguments

NumParticles — Number of particles 1000 (default) | positive integer

NewSamples — SMC proposal distribution "bootstrap" (default) | "optimal" | "unscented" | character vector

MultiPassUnscented — Flag to apply unscented transformation to all particles false (default) | true

NumPaths — Number of sample state paths 1 (default) | positive integer

MaxIterations — Maximum number of rejection sampling iterations 10 (default) | nonnegative integer

Resample — SMC resampling method "multinomial" (default) | "residual" | "systematic"

Cutoff — Effective sample size threshold for resampling 0.5*NumParticles (default) | nonnegative scalar

SortParticles — Flag for sorting particles before resampling false (default) | true

RND — Previously generated normal random numbers structure array

Output Arguments

X — Simulated paths of smoothed states numeric matrix | 3-D numeric array | cell vector of numeric matrices

OutputFilter — SMC forward filtering results by sampling time structure array

x0 — Simulated paths of smoothed initial state vector numeric vector | numeric matrix

Tips

Algorithms

References

Version History

R2025a: Sample from posterior distribution using conditionally optimal or unscented kernel sampler

See Also

Objects

Functions

`Mdl` — Bayesian nonlinear state-space model
`bnlssm` model object

`Y` — Observed response data
numeric matrix | cell vector of numeric vectors

`params` — State-space model parameters Θ
numeric vector

`NumParticles` — Number of particles
`1000` (default) | positive integer

`NewSamples` — SMC proposal distribution
`"bootstrap"` (default) | `"optimal"` | `"unscented"` | character vector

`MultiPassUnscented` — Flag to apply unscented transformation to all particles
`false` (default) | `true`

`NumPaths` — Number of sample state paths
`1` (default) | positive integer

`MaxIterations` — Maximum number of rejection sampling iterations
`10` (default) | nonnegative integer

`Resample` — SMC resampling method
`"multinomial"` (default) | `"residual"` | `"systematic"`

`Cutoff` — Effective sample size threshold for resampling
`0.5*NumParticles` (default) | nonnegative scalar

`SortParticles` — Flag for sorting particles before resampling
`false` (default) | `true`

`RND` — Previously generated normal random numbers
structure array

`X` — Simulated paths of smoothed states
numeric matrix | 3-D numeric array | cell vector of numeric matrices

`OutputFilter` — SMC forward filtering results by sampling time
structure array

`x0` — Simulated paths of smoothed initial state vector
numeric vector | numeric matrix