filter
Forward recursion of diffuse state-space models
Description
X = filter(Mdl,Y)X)
by performing forward recursion of the fully specified diffuse state-space
model Mdl. That is, filter applies
the diffuse Kalman filter using Mdl and
the observed responses Y.
X = filter(Mdl,Y,Name,Value)Name,Value pair
arguments. For example, specify the regression coefficients and predictor
data to deflate the observations, or specify to use the univariate
treatment of a multivariate model.
If Mdl is not fully specified, then you must
specify the unknown parameters as known scalars using the 'Params' Name,Value pair
argument.
[ additionally returns the loglikelihood
value (X,logL,Output]
= filter(___)logL) and an output structure array (Output)
using any of the input arguments in the previous syntaxes. Output contains:
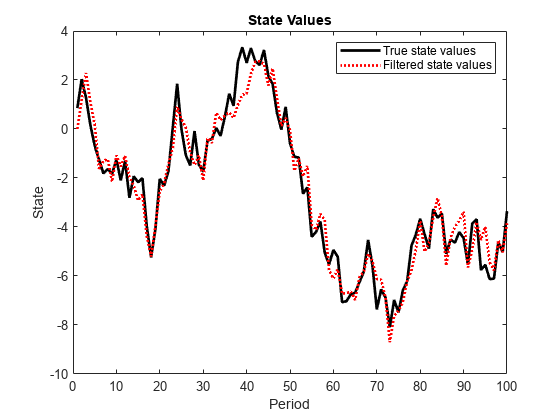
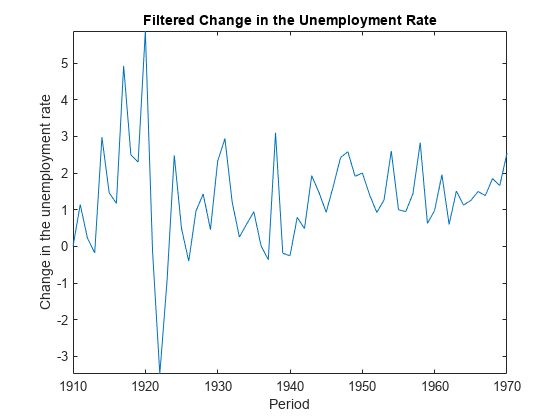
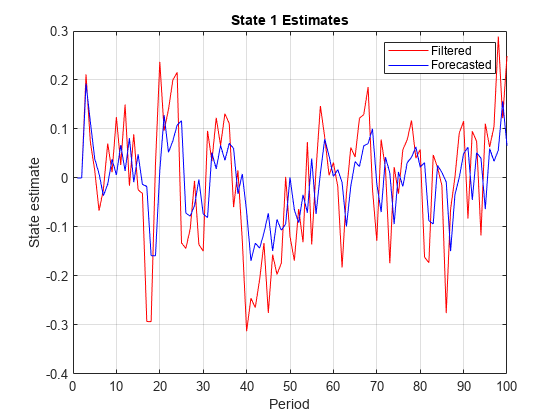
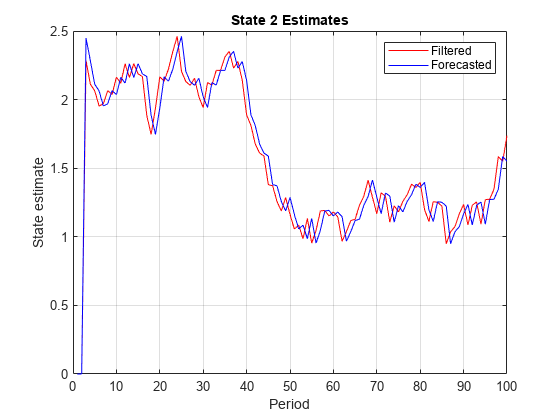
Filtered and forecasted states
Estimated covariance matrices of the filtered and forecasted states
Loglikelihood value
Forecasted observations and its estimated covariance matrix
Adjusted Kalman gain
Vector indicating which data the software used to filter
Input Arguments
Name-Value Arguments
Output Arguments
Examples
Tips
Mdldoes not store the response data, predictor data, and the regression coefficients. Supply the data wherever necessary using the appropriate input or name-value pair arguments.It is a best practice to allow
filterto determine the value ofSwitchTime. However, in rare cases, you might experience numerical issues during estimation, filtering, or smoothing diffuse state-space models. For such cases, try experimenting with variousSwitchTimespecifications, or consider a different model structure (e.g., simplify or reverify the model). For example, convert the diffuse state-space model to a standard state-space model usingssm.To accelerate estimation for low-dimensional, time-invariant models, set
'Univariate',true. Using this specification, the software sequentially updates rather then updating all at once during the filtering process.
Algorithms
The Kalman filter accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.
For explicitly defined state-space models,
filterapplies all predictors to each response series. However, each response series has its own set of regression coefficients.The diffuse Kalman filter requires presample data. If missing observations begin the time series, then the diffuse Kalman filter must gather enough nonmissing observations to initialize the diffuse states.
For diffuse state-space models,
filterusually switches from the diffuse Kalman filter to the standard Kalman filter when the number of cumulative observations and the number of diffuse states are equal. However, if a diffuse state-space model has identifiability issues (e.g., the model is too complex to fit to the data), thenfiltermight require more observations to initialize the diffuse states. In extreme cases,filterrequires the entire sample.
References
[1] Durbin J., and S. J. Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.
Version History
Introduced in R2015b