Estimate Random Parameter of State-Space Model

Simulate Data

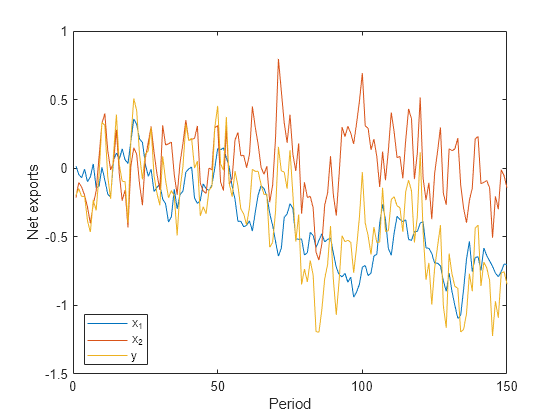
Simulate 100 years of net exports from:

rng(100); % For reproducibility
T = 150;
sigma1 = 0.1;
sigma2 = 0.2;
phi = 0.6;

u1 = randn(T,1)*sigma1;
x1 = cumsum(u1);
Mdl2 = arima('AR',phi,'Variance',sigma2^2,'Constant',0);
x2 = simulate(Mdl2,T,'Y0',0);
y = x1 + x2;

figure;
plot([x1 x2 y])
legend('x_1','x_2','y','Location','Best');
ylabel('Net exports');
xlabel('Period');

The Zig-Zag Estimation Method

Treat $$\varphi$$ as if it is unknown and random, and use the zig-zag method to recover its distribution. To implement the zig-zag method:

1. Choose an initial value for $$\varphi$$ in the interval (-1,1), and denote it $${\varphi }_z$$.

2. Create the true state-space model, that is, an ssm model object that represents the data-generating process.

3. Use the simulation smoother (simsmooth) to draw a random path from the distribution of the second smoothed states. Symbolically, $$x_{2,z,t}\sim P(x_{2,t}|y_t,x_{1,t},\varphi ={\varphi }_z)$$.

4. Create another state-space model that has this form

In words, $${\varphi }_{z,t}$$ is a static state and $$x_{2,z,t}$$ is an "observed" series with time varying coefficient $$C_t=x_{2,z,t-1}$$.

5. Use the simulation smoother to draw a random path from the distribution of the smoothed $${\varphi }_{z,t}$$ series. Symbolically, $${\varphi }_{z,t}\sim P(\varphi |x_{2,z,t})$$, where $$x_{2,z,t}$$ encompasses the structure of the true state-space model and the observations. $${\varphi }_{z,t}$$ is static, so you can just reserve one value ($${\varphi }_z$$).

6. Repeat steps 2 - 5 many times and store $${\varphi }_z$$ each iteration.

7. Perform diagnostic checks on the simulation series. That is, construct:

8. The remaining series represents draws from the posterior distribution of $$\varphi$$. You can compute descriptive statistics, or plot a histogram to determine the qualities of the distribution.

Estimate Random Coefficient Using Zig-Zag Method

Specify initial values, preallocate, and create the true state-space model.

phi0 = -0.3;             % Initial value of phi
Z = 1000;                % Number of times to iterate the zig-zag method
phiz = [phi0; nan(Z,1)]; % Preallocate

A = [1 0; 0 NaN];
B = [sigma1; sigma2];
C = [1 1];
Mdl = ssm(A,B,C,'StateType',[2; 0]);

Mdl is an ssm model object. The NaN acts as a placeholder for $$\varphi$$.

Iterate steps 2 - 5 of the zig-zag method.

for j = 2:(Z + 1);
    % Draw a random path from smoothed x_2 series.
    xz = simsmooth(Mdl,y,'Params',phiz(j-1));
    % The second column of xz is a draw from the posterior distribution of x_2.
    
    % Create the intermediate state-space model.
    Az = 1;
    Bz = 0;
    Cz = num2cell(xz((1:(end - 1)),2));
    Dz = sigma2;
    Mdlz = ssm(Az,Bz,Cz,Dz,'StateType',2);
    
    % Draw a random path from the smoothed phiz series.
    phizvec = simsmooth(Mdlz,xz(2:end,2));
    phiz(j) = phizvec(1);
    % phiz(j) is a draw from the posterior distribution of phi
end

phiz is a Markov chain. Before analyzing the posterior distribution of $$\varphi$$, you should assess whether to impose a burn-in period, or the severity of the autocorrelation in the chain.

Determine Quality of Simulation

Draw a trace plot for the first 100, 500, and all of the random draws.

vec = [100 500 Z];
figure;
for j = 1:3;
    subplot(3,1,j)
    plot(phiz(1:vec(j)));
    title('Trace Plot for \phi');
    xlabel('Simulation number');
    axis tight;
end

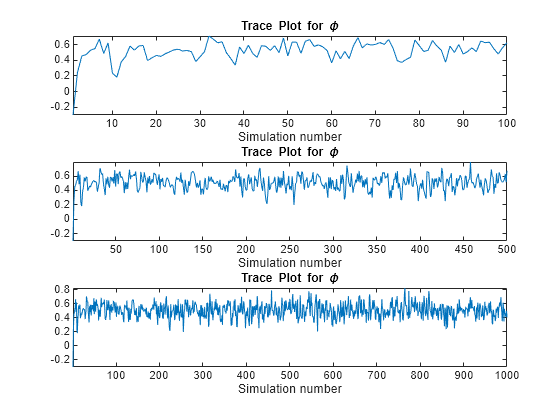
According to the first plot, transient effects die down after about 20 draws. Therefore, a short burn-in period should suffice. The plot of the entire simulation shows that the series settles around a center.

Plot the autocorrelation function of the series after removing the first 20 draws.

burnOut = 21:Z;

figure;
autocorr(phiz(burnOut));

The autocorrelation function dies out rather quickly. It doesn't seem like autocorrelation in the chain is an issue.

Determine qualities of the posterior distribution of $$\varphi$$ by computing simulation statistics and by plotting a histogram of the reduced set of random draws.

xbar = mean(phiz(burnOut))

xbar = 
0.5104

xstd = std(phiz(burnOut))

xstd = 
0.0988

ci = norminv([0.025,0.975],xbar,xstd); % 95% confidence interval

figure;
histogram(phiz(burnOut),'Normalization','pdf');
h = gca;
hold on;
simX = linspace(h.XLim(1),h.XLim(2),100);
simPDF = normpdf(simX,xbar,xstd); 
plot(simX,simPDF,'k','LineWidth',2);
h1 = plot([xbar xbar],h.YLim,'r','LineWidth',2);
h2 = plot([0.6 0.6],h.YLim,'g','LineWidth',2);
h3 = plot([ci(1) ci(1)],h.YLim,'--r',...
    [ci(2) ci(2)],h.YLim,'--r','LineWidth',2);
legend([h1 h2 h3(1)],{'Simulation Mean','True Mean','95% CI'});
h.XTick = sort([h.XTick xbar]);
h.XTickLabel{h.XTick == xbar} = xbar;
h.XTickLabelRotation = 90;

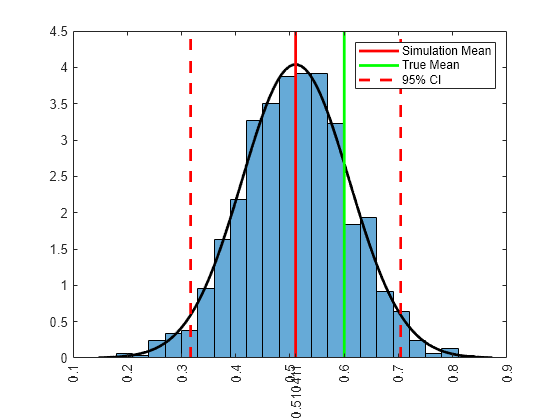
The posterior distribution of $$\varphi$$ is roughly normal with mean and standard deviation approximately 0.51 and 0.1, respectively. The true mean of $$\varphi$$ is 0.6, and it is less than one standard deviation to the right of the simulation mean.

Compute the maximum likelihood estimate of $$\varphi$$. That is, treat $$\varphi$$ as a fixed, but unknown parameter, and then estimate Mdl using the Kalman filter and maximum likelihood.

[~,estParams] = estimate(Mdl,y,phi0)

Method: Maximum likelihood (fminunc)
Sample size: 150
Logarithmic  likelihood:     -10.1434
Akaike   info criterion:      22.2868
Bayesian info criterion:      25.2974
      |     Coeff       Std Err     t Stat       Prob  
-------------------------------------------------------
 c(1) |  0.53590       0.19183    2.79360      0.00521 
      |                                                
      |   Final State   Std Dev    t Stat        Prob  
 x(1) | -0.85059       0.00000   -6.45811e+08   0      
 x(2) |  0.00454        0          Inf          0      

estParams = 
0.5359

The MLE of $$\varphi$$ is 0.54. Both estimates are within one standard deviation or standard error from the true value of $$\varphi$$.