filter

Filter disturbances through conditional variance model

Syntax

[V,Y] =
filter(Mdl,Z)

Tbl2 = filter(Mdl,Tbl1)

[___] = filter(___,Name,Value)

Description

[V,Y] = filter(Mdl,Z) returns the numeric arrays of conditional variance paths V and response paths Y from filtering the numeric array of disturbance paths Z through the fully specified conditional variance model Mdl. Mdl can be a garch, egarch, or gjr model.

example

Tbl2 = filter(Mdl,Tbl1) returns the table or timetable Tbl2 containing the results from filtering the paths of disturbances in the input table or timetable Tbl1 through Mdl. The disturbance variable in Tbl1 is associated with the model innovations process through Mdl. (since R2023a)

filter selects the response variable named in Mdl.SeriesName or the sole variable in Tbl1. To select a different disturbance variable in Tbl1 to filter through the model, use the DisturbanceVariable name-value argument.

example

[___] = filter(___,Name,Value) specifies options using one or more name-value arguments in addition to any of the input argument combinations in previous syntaxes. filter returns the output argument combination for the corresponding input arguments. For example, filter(Mdl,Z,Z0=PS) filters the numeric vector of disturbances Z through the conditional variance model Mdl and specifies the numeric vector of presample disturbance data PS to initialize the model.

example

Examples

collapse all

Filter Numeric Vector Containing Disturbance Path

Open Live Script

Demonstrate that simulate and filter can return equal quantities. Supply data in a numeric vector.

Specify a GARCH(1,1) model with Gaussian innovations.

Mdl = garch(Constant=0.005,GARCH=0.8,ARCH=0.1);

Simulate the model using Monte Carlo simulation. Then, standardize the simulated innovations and filter them.

rng(1) % For reproducibility
[vs,es] = simulate(Mdl,100,E0=0,V0=0.05);
Z = es./sqrt(vs);
[vf,ef] = filter(Mdl,Z,Z0=0,V0=0.05);

Confirm that the outputs of simulate and filter are identical.

norm(vs-vf)

ans = 
0

A norm of 0 indicates that the two outputs are identical.

Filter Timetable of Disturbance Data Through GARCH Model

Since R2023a

Open Live Script

Fit a GARCH(1,1) model to the average weekly closing NASDAQ returns, and then filter a randomly generated series of disturbances through the estimated model. Supply timetables of data throughout the process.

Load the U.S. equity indices data Data_EquityIdx.mat.

load Data_EquityIdx

The timetable DataTimeTable contains the daily NASDAQ closing prices, among other indices.

Compute the weekly average closing prices of all timetable variables.

DTTW = convert2weekly(DataTimeTable,Aggregation="mean");

Compute the weekly returns.

DTTRet = price2ret(DTTW);
DTTRet.Interval = [];
T = height(DTTRet)

T = 
626

Plot the weekly NASDAQ returns.

figure
plot(DTTRet.Time,DTTRet.NASDAQ)
title("NASDAQ Weekly Returns")

Figure contains an axes object. The axes object with title NASDAQ Weekly Returns contains an object of type line.

The returns exhibit volatility clustering.

When you plan to supply a timetable, you must ensure it has all the following characteristics:

The selected response variable is numeric and does not contain any missing values.
The timestamps in the Time variable are regular, and they are ascending or descending.

Remove all missing values from the timetable, relative to the NASDAQ returns series.

DTTRet = rmmissing(DTTRet,DataVariables="NASDAQ");
numobs = height(DTTRet)

numobs = 
626

Because all sample times have observed NASDAQ returns, rmmissing does not remove any observations.

Determine whether the sampling timestamps have a regular frequency and are sorted.

areTimestampsRegular = isregular(DTTRet,"weeks")

areTimestampsRegular = logical
   1

areTimestampsSorted = issorted(DTTRet.Time)

areTimestampsSorted = logical
   1

areTimestampsRegular = 1 indicates that the timestamps of DTTRet represent a regular weekly sample. areTimestampsSorted = 1 indicates that the timestamps are sorted.

Specify a GARCH(1,1) model, and fit it to the series. Name the response series of the model NASDAQ by using dot notation.

Mdl = garch(1,1);
Mdl.SeriesName = "NASDAQ";
EstMdl = estimate(Mdl,DTTRet);

 
    GARCH(1,1) Conditional Variance Model (Gaussian Distribution):
 
                  Value       StandardError    TStatistic      PValue  
                __________    _____________    __________    __________

    Constant    1.7406e-06     8.9077e-07        1.9541        0.050694
    GARCH{1}       0.65947       0.059314        11.118      1.0229e-28
    ARCH{1}        0.33773       0.079595        4.2431      2.2044e-05

estimate fits the model to the response data in the NASDAQ variable of DTTRet because the name matches the name of the response variable in Mdl.SeriesName. Alternatively, you can specify the response variable by using the ResponseVariable name-value argument.

Generate 2 random, independent series of length T from the standard Gaussian distribution. Store the matrix of series as one variable in DTTRet.

rng(1) % For reproducibility
DTTRet.Z = randn(T,2);

DTTRet contains a new variable called Z containing a T-by-2 matrix of five disturbance paths.

Filter the paths of disturbances through the estimated GARCH model. Specify the table variable name containing the disturbance paths.

Tbl2 = filter(EstMdl,DTTRet,DisturbanceVariable="Z")

Tbl2=626×5 timetable
       Time           NYSE          NASDAQ                 Z                  NASDAQ_Variance             NASDAQ_Response     
    ___________    ___________    ___________    _____________________    ________________________    ________________________

    12-Jan-1990     -0.0031597     -0.0026701    -0.64901     -0.50964    0.00059062    0.00045179     -0.015773     -0.010833
    19-Jan-1990     -0.0038123     -0.0039103      1.1812     0.088893    0.00047526    0.00033931       0.02575     0.0016374
    26-Jan-1990     -0.0040706     -0.0039139    -0.75845    -0.019698    0.00053909    0.00022641      -0.01761    -0.0002964
    02-Feb-1990    -0.00099691     -0.0033847     -1.1096     -0.73807    0.00046199    0.00015108      -0.02385     -0.009072
    09-Feb-1990      0.0022796      0.0031891    -0.84555      -1.1522    0.00049852    0.00012917     -0.018879     -0.013095
    16-Feb-1990    -0.00021948     0.00037747    -0.57266      -1.9476    0.00045087    0.00014483      -0.01216     -0.023439
    23-Feb-1990     -0.0022725     -0.0018693    -0.55868     0.026296    0.00034901     0.0002828     -0.010437    0.00044221
    02-Mar-1990      0.0019481      0.0012208     0.17838     -0.82589    0.00026869     0.0001883      0.002924     -0.011333
    09-Mar-1990      0.0022677      0.0026984    -0.19686     -0.71799    0.00018182     0.0001693    -0.0026545    -0.0093421
    16-Mar-1990     0.00029781      0.0012667     0.58644       -1.941    0.00012403    0.00014286      0.006531       -0.0232
    23-Mar-1990     0.00027271     0.00042646    -0.85189      0.98755    9.7937e-05    0.00027773    -0.0084306      0.016458
    30-Mar-1990     0.00022176    -0.00052576     0.80032      -1.6631    9.0331e-05    0.00027637     0.0076065     -0.027648
    06-Apr-1990     0.00016495     -0.0010113     -1.5094       2.0633    8.0852e-05    0.00044216     -0.013572      0.043387
    13-Apr-1990     0.00050551    -0.00037366     0.87587       -2.082    0.00011727    0.00092908      0.009485     -0.063462
    20-Apr-1990    -0.00072855    -0.00042758    -0.24279      0.27316    0.00010946     0.0019746    -0.0025402      0.012138
    27-Apr-1990     -0.0039166     -0.0039974     0.16681      -2.3767    7.6106e-05     0.0013537     0.0014553     -0.087447
      ⋮

Tbl2 is a 626-by-5 timetable containing all variables in DTTRet, the two filtered conditional variance paths NASDAQ_Variance, and the two filtered response paths NASDAQ_Response.

Filter Multiple Disturbance Paths Through EGARCH Model

Open Live Script

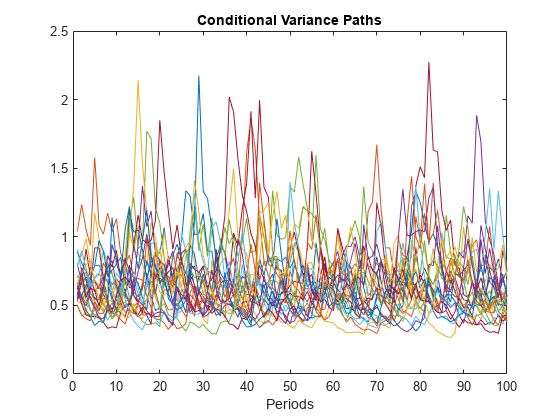
Specify an EGARCH(1,1) model with Gaussian innovations.

Mdl = egarch(Constant=-0.1,GARCH=0.8,ARCH=0.3, ...
    Leverage=-0.05);

Simulate 25 series of standard Gaussian observations for 100 periods.

rng(1); % For reproducibility
Z = randn(100,25);

Z represents 25 paths of synchronized disturbances for 100 periods.

Obtain 25 paths of conditional variances by filtering the disturbance paths through the EGARCH(1,1) model.

V = filter(Mdl,Z);

Plot the paths of conditional variances.

figure;
plot(V);
title("Conditional Variance Paths");
xlabel("Periods");

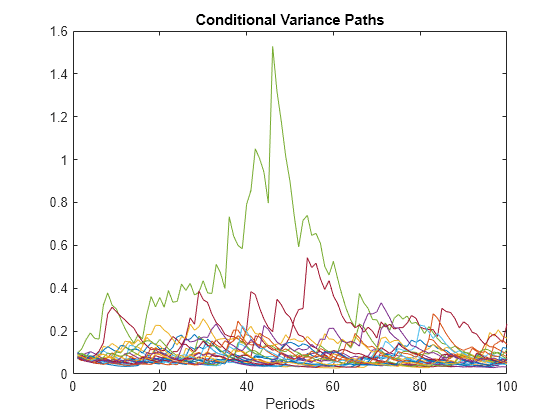
Figure contains an axes object. The axes object with title Conditional Variance Paths, xlabel Periods contains 25 objects of type line.

Filter Disturbances Through GJR Model Specifying Presample Observations

Open Live Script

Specify a GJR(1,2) model with Gaussian innovations.

Mdl = gjr(Constant=0.005,GARCH=0.8,ARCH={0.1 0.01}, ...
    Leverage={0.05 0.01});

Simulate 25 series of standard Gaussian observations for 102 periods.

rng(1); % For reproducibility
Z = randn(102,25);

Z represents 25 paths of synchronized disturbances for 102 periods.

Obtain 25, 100 period paths of conditional variances by filtering the disturbance paths through the GJR(1,2) model. Specify the first two disturbances as presample observations.

V = filter(Mdl,Z(3:end,:),Z0=Z(1:2,:));

Plot the paths of conditional variances.

figure
plot(V)
title("Conditional Variance Paths");
xlabel("Periods");

Figure contains an axes object. The axes object with title Conditional Variance Paths, xlabel Periods contains 25 objects of type line.

Input Arguments

collapse all

`Mdl` — Conditional variance model
`garch` model object | `egarch` model object | `gjr` model object

Conditional variance model without any unknown parameters, specified as a garch, egarch, or gjr model object.

Mdl cannot contain any properties that have NaN value.

`Z` — Disturbance paths z_t
numeric column vector | numeric matrix

Disturbance paths z_t used to drive the output innovation process ε_t, specified as a numobs-by-1 numeric vector or numobs-by-numpaths numeric matrix. Given the variance process σ_t², the innovation process is

$ε_{t} = σ_{t} z_{t} .$

As a column vector, Z represents a single path of the underlying disturbance series.

As a matrix, the rows of Z correspond to periods. The columns correspond to separate paths. The observations across any row occur simultaneously.

The last element or row of Z contains the latest observation.

`Tbl1` — Time series data
table | timetable

Since R2023a

Time series data containing observed disturbance variable z_t, associated with the model innovations process ε_t, specified as a table or timetable with numvars variables and numobs rows. You can optionally select a disturbance variable by using the DisturbanceVariable name-value argument.

Given the variance process σ_t², the innovation process is

$ε_{t} = σ_{t} z_{t} .$

The selected variable is a single path (numobs-by-1 vector) or multiple paths (numobs-by-numpaths matrix) of numobs observations of disturbance data. Each row is an observation, and measurements in each row occur simultaneously.

Each path (column) of the selected variable is independent of the other paths.

If Tbl1 is a timetable, it must represent a sample with a regular datetime time step (see isregular), and the datetime vector Tbl1.Time must be strictly ascending or descending.

If Tbl1 is a table, the last row contains the latest observation.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: filter(Mdl,Z,Z0=[1 1;0.5 0.5],V0=[1 0.5;1 0.5]) specifies two equivalent presample paths of disturbances and two different presample paths of conditional variances.

`DisturbanceVariable` — Variable to select from `Tbl1` to treat as disturbance variable z_t
string scalar | character vector | integer | logical vector

Since R2023a

Variable to select from Tbl1 to treat as the disturbance variable z_t to filter through Mdl, specified as one of the following data types:

String scalar or character vector containing a variable name in Tbl1.Properties.VariableNames
Variable index (positive integer) to select from Tbl1.Properties.VariableNames
A logical vector, where DisturbanceVariable(j) = true selects variable j from Tbl1.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaN).

If Tbl1 has one variable, the default specifies that variable. Otherwise, the default matches the variable to names in Mdl.SeriesName.

Example: DisturbanceVariable="StockRateDist"

Example: DisturbanceVariable=[false false true false] or DisturbanceVariable=3 selects the third table variable as the disturbance variable.

Data Types: double | logical | char | cell | string

`Z0` — Presample disturbance paths z_t
numeric column vector | numeric matrix

Presample disturbance paths z_t, specified as a numpreobs-by-1 numeric vector or numpreobs-by-numprepaths matrix. Z0 provides initial values for the input disturbance paths Z. Use Z0 only when you supply the numeric array of disturbances Z.

numpreobs is the number of presample observations. numprepaths is the number of presample response paths.

Each row is a presample observation, and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.Q. If numpreobs > Mdl.Q, filter uses the latest required number of observations only.

If Z0 is a column vector, it represents a single path of the underlying disturbance series. filter applies it to each output path.
If Z0 is a matrix, each column represents a presample path of the underlying disturbance series. numprepaths must be at least numpaths. If numprepaths > numpaths, filter uses the first size(Z,2) columns only.

By default, filter sets any necessary presample disturbances to an independent sequence of standardized disturbances drawn from Mdl.Distribution.

Data Types: double

`V0` — Positive presample conditional variance paths σ_t²
positive column vector | positive matrix

Positive presample conditional variance paths σ_t², specified as a numpreobs-by-1 positive column vector or numpreobs-by-numprepaths positive matrix. V0 provides initial values for the conditional variances in the model. Use V0 only when you supply the numeric array of disturbances Z.

To initialize the conditional variance model, numpreobs must be at least max([Mdl.P Mdl.Q]). If numpreobs > max([Mdl.P Mdl.Q]), filter uses the latest required number of observations only. The last element or row contains the latest observation.

If V0 is a column vector, it represents a single path of the conditional variance series. filter applies it to each output path.
If V0 is a matrix, numprepaths must be at least numpaths. If numprepaths > numpaths, filter uses the first size(Z,2) columns only.

By default, filter sets any necessary presample conditional variances to the unconditional variance of the process.

Data Types: double

`Presample` — Presample data
table | timetable

Since R2023a

Presample data containing paths of innovation ε_t or conditional variance σ_t² series to initialize the model, specified as a table or timetable, the same type as Tbl1, with numprevars variables and numpreobs rows. Use Presample only when you supply a table or timetable of data Tbl1.

Each selected variable is a single path (numpreobs-by-1 vector) or multiple paths (numpreobs-by-numprepaths matrix) of numpreobs observations representing the presample of the disturbance or conditional variance series for DisturbanceVariable, the selected disturbance variable in Tbl1.

Each row is a presample observation, and measurements in each row occur simultaneously. numpreobs must be one of the following values:

Mdl.Q when Presample provides only presample disturbances
max([Mdl.P Mdl.Q]) when Presample provides presample conditional variances

If you supply more rows than necessary, filter uses the latest required number of observations only.

If Presample is a timetable, all the following conditions must be true:

Presample must represent a sample with a regular datetime time step (see isregular).
The inputs Tbl1 and Presample must be consistent in time such that Presample immediately precedes Tbl1 with respect to the sampling frequency and order.
The datetime vector of sample timestamps Presample.Time must be ascending or descending.

If Presample is a table, the last row contains the latest presample observation.

By default, filter sets any necessary presample disturbances to an independent sequence of standardized disturbances drawn from Mdl.Distribution, and it sets any necessary presample conditional variances to the unconditional variance of the process characterized by Mdl.

If you specify the Presample, you must specify the presample disturbance or conditional variance names by using the PresampleDisturbanceVariable or PresampleVarianceVariable name-value argument.

`PresampleDisturbanceVariable` — Variable of `Presample` containing presample disturbance paths z_t
string scalar | character vector | integer | logical vector

Since R2023a

Variable of Presample containing presample disturbance paths z_t, specified as one of the following data types:

String scalar or character vector containing a variable name in Presample.Properties.VariableNames
Variable index (positive integer) to select from Presample.Properties.VariableNames
A logical vector, where PresampleDisturbanceVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric matrix and cannot contain missing values (NaNs).

If you specify presample disturbance data by using the Presample name-value argument, you must specify PresampleDisturbanceVariable.

Example: PresampleDisturbanceVariable="StockRateDist0"

Example: PresampleDisturbanceVariable=[false false true false] or PresampleDisturbanceVariable=3 selects the third table variable as the presample disturbance variable.

Data Types: double | logical | char | cell | string

`PresampleVarianceVariable` — Variable of `Presample` containing data for the presample conditional variances σ_t²
string scalar | character vector | integer | logical vector

Since R2023a

Variable of Presample containing data for the presample conditional variances σ_t², specified as one of the following data types:

String scalar or character vector containing a variable name in Presample.Properties.VariableNames
Variable index (positive integer) to select from Presample.Properties.VariableNames
A logical vector, where PresampleVarianceVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaNs).

If you specify presample conditional variance data by using the Presample name-value argument, you must specify PresampleVarianceVariable.

Example: PresampleVarianceVariable="StockRateVar0"

Example: PresampleVarianceVariable=[false false true false] or PresampleVarianceVariable=3 selects the third table variable as the presample conditional variance variable.

Data Types: double | logical | char | cell | string

Note

NaN values in Z, Z0, and V0 indicate missing values. filter removes missing values from specified data by list-wise deletion.
- For the presample, filter horizontally concatenates Z0 and V0, and then it removes any row of the concatenated matrix containing at least one NaN.
- For in-sample data Z, filter removes any row containing at least one NaN.
This type of data reduction reduces the effective sample size and can create an irregular time series.
For numeric data inputs, filter assumes that you synchronize the presample data such that the latest observations occur simultaneously.
filter issues an error when any table or timetable input contains missing values.

Output Arguments

collapse all

`V` — Filtered conditional variance paths σ_t²
numeric column vector | numeric matrix

Filtered conditional variance paths σ_t², returned as a numobs-by-1 numeric column vector or numobs-by-numpaths numeric matrix. V represents the conditional variances of the mean-zero, heteroscedastic innovations associated with Y. filter returns V only when you supply the input Z.

The dimensions of V and Z are equivalent. If Z is a matrix, then the columns of V are the conditional variance paths corresponding to the columns of Z.

Rows of V are periods corresponding to the periodicity of Z.

`Y` — Filtered response paths y_t
numeric column vector | numeric matrix

Filtered response paths y_t, returned as a numobs-by-1 numeric column vector or numobs-by-numpaths. Y usually represents a mean-zero, heteroscedastic time series of innovations with conditional variances given in V. filter returns Y only when you supply the input Z.

Y can also represent a time series of mean-zero, heteroscedastic innovations plus an offset. If Mdl includes an offset, then filter adds the offset to the underlying mean-zero, heteroscedastic innovations. Therefore, Y represents a time series of offset-adjusted innovations.

If Z is a matrix, then the columns of Y are the response paths corresponding to the columns of Z.

Rows of Y are periods corresponding to the periodicity of Z.

`Tbl2` — Filtered conditional variance σ_t² and response y_t paths
table | timetable

Since R2023a

Filtered conditional variance σ_t² and response y_t paths, returned as a table or timetable, the same data type as Tbl1. filter returns Tbl2 only when you supply the input Tbl1.

Tbl2 contains the following variables:

The filtered conditional variances paths, which are in a numobs-by-numpaths numeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the disturbance variable in Tbl1. filter names the filtered conditional variance variable in Tbl2 responseName_Variance, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is StockReturns, Tbl2 contains a variable for the corresponding filtered response paths with the name StockReturns_Variance.
The filtered response paths, which are in a numobs-by-numpaths numeric matrix, with rows representing observations and columns representing independent paths, each corresponding to the input observations and paths of the disturbance variable in Tbl1. filter names the filtered response variable in Tbl2 responseName_Response, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is StockReturns, Tbl2 contains a variable for the corresponding filtered conditional variance paths with the name StockReturns_Response.
All variables Tbl1.

If Tbl1 is a timetable, row times of Tbl1 and Tbl2 are equal.

Alternatives

filter generalizes simulate. Both function filter a series of disturbances to produce output responses and conditional variances. However, simulate autogenerates a series of mean-zero, unit-variance, independent and identically distributed (iid) disturbances according to the distribution in the conditional variance model object, Mdl. In contrast, filter lets you directly specify your own disturbances.

References

[1] Bollerslev, T. “Generalized Autoregressive Conditional Heteroskedasticity.” Journal of Econometrics. Vol. 31, 1986, pp. 307–327.

[2] Bollerslev, T. “A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return.” The Review of Economics and Statistics. Vol. 69, 1987, pp. 542–547.

[3] Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

[4] Enders, W. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, 1995.

[5] Engle, R. F. “Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica. Vol. 50, 1982, pp. 987–1007.

[6] Hamilton, J. D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

Version History

Introduced in R2012a

expand all

R2023a: `filter` accepts input data in tables and timetables, and returns results in tables and timetables

In addition to accepting input data (in-sample and presample) in numeric arrays, filter accepts input data in tables or regular timetables. When you supply data in a table or timetable, the following conditions apply:

filter chooses the default in-sample disturbance series on which to operate, but you can use the specified optional name-value argument to select a different series.
If you specify optional presample disturbance or conditional variance data to initialize the model, you must also specify the presample disturbance or conditional variance series name.
filter returns results in a table or timetable.

Name-value arguments to support tabular workflows include:

DisturbanceVariable specifies the variable name of the disturbance paths in the input data Tbl1 to filter through the model.
Presample specifies the input table or timetable of presample disturbance and conditional variance data.
PresampleDisturbanceVariable specifies the variable name of the disturbance paths to select from Presample.
PresampleVarianceVariable specifies the variable name of the conditional variance paths to select from Presample.

filter

Syntax

Description

Examples

Filter Numeric Vector Containing Disturbance Path

Filter Timetable of Disturbance Data Through GARCH Model

Filter Multiple Disturbance Paths Through EGARCH Model

Filter Disturbances Through GJR Model Specifying Presample Observations

Input Arguments

`Mdl` — Conditional variance model
`garch` model object | `egarch` model object | `gjr` model object

`Z` — Disturbance paths z_t
numeric column vector | numeric matrix

`Tbl1` — Time series data
table | timetable

Name-Value Arguments

`DisturbanceVariable` — Variable to select from `Tbl1` to treat as disturbance variable z_t
string scalar | character vector | integer | logical vector

`Z0` — Presample disturbance paths z_t
numeric column vector | numeric matrix

`V0` — Positive presample conditional variance paths σ_t²
positive column vector | positive matrix

`Presample` — Presample data
table | timetable

`PresampleDisturbanceVariable` — Variable of `Presample` containing presample disturbance paths z_t
string scalar | character vector | integer | logical vector

`PresampleVarianceVariable` — Variable of `Presample` containing data for the presample conditional variances σ_t²
string scalar | character vector | integer | logical vector

Output Arguments

`V` — Filtered conditional variance paths σ_t²
numeric column vector | numeric matrix

`Y` — Filtered response paths y_t
numeric column vector | numeric matrix

`Tbl2` — Filtered conditional variance σ_t² and response y_t paths
table | timetable

Alternatives

References

Version History

R2023a: `filter` accepts input data in tables and timetables, and returns results in tables and timetables

See Also

Objects

Functions

Topics

filter

Syntax

Description

Examples

Filter Numeric Vector Containing Disturbance Path

Filter Timetable of Disturbance Data Through GARCH Model

Filter Multiple Disturbance Paths Through EGARCH Model

Filter Disturbances Through GJR Model Specifying Presample Observations

Input Arguments

Mdl — Conditional variance model garch model object | egarch model object | gjr model object

Z — Disturbance paths zt numeric column vector | numeric matrix

Tbl1 — Time series data table | timetable

Name-Value Arguments

DisturbanceVariable — Variable to select from Tbl1 to treat as disturbance variable zt string scalar | character vector | integer | logical vector

Z0 — Presample disturbance paths zt numeric column vector | numeric matrix

V0 — Positive presample conditional variance paths σt2 positive column vector | positive matrix

Presample — Presample data table | timetable

PresampleDisturbanceVariable — Variable of Presample containing presample disturbance paths zt string scalar | character vector | integer | logical vector

PresampleVarianceVariable — Variable of Presample containing data for the presample conditional variances σt2 string scalar | character vector | integer | logical vector

Output Arguments

V — Filtered conditional variance paths σt2 numeric column vector | numeric matrix

Y — Filtered response paths yt numeric column vector | numeric matrix

Tbl2 — Filtered conditional variance σt2 and response yt paths table | timetable

Alternatives

References

Version History

R2023a: filter accepts input data in tables and timetables, and returns results in tables and timetables

See Also

Objects

Functions

Topics

`Mdl` — Conditional variance model
`garch` model object | `egarch` model object | `gjr` model object

`Z` — Disturbance paths z_t
numeric column vector | numeric matrix

`Tbl1` — Time series data
table | timetable

`DisturbanceVariable` — Variable to select from `Tbl1` to treat as disturbance variable z_t
string scalar | character vector | integer | logical vector

`Z0` — Presample disturbance paths z_t
numeric column vector | numeric matrix

`V0` — Positive presample conditional variance paths σ_t²
positive column vector | positive matrix

`Presample` — Presample data
table | timetable

`PresampleDisturbanceVariable` — Variable of `Presample` containing presample disturbance paths z_t
string scalar | character vector | integer | logical vector

`PresampleVarianceVariable` — Variable of `Presample` containing data for the presample conditional variances σ_t²
string scalar | character vector | integer | logical vector

`V` — Filtered conditional variance paths σ_t²
numeric column vector | numeric matrix

`Y` — Filtered response paths y_t
numeric column vector | numeric matrix

`Tbl2` — Filtered conditional variance σ_t² and response y_t paths
table | timetable

R2023a: `filter` accepts input data in tables and timetables, and returns results in tables and timetables