simulate

Monte Carlo simulation of univariate regression model with ARIMA time series errors

Syntax

Y = simulate(Mdl,numobs)

Y = simulate(Mdl,numobs,Name=Value)

[Y,E,U] = simulate(___)

Tbl = simulate(Mdl,numobs,Presample=Presample,PresampleInnovationVariable=PresampleInnovationVariable)

Tbl = simulate(Mdl,numobs,InSample=InSample,PredictorVariables=PredictorVariables)

Tbl = simulate(Mdl,numobs,Presample=Presample,PresampleInnovationVariable=PresampleInnovationVariable,InSample=InSample,PredictorVariables=PredictorVariables)

Tbl = simulate(___,Name=Value)

Description

Y = simulate(Mdl,numobs) returns the numeric vector Y containing a random numobs-period response path from simulating the fully specified regression model with ARIMA time series errors Mdl.

example

Y = simulate(Mdl,numobs,Name=Value) uses additional options specified by one or more name-value arguments. simulate returns numeric arrays when all optional input data are numeric arrays. For example, simulate(Mdl,10,NumPaths=1000,X=Pred) simulates 1000 sample paths of length 10 from the regression model with ARIMA errors Mdl, and uses the predictor data in Pred for the model regression component.

example

[Y,E,U] = simulate(___) uses any input-argument combination in the previous syntaxes to return numeric arrays of one or more independent series of error model innovations E and unconditional disturbances U, resulting from simulating the regression model with ARIMA errors.

example

Tbl = simulate(Mdl,numobs,Presample=Presample,PresampleInnovationVariable=PresampleInnovationVariable) returns the table or timetable Tbl containing a variable for each of the random paths of response, error model innovation, and unconditional disturbance series resulting from simulating the regression model with ARIMA errors Mdl. simulate uses the error model variable PresampleInnovationVariable in the table or timetable of presample data Presample to initialize the model. (since R2023b)

To initialize the model using presample unconditional disturbance data, replace the PresampleInnovationVariable name-value argument with PresampleRegressionDisturbanceVariable name-value argument.

example

Tbl = simulate(Mdl,numobs,InSample=InSample,PredictorVariables=PredictorVariables) specifies the variables PredictorVariables in the in-sample table or timetable of data InSample containing the predictor data for the model regression component. (since R2023b)

example

Tbl = simulate(Mdl,numobs,Presample=Presample,PresampleInnovationVariable=PresampleInnovationVariable,InSample=InSample,PredictorVariables=PredictorVariables) specifies presample error model innovation data to initialize the model and in-sample predictor data for the model regression component. (since R2023b)

example

Tbl = simulate(___,Name=Value) uses additional options specified by one or more name-value arguments, using any input argument combination in the previous three syntaxes. (since R2023b)

For example, simulate(Mdl,100,NumPaths=1000,InSample=Tbl,PredictoreVariables="CPI") returns a timetable containing a variable for each of the response, error model innovation, and unconditional disturbance series. Each variable is a 100-by-1000 matrix representing 1000, 100-period paths simulated from the regression model with ARIMA errors. simulate applies the predictor data in the CPI variable of the timetable Tbl to the model regression component.

example

Examples

collapse all

Simulate Response Path Vector From Regression Model with ARMA Errors

Open Live Script

Create the following regression model with ARMA(2,1) errors:

$\begin{array}{llllllllllllllllllll} \begin{array}{c} y_{t} = 1 + u_{t} \\ u_{t} = 0.5 u_{t - 1} - 0.8 u_{t - 2} + ε_{t} - 0.5 ε_{t - 1}, \end{array} \end{array}$

where $ε_{t}$ is Gaussian with variance 0.1.

Mdl = regARIMA(Intercept=1,AR={0.5 -0.8},MA=-0.5, ...
    Variance=0.1);

Mdl is a fully specified regARIMA object.

Simulate a path of responses of length 100.

rng(1,"twister")    % For reproducibility
y = simulate(Mdl,100);

y is a 100-by-1 vector containing the response path simulated from Mdl.

Plot the simulated path.

plot(y)

Figure contains an axes object. The axes object contains an object of type line.

Simulate Matrix of Response Paths

Open Live Script

Simulate 1000 paths of responses from the following regression model with ARMA(2,1) errors:

$\begin{array}{llllllllllllllllllll} \begin{array}{c} y_{t} = X_{t} [\begin{array}{cccccccccccccccccccc} 0.1 \\ - 0.2 \end{array}] + u_{t} \\ u_{t} = 0.5 u_{t - 1} - 0.8 u_{t - 2} + ε_{t} - 0.5 ε_{t - 1}, \end{array} \end{array}$

where $ε_{t}$ is Gaussian with variance 0.1. Assume the predictors are standard Gaussian random variables. Provide data as numeric arrays.

Create the regression model with ARIMA errors.

Mdl = regARIMA(Intercept=0,AR={0.5 -0.8},MA=-0.5, ...
    Beta=[0.1; -0.2],Variance=0.1);

Simulate two series of predictor data for the regression component.

rng(1,"twister")    % For reproducibility
Pred = randn(100,2);

Simulate 1000 paths of responses each of length 100.

numobs = 100;
numpaths = 1000;
y = simulate(Mdl,100,X=Pred,NumPaths=1000);

y is a 1000-by-100 matrix containing the independent response paths simulated from Mdl.

Plot the simulated paths.

plot(y)

Figure contains an axes object. The axes object contains 1000 objects of type line.

Simulate Responses, Innovations, and Unconditional Disturbances

Open Live Script

Simulate paths of responses, innovations, and unconditional disturbances from a regression model with SARIMA ${(2, 1, 1)}_{12}$ errors.

Specify the model:

$\begin{array}{c} y_{t} = X [\begin{array}{cccccccccccccccccccc} 1.5 \\ - 2 \end{array}] + u_{t} \\ (1 - 0.2 L - 0.1 L^{2}) (1 - L) (1 - 0.01 L^{12}) (1 - L^{12}) u_{t} = (1 + 0.5 L) (1 + 0.02 L^{12}) ε_{t}, \end{array}$

where $ε_{t}$ follows a t-distribution with 15 degrees of freedom.

dstr = struct("Name","t","DoF",15);
Mdl = regARIMA(AR={0.2 0.1},MA=0.5,SAR=0.01,SARLags=12, ...
    SMA=0.02,SMALags=12,D=1,Seasonality=12,Beta=[1.5; -2], ...
    Intercept=0,Variance=0.1,Distribution=dstr)

Mdl = 
  regARIMA with properties:

     Description: "Regression with ARIMA(2,1,1) Error Model Seasonally Integrated with Seasonal AR(12) and MA(12) (t Distribution)"
      SeriesName: "Y"
    Distribution: Name = "t", DoF = 15
       Intercept: 0
            Beta: [1.5 -2]
               P: 27
               D: 1
               Q: 13
              AR: {0.2 0.1} at lags [1 2]
             SAR: {0.01} at lag [12]
              MA: {0.5} at lag [1]
             SMA: {0.02} at lag [12]
     Seasonality: 12
        Variance: 0.1

Simulate and plot 500 paths with 25 observations each.

T = 25;
rng(1,"twister") % For reproducibility
Pred = randn(T,2);
[Y,E,U] = simulate(Mdl,T,NumPaths=500,X=Pred);

figure
tiledlayout(3,1)
nexttile
plot(Y)
axis tight
title("Simulated Response Paths")
nexttile
plot(E)
axis tight
title("Simulated Innovations Paths")
nexttile
plot(U)
axis tight
title("Simulated Unconditional Disturbances Paths")

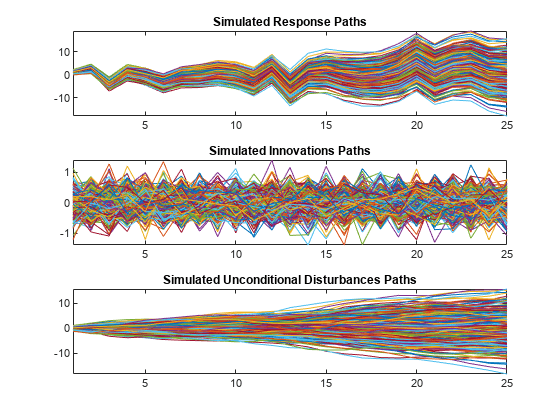
Figure contains 3 axes objects. Axes object 1 with title Simulated Response Paths contains 500 objects of type line. Axes object 2 with title Simulated Innovations Paths contains 500 objects of type line. Axes object 3 with title Simulated Unconditional Disturbances Paths contains 500 objects of type line.

Plot the 2.5th, 50th (median), and 97.5th percentiles of the simulated response paths.

lower = prctile(Y,2.5,2);
middle = median(Y,2);
upper = prctile(Y,97.5,2);

figure
plot(1:25,lower,"r:",1:25,middle,"k",1:25,upper,"r:")
title("95% Percentile Confidence Interval for Response")
legend("95% Interval","Median",Location="best")

Figure contains an axes object. The axes object with title 95% Percentile Confidence Interval for Response contains 3 objects of type line. These objects represent 95% Interval, Median.

Compute statistics across the second dimension (across paths) to summarize the sample paths.

Plot a histogram of the simulated paths at time 20.

figure
histogram(Y(20,:),10)
title("Response Distribution at Time 20")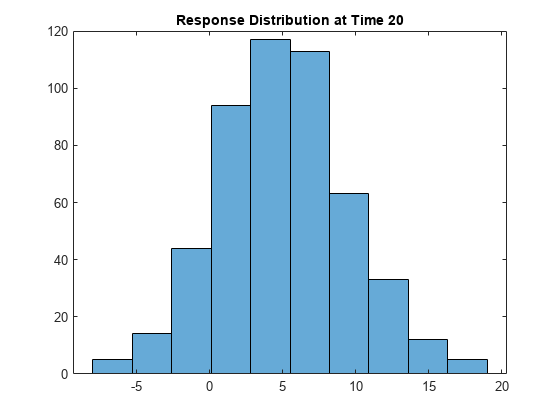

Figure contains an axes object. The axes object with title Response Distribution at Time 20 contains an object of type histogram.

Forecast Model With Stationary Errors Using Monte Carlo Simulations

Open Live Script

Fit a regression model with ARMA(1,1) errors by regressing the US consumer price index (CPI) quarterly changes onto the US gross domestic product (GDP) growth rate. Forecast log GDP using Monte Carlo simulation and the estimated model. Supply data in timetables.

Load and Transform Data

Load the US macroeconomic data set. Compute the series of GDP quarterly growth rates and CPI quarterly changes.

load Data_USEconModel
DTT = price2ret(DataTimeTable,DataVariables="GDP");
DTT.GDPRate = 100*DTT.GDP;
DTT.CPIDel = diff(DataTimeTable.CPIAUCSL);
T = height(DTT)

T = 
248

figure
tiledlayout(2,1)
nexttile
plot(DTT.Time,DTT.GDPRate)
title("GDP Rate")
ylabel("Percent Growth")
nexttile
plot(DTT.Time,DTT.CPIDel)
title("Index")

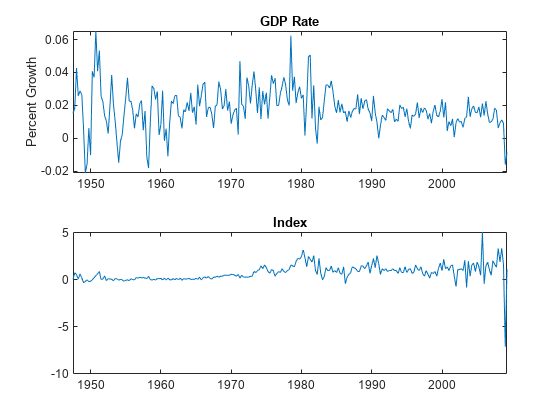
Figure contains 2 axes objects. Axes object 1 with title GDP Rate, ylabel Percent Growth contains an object of type line. Axes object 2 with title Index contains an object of type line.

The series appear stationary, albeit heteroscedastic.

Prepare Timetable for Estimation

When you plan to supply a timetable, you must ensure it has all the following characteristics:

The selected response variable is numeric and does not contain any missing values.
The timestamps in the Time variable are regular, and they are ascending or descending.

Remove all missing values from the timetable.

DTT = rmmissing(DTT);
T_DTT = height(DTT)

T_DTT = 
248

Because each sample time has an observation for all variables, rmmissing does not remove any observations.

Determine whether the sampling timestamps have a regular frequency and are sorted.

areTimestampsRegular = isregular(DTT,"quarters")

areTimestampsRegular = logical
   0

areTimestampsSorted = issorted(DTT.Time)

areTimestampsSorted = logical
   1

areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.

Remedy the time irregularity by shifting all dates to the first day of the quarter.

dt = DTT.Time;
dt = dateshift(dt,"start","quarter");
DTT.Time = dt;
areTimestampsRegular = isregular(DTT,"quarters")

areTimestampsRegular = logical
   1

DTT is regular.

Create Model Template for Estimation

Suppose that a regression model of the quarterly GDP rate on CPI changes, with ARMA(1,1) errors, is appropriate.

Create a model template for a regression model with ARMA(1,1) errors template. Specify the response variable name.

Mdl = regARIMA(1,0,1);
Mdl.SeriesName = "GDPRate";

Mdl is a partially specified regARIMA object.

Partition Data

Reserve 2 years (8 quarters) of data at the end of the series to compare against the forecasts.

numobs = 8;
estidx = 1:(T_DTT-numobs);          % Estimation sample 
frstHzn = (T_DTT-numobs+1):T_DTT;   % Forecast horizon

Fit Model to Data

Fit a regression model with ARMA(1,1) errors to the estimation sample. Specify the predictor variable name.

EstMdl = estimate(Mdl,DTT(estidx,:),PredictorVariables="CPIDel");

 
    Regression with ARMA(1,1) Error Model (Gaussian Distribution):
 
                   Value       StandardError    TStatistic      PValue  
                 __________    _____________    __________    __________

    Intercept      0.016489      0.0017307        9.5272      1.6152e-21
    AR{1}           0.57835       0.096952        5.9653      2.4415e-09
    MA{1}          -0.15125        0.11658       -1.2974         0.19449
    Beta(1)       0.0025095      0.0014147        1.7738        0.076089
    Variance     0.00011319     7.5405e-06         15.01      6.2792e-51

EstMdl is a fully specified, estimated regARIMA object. By default, estimate backcasts for the required Mdl.P = 1 presample regression model residual and sets the required Mdl.Q = 1 presample error model residual to 0.

Forecast Estimated Model

Infer estimation sample unconditional disturbances to initialize the model for forecasting. Specify the predictor variable name.

Tbl0 = infer(EstMdl,DTT(estidx,:),PredictorVariables="CPIDel");

Simulate 1000 paths with 8 observations each. Use the inferred unconditional disturbances as presample data. Specify the predictor and presample unconditional disturbance variable names.

rng(1,"twister");   % For reproducibility
numpaths = 1000;
TblSim = simulate(EstMdl,numobs,NumPaths=numpaths,Presample=Tbl0, ...
   PresampleRegressionDisturbanceVariable="GDPRate_RegressionResidual", ...
   InSample=DTT(frstHzn,:),PredictorVariables="CPIDel");

Plot the simulation median forecast and approximate 95% forecast intervals.

TblSim.FStats = quantile(TblSim.GDPRate_Response,[0.025 0.5 0.975],2);
figure
plot(DTT.Time(end-40:end),DTT.GDPRate(end-40:end),Color=[.7,.7,.7])
hold on
h1 = plot(TblSim.Time,TblSim.FStats(:,[1 3]),"r:",LineWidth=2);
h2 = plot(TblSim.Time,TblSim.FStats(:,2),"k",LineWidth=2);
h = gca;
ph = patch([repmat(TblSim.Time(1),1,2) repmat(TblSim.Time(end),1,2)], ...
   [h.YLim fliplr(h.YLim)], ...
   [0 0 0 0],"b");
ph.FaceAlpha = 0.1;
legend([h1(1) h2],["95% percentile intervals" "Sim. median"],Location="northwest", ...
    AutoUpdate="off")
axis tight
title("GDP Rate Forecast Over 2-year Horizon")
hold off

Figure contains an axes object. The axes object with title GDP Rate Forecast Over 2-year Horizon contains 5 objects of type line, patch. These objects represent 95% percentile intervals, Sim. median.

Forecast Model with Nonstationary Errors Using Monte Carlo Simulation

Open Live Script

Fit a regression model with ARIMA(1,1,1) errors by regressing the quarterly log US GDP onto the log CPI. Forecast log GDP using Monte Carlo simulation and the estimated model. Supply data in timetables.

Load the US macroeconomic data set. Compute the log GDP series.

load Data_USEconModel
DTT = DataTimeTable;
DTT.LogGDP = log(DTT.GDP);
T = height(DTT);

Remedy the time irregularity by shifting all dates to the first day of the quarter.

dt = DTT.Time;
dt = dateshift(dt,"start","quarter");
DTT.Time = dt;

Reserve 2 years (8 quarters) of data at the end of the series to compare against the forecasts.

numobs = 8;
estidx = 1:(T-numobs);     % Estimation sample 
frstHzn = (T-numobs+1):T;  % Forecast horizon

Suppose that a regression model of the quarterly log GDP on CPI, with ARMA(1,1) errors, is appropriate.

Create a model template for a regression model with ARMA(1,1) errors template. Specify the response variable name.

Mdl = regARIMA(1,1,1);
Mdl.SeriesName = "LogGDP";

The intercept is not identifiable in a regression model with integrated errors. Fix its value before estimation. One way to do this is to estimate the intercept using simple linear regression. Use the estimation sample.

coeff = [ones(T-numobs,1) DTT.CPIAUCSL(estidx)]\DTT.LogGDP(estidx);
Mdl.Intercept = coeff(1);

Fit a regression model with ARMA(1,1,1) errors to the estimation sample. Specify the predictor variable name.

EstMdl = estimate(Mdl,DTT(estidx,:),PredictorVariables="CPIAUCSL");

 
    Regression with ARIMA(1,1,1) Error Model (Gaussian Distribution):
 
                   Value       StandardError    TStatistic      PValue   
                 __________    _____________    __________    ___________

    Intercept        5.8303              0           Inf                0
    AR{1}           0.92869       0.028414        32.684      2.6126e-234
    MA{1}          -0.39063       0.057599       -6.7819       1.1858e-11
    Beta(1)       0.0029335      0.0014645        2.0031         0.045166
    Variance     0.00010668     6.9256e-06        15.403        1.554e-53

EstMdl is a fully specified, estimated regARIMA object. By default, estimate backcasts for the required Mdl.P = 2 presample regression model residual and sets the required Mdl.Q = 1 presample error model residual to 0.

Infer estimation sample unconditional disturbances to initialize the model for forecasting. Specify the predictor variable name.

Tbl0 = infer(EstMdl,DTT(estidx,:),PredictorVariables="CPIAUCSL");

Simulate 1000 paths with 8 observations each. Use the inferred unconditional disturbances as presample data. Specify the predictor and presample unconditional disturbance variable names.

rng(1,"twister");   % For reproducibility
numpaths = 1000;
TblSim = simulate(EstMdl,numobs,NumPaths=numpaths,Presample=Tbl0, ...
   PresampleRegressionDisturbanceVariable="LogGDP_RegressionResidual", ...
   InSample=DTT(frstHzn,:),PredictorVariables="CPIAUCSL");

Plot the simulation median forecast and approximate 95% forecast intervals.

TblSim.FStats = quantile(TblSim.LogGDP_Response,[0.025 0.5 0.975],2);
figure
plot(DTT.Time(end-40:end),DTT.LogGDP(end-40:end),Color=[.7,.7,.7])
hold on
h1 = plot(TblSim.Time,TblSim.FStats(:,[1 3]),"r:",LineWidth=2);
h2 = plot(TblSim.Time,TblSim.FStats(:,2),"k",LineWidth=2);
h = gca;
ph = patch([repmat(TblSim.Time(1),1,2) repmat(TblSim.Time(end),1,2)], ...
   [h.YLim fliplr(h.YLim)],[0 0 0 0],"b");
ph.FaceAlpha = 0.1;
legend([h1(1) h2],["95% percentile intervals" "Sim. median"],Location="northwest", ...
    AutoUpdate="off")
axis tight
title("Log GDP Forecast Over 2-year Horizon")
hold off

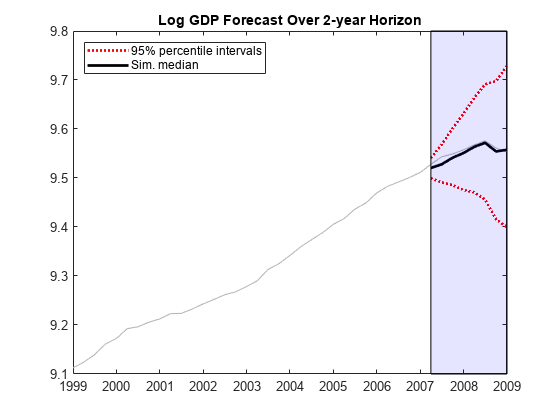
Figure contains an axes object. The axes object with title Log GDP Forecast Over 2-year Horizon contains 5 objects of type line, patch. These objects represent 95% percentile intervals, Sim. median.

Input Arguments

collapse all

`Mdl` — Fully specified regression model with ARIMA errors
`regARIMA` model object

Fully specified regression model with ARIMA errors, specified as a regARIMA model object created by regARIMA or estimate.

The properties of Mdl cannot contain NaN values.

`numobs` — Number of random observations to generate
positive integer

Sample path length, specified as a positive integer. numobs is the number of random observations to generate per output path.

Data Types: double

`Presample` — Presample data
table | timetable

Since R2023b

Presample data containing paths of responses error model innovations ε_t or unconditional disturbances u_t to initialize the model, specified as a table or timetable with numprevars variables and numpreobs rows.

simulate returns the simulated variables in the output table or timetable Tbl, which is the same type as Presample. If Presample is a timetable, Tbl is a timetable that immediately follows Presample in time with respect to the sampling frequency.

Each selected variable is a single path (numpreobs-by-1 vector) or multiple paths (numpreobs-by-numprepaths matrix) of numpreobs observations representing the presample of numpreobs observations of error model innovations or unconditional disturbances.

Each row is a presample observation, and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be one of the following values:

At least Mdl.P when Presample provides only presample unconditional disturbances
At least Mdl.Q when Presample provides only presample error model innovations
At least max([Mdl.P Mdl.Q]) otherwise

If numpreobs exceeds the minimum number, simulate uses the latest required number of observations only.

If numprepaths > NumPaths, simulate uses only the first NumPaths columns.

If Presample is a timetable, all the following conditions must be true:

Presample must represent a sample with a regular datetime time step (see isregular).
The datetime vector of sample timestamps Presample.Time must be ascending or descending.
If you specify InSample, Presample must immediately precede InSample, with respect to the sampling frequency.

If Presample is a table, the last row contains the latest presample observation.

By default, simulate sets necessary presample error model innovations and unconditional disturbances to zero.

If you specify the Presample, you must specify the presample error model innovation or unconditional disturbance variable name by using the PresampleInnovationVariable or PresampleRegressionDisturbanceVariable name-value argument.

`PresampleInnovationVariable` — Error model innovation ε_t to select from `Presample`
string scalar | character vector | integer | logical vector

Since R2023b

Error model innovation ε_t to select from Presample containing the presample error model innovation data, specified as one of the following data types:

String scalar or character vector containing the variable name to select from Presample.Properties.VariableNames
Variable index (positive integer) to select from Presample.Properties.VariableNames
A logical vector, where PresampleInnovationVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaNs).

If you specify presample error model innovation data by using the Presample name-value argument, you must specify PresampleInnovationVariable.

Example: PresampleInnovationVariable="GDP_E"

Example: PresampleInnovationVariable=[false false true false] or PresampleInnovationVariable=3 selects the third table variable for presample error model innovation data.

Data Types: double | logical | char | cell | string

`InSample` — In-sample predictor data
table | timetable

Since R2023b

In-sample predictor data for the model regression component, specified as a table or timetable. InSample contains numvars variables, including numpreds predictor variables x_t.

simulate returns the simulated variables in the output table or timetable Tbl, which is commensurate with InSample.

Each row corresponds to an observation in the simulation horizon, the first row is the earliest observation, and measurements in each row, among all paths, occur simultaneously. InSample must have at least numobs rows to cover the simulation horizon. If you supply more rows than necessary, simulate uses only the first numobs rows.

Each selected predictor variable is a numeric vector without missing values (NaNs). All predictor variables are present in the regression component of each response equation and apply to all response paths.

If InSample is a timetable, the following conditions apply:

InSample must represent a sample with a regular datetime time step (see isregular).
The datetime vector InSample.Time must be ascending or descending.
If you specify Presample, Presample must immediately precede InSample, with respect to the sampling frequency.

If InSample is a table, the last row contains the latest observation.

By default, simulate does not include the regression component in the model, regardless of the value of Mdl.Beta.

`PredictorVariables` — Predictor variables x_t to select from `InSample`
string vector | cell vector of character vectors | vector of integers | logical vector

Predictor variables x_t to select from InSample containing predictor data for the regression component, specified as one of the following data types:

String vector or cell vector of character vectors containing numpreds variable names in InSample.Properties.VariableNames
A vector of unique indices (positive integers) of variables to select from InSample.Properties.VariableNames
A logical vector, where PredictorVariables(j) = true selects variable j from InSample.Properties.VariableNames

The selected variables must be numeric vectors and cannot contain missing values (NaNs).

By default, simulate excludes the regression component, regardless of its presence in Mdl.

Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]

Example: PredictorVariables=[true false true false] or PredictorVariable=[1 3] selects the first and third table variables to supply the predictor data.

Data Types: double | logical | char | cell | string

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: simulate(Mdl,100,NumPaths=1000,InSample=Tbl,PredictoreVariables="CPI") returns a timetable containing a variable for each of the response, error model innovation, and unconditional disturbance series. Each variable is a 100-by-1000 matrix representing 1000, 100-period paths simulated from the regression model with ARIMA errors. simulate applies the predictor data in the CPI variable of the timetable Tbl to the model regression component.

`NumPaths` — Number of independent sample paths to generate
`1` (default) | positive integer

Number of independent sample paths to generate, specified as a positive integer.

Example: NumPaths=1000

Data Types: double

`X` — Predictor data
numeric matrix

Predictor data for the model regression component, specified as a numeric matrix containing numpreds columns. numpreds is the number of predictor variables (numel(Mdl.Beta)). Use X only when you supply optional data inputs as numeric arrays.

Each row of X corresponds to a period in the length numobs simulation sample (period for which simulate simulates observations; the period after the presample). X must have at least numobs rows. The last row contains the latest predictor data. If X has more than numobs rows, simulate uses only the latest numobs rows.

simulate does not use the regression component in the presample period.

Each column is an individual predictor variable.

simulate applies X to each path; that is, X represents one path of observed predictors.

By default, simulate excludes the regression component, regardless of its presence in Mdl.

Data Types: double

`E0` — Presample error model innovations ε_t
`0` (default) | numeric column vector | numeric matrix

Presample error model innovations ε_t used to initialize the moving average (MA) component of the error model, specified as a numpreobs-by-1 numeric column vector or a numpreobs-by-numprepaths matrix. Use E0 only when you supply optional data inputs as numeric arrays.

numpreobs is the number of presample observations. numprepaths is the number of presample response paths.

Each row is a presample observation (sampling time), and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.Q to initialize the MA component. If numpreobs is larger than required, simulate uses the latest required number of observations only.

Columns of E0 are separate, independent presample paths. The following conditions apply:

If E0 is a column vector, it represents a single residual path. simulate applies it to each output path.
If E0 is a matrix, simulate applies E0(:,j) to initialize simulating path j. E0 must have at least NumPaths columns; simulate uses only the first NumPaths columns of E0.

Data Types: double

`U0` — Presample unconditional disturbances u_t
`0` (default) | numeric column vector | numeric matrix

Presample unconditional disturbances u_t used to initialize the autoregressive (AR) component of the error model, specified as a numpreobs-by-1 numeric column vector or a numpreobs-by-numprepaths matrix. Use U0 only when you supply optional data inputs as numeric arrays.

Each row is a presample observation (sampling time), and measurements in each row occur simultaneously. The last row contains the latest presample observation. numpreobs must be at least Mdl.P to initialize the AR component. If numpreobs is larger than required, simulate uses the latest required number of observations only.

Columns of U0 are separate, independent presample paths. The following conditions apply:

If U0 is a column vector, it represents a single residual path. simulate applies it to each output path.
If U0 is a matrix, simulate applies U0(:,j) to initialize simulating path j. U0 must have at least NumPaths columns; simulate uses only the first NumPaths columns of U0.

Data Types: double

`PresampleRegressionDistrubanceVariable` — Unconditional disturbance variable u_t to select from `Presample`
string scalar | character vector | integer | logical vector

Since R2023b

Unconditional disturbance variable u_t to select from Presample containing data for the presample unconditional disturbances, specified as one of the following data types:

String scalar or character vector containing a variable name in Presample.Properties.VariableNames
Variable index (positive integer) to select from Presample.Properties.VariableNames
A logical vector, where PresampleRegressionDistrubanceVariable(j) = true selects variable j from Presample.Properties.VariableNames

The selected variable must be a numeric vector and cannot contain missing values (NaNs).

If you specify presample unconditional disturbance data by using the Presample name-value argument, you must specify PresampleRegressionDistrubanceVariable.

Example: PresampleRegressionDistrubanceVariable="StockRateU"

Example: PresampleRegressionDistrubanceVariable=[false false true false] or PresampleRegressionDistrubanceVariable=3 selects the third table variable as the presample unconditional disturbance data.

Data Types: double | logical | char | cell | string

Note

NaN values in X, E0, and U0 indicate missing values. simulate removes missing values from specified data by list-wise deletion.
- For the presample, simulate horizontally concatenates the possibly jagged arrays E0 and U0 with respect to the last rows, and then it removes any row of the concatenated matrix containing at least one NaN.
- For in-sample data, simulate removes any row of X containing at least one NaN.
This type of data reduction reduces the effective sample size and can create an irregular time series.
For numeric data inputs, simulate assumes that you synchronize the presample data such that the latest observations occur simultaneously.
simulate issues an error when any table or timetable input contains missing values.

Output Arguments

collapse all

`Y` — Simulated response paths y_t
numeric column vector | numeric matrix

Simulated response paths y_t, returned as a numobs-by-1 numeric column vector or a numobs-by-NumPaths numeric matrix. simulate returns Y by default and when you supply optional data in numeric arrays.

Y represents the continuation of the presample responses in Y0.

Each row corresponds to a period in the simulated series; the simulated series has the periodicity of Mdl. Each column is a separate simulated path.

`E` — Simulated error model innovation paths ε_t
numeric column vector | numeric matrix

Simulated error model innovations paths ε_t, returned as a numobs-by-1 numeric column vector or a numobs-by-NumPaths numeric matrix. Each column (path) of E has a mean of zero. simulate returns E by default and when you supply optional data in numeric arrays

The dimensions of E correspond to the dimensions of Y.

`U` — Simulated unconditional disturbance paths u_t
numeric column vector | numeric matrix

Simulated unconditional disturbance paths u_t, returned as a numobs-by-1 numeric column vector or a numobs-by-NumPaths numeric matrix.

The dimensions of U correspond to the dimensions of Y.

`Tbl` — Simulated response y_t, error model innovation ε_t, and unconditional disturbance u_t paths
table | timetable

Since R2023b

Simulated response y_t, error model innovation ε_t, and unconditional disturbance u_t paths, returned as a table or timetable, the same data type as Presample or InSample. simulate returns Tbl only when you supply at least one of the inputs Presample and InSample.

Tbl contains the following variables:

The simulated response paths, which are in a numobs-by-NumPaths numeric matrix, with rows representing observations and columns representing independent paths. Each path represents the continuation of the presample in Presample, or each path corresponds, in time, with the rows of InSample. simulate names the simulated response variable in Tbl responseName_Response, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is GDP, Tbl contains a variable for the corresponding simulated response paths with the name GDP_Response.
The simulated error model innovation paths, which are in a numobs-by-NumPaths numeric matrix, with rows representing observations and columns representing independent paths. Each path has a mean of zero, and represents the continuation of the corresponding presample path in Presample, or each path corresponds, in time, with the rows of InSample. simulate names the simulated error model innovation variable in Tbl responseName_ErrorInnovation, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is GDP, Tbl contains a variable for the corresponding simulated error model innovation paths with the name GDP_ErrorInnovation.
The simulated unconditional disturbance paths, which are in a numobs-by-NumPaths numeric matrix, with rows representing observations and columns representing independent paths. Each path represents the continuation of the corresponding presample path in Presample, or each path corresponds, in time, with the rows of InSample. simulate names the simulated unconditional disturbance variable in Tbl responseName_RegressionInnovation, where responseName is Mdl.SeriesName. For example, if Mdl.SeriesName is GDP, Tbl contains a variable for the corresponding simulated unconditional disturbance paths with the name GDP_RegressionInnovation.
When you supply InSample, Tbl contains all variables in InSample.

If Tbl is a timetable, the following conditions hold:

The row order of Tbl, either ascending or descending, matches the row order of Preample.
If you specify InSample, row times Tbl.Time are InSample.Time(1:numobs). Otherwise, Tbl.Time(1) is the next time after Presample(end) relative to the sampling frequency, and Tbl.Time(2:numobs) are the following times relative to the sampling frequency.

References

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.

[2] Davidson, R., and J. G. MacKinnon. Econometric Theory and Methods. Oxford, UK: Oxford University Press, 2004.

[3] Enders, Walter. Applied Econometric Time Series. Hoboken, NJ: John Wiley & Sons, Inc., 1995.

[4] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.

[5] Pankratz, A. Forecasting with Dynamic Regression Models. John Wiley & Sons, Inc., 1991.

[6] Tsay, R. S. Analysis of Financial Time Series. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc., 2005.

Version History

Introduced in R2013b

expand all

R2023a: `simulate` accepts input data in tables and timetables, and returns results in tables and timetables

In addition to accepting presample and in-sample predictor data in numeric arrays, simulate accepts input data in tables or regular timetables. When you supply input data in a table or timetable, the following conditions apply:

If you specify optional presample error model innovation or unconditional disturbance data to initialize the model, you must also specify corresponding variable names containing the data to use.
If you specify optional in-sample predictor data for the model regression component, you must also specify corresponding predictor variable names containing the data to use.
simulate returns results in a table or timetable.

Name-value arguments to support tabular workflows include:

InSample specifies the table or regular timetable of predictor data for the model regression component.
PredictorVariables specifies the names of the predictor series to select from InSample for the model regression component.
Presample specifies the input table or timetable of presample regression innovation or error model innovation data.
PresampleInnovationVariable specifies the name of the error model innovation series to select from Presample.
PresampleRegressionDisturbanceVariable specifies the name of the unconditional disturbance series to select from Presample.

simulate

Syntax

Description

Examples

Simulate Response Path Vector From Regression Model with ARMA Errors

Simulate Matrix of Response Paths

Simulate Responses, Innovations, and Unconditional Disturbances

Forecast Model With Stationary Errors Using Monte Carlo Simulations

Forecast Model with Nonstationary Errors Using Monte Carlo Simulation

Input Arguments

`Mdl` — Fully specified regression model with ARIMA errors
`regARIMA` model object

`numobs` — Number of random observations to generate
positive integer

`Presample` — Presample data
table | timetable

`PresampleInnovationVariable` — Error model innovation ε_t to select from `Presample`
string scalar | character vector | integer | logical vector

`InSample` — In-sample predictor data
table | timetable

`PredictorVariables` — Predictor variables x_t to select from `InSample`
string vector | cell vector of character vectors | vector of integers | logical vector

Name-Value Arguments

`NumPaths` — Number of independent sample paths to generate
`1` (default) | positive integer

`X` — Predictor data
numeric matrix

`E0` — Presample error model innovations ε_t
`0` (default) | numeric column vector | numeric matrix

`U0` — Presample unconditional disturbances u_t
`0` (default) | numeric column vector | numeric matrix

`PresampleRegressionDistrubanceVariable` — Unconditional disturbance variable u_t to select from `Presample`
string scalar | character vector | integer | logical vector

Output Arguments

`Y` — Simulated response paths y_t
numeric column vector | numeric matrix

`E` — Simulated error model innovation paths ε_t
numeric column vector | numeric matrix

`U` — Simulated unconditional disturbance paths u_t
numeric column vector | numeric matrix

`Tbl` — Simulated response y_t, error model innovation ε_t, and unconditional disturbance u_t paths
table | timetable

References

Version History

R2023a: `simulate` accepts input data in tables and timetables, and returns results in tables and timetables

See Also

Objects

Functions

Topics

simulate

Syntax

Description

Examples

Simulate Response Path Vector From Regression Model with ARMA Errors

Simulate Matrix of Response Paths

Simulate Responses, Innovations, and Unconditional Disturbances

Forecast Model With Stationary Errors Using Monte Carlo Simulations

Forecast Model with Nonstationary Errors Using Monte Carlo Simulation

Input Arguments

Mdl — Fully specified regression model with ARIMA errors regARIMA model object

numobs — Number of random observations to generate positive integer

Presample — Presample data table | timetable

PresampleInnovationVariable — Error model innovation εt to select from Presample string scalar | character vector | integer | logical vector

InSample — In-sample predictor data table | timetable

PredictorVariables — Predictor variables xt to select from InSample string vector | cell vector of character vectors | vector of integers | logical vector

Name-Value Arguments

NumPaths — Number of independent sample paths to generate 1 (default) | positive integer

X — Predictor data numeric matrix

E0 — Presample error model innovations εt 0 (default) | numeric column vector | numeric matrix

U0 — Presample unconditional disturbances ut 0 (default) | numeric column vector | numeric matrix

PresampleRegressionDistrubanceVariable — Unconditional disturbance variable ut to select from Presample string scalar | character vector | integer | logical vector

Output Arguments

Y — Simulated response paths yt numeric column vector | numeric matrix

E — Simulated error model innovation paths εt numeric column vector | numeric matrix

U — Simulated unconditional disturbance paths ut numeric column vector | numeric matrix

Tbl — Simulated response yt, error model innovation εt, and unconditional disturbance ut paths table | timetable

References

Version History

R2023a: simulate accepts input data in tables and timetables, and returns results in tables and timetables

See Also

Objects

Functions

Topics

`Mdl` — Fully specified regression model with ARIMA errors
`regARIMA` model object

`numobs` — Number of random observations to generate
positive integer

`Presample` — Presample data
table | timetable

`PresampleInnovationVariable` — Error model innovation ε_t to select from `Presample`
string scalar | character vector | integer | logical vector

`InSample` — In-sample predictor data
table | timetable

`PredictorVariables` — Predictor variables x_t to select from `InSample`
string vector | cell vector of character vectors | vector of integers | logical vector

`NumPaths` — Number of independent sample paths to generate
`1` (default) | positive integer

`X` — Predictor data
numeric matrix

`E0` — Presample error model innovations ε_t
`0` (default) | numeric column vector | numeric matrix

`U0` — Presample unconditional disturbances u_t
`0` (default) | numeric column vector | numeric matrix

`PresampleRegressionDistrubanceVariable` — Unconditional disturbance variable u_t to select from `Presample`
string scalar | character vector | integer | logical vector

`Y` — Simulated response paths y_t
numeric column vector | numeric matrix

`E` — Simulated error model innovation paths ε_t
numeric column vector | numeric matrix

`U` — Simulated unconditional disturbance paths u_t
numeric column vector | numeric matrix

`Tbl` — Simulated response y_t, error model innovation ε_t, and unconditional disturbance u_t paths
table | timetable

R2023a: `simulate` accepts input data in tables and timetables, and returns results in tables and timetables