forecast

Forecast states and observations of state-space models

Syntax

[Y,YMSE]
= forecast(Mdl,numPeriods,Y0)

[Y,YMSE]
= forecast(Mdl,numPeriods,Y0,Name,Value)

[Y,YMSE,X,XMSE]
= forecast(___)

Description

[Y,YMSE] = forecast(Mdl,numPeriods,Y0) returns forecasted observations (Y) and their corresponding variances (YMSE) from forecasting the state-space model Mdl using a numPeriods forecast horizon and in-sample observations Y0.

example

[Y,YMSE] = forecast(Mdl,numPeriods,Y0,Name,Value) uses additional options specified by one or more Name,Value pair arguments. For example, for state-space models that include a linear regression component in the observation model, include in-sample predictor data, predictor data for the forecast horizon, and the regression coefficient.

example

[Y,YMSE,X,XMSE] = forecast(___) uses any of the input arguments in the previous syntaxes to additionally return state forecasts (X) and their corresponding variances (XMSE).

example

Examples

collapse all

Forecast Observations of Time-Invariant State-Space Model

Open Live Script

Suppose that a latent process is an AR(1). The state equation is

$x_{t} = 0.5 x_{t - 1} + u_{t},$

where $u_{t}$ is Gaussian with mean 0 and standard deviation 1.

Generate a random series of 100 observations from $x_{t}$ , assuming that the series starts at 1.5.

T = 100;
ARMdl = arima('AR',0.5,'Constant',0,'Variance',1);
x0 = 1.5;
rng(1); % For reproducibility
x = simulate(ARMdl,T,'Y0',x0);

Suppose further that the latent process is subject to additive measurement error. The observation equation is

$y_{t} = x_{t} + ε_{t},$

where $ε_{t}$ is Gaussian with mean 0 and standard deviation 0.75. Together, the latent process and observation equations compose a state-space model.

Use the random latent state process (x) and the observation equation to generate observations.

y = x + 0.75*randn(T,1);

Specify the four coefficient matrices.

A = 0.5;
B = 1;
C = 1;
D = 0.75;

Specify the state-space model using the coefficient matrices.

Mdl = ssm(A,B,C,D)

Mdl = 
State-space model type: ssm

State vector length: 1
Observation vector length: 1
State disturbance vector length: 1
Observation innovation vector length: 1
Sample size supported by model: Unlimited

State variables: x1, x2,...
State disturbances: u1, u2,...
Observation series: y1, y2,...
Observation innovations: e1, e2,...

State equation:
x1(t) = (0.50)x1(t-1) + u1(t)

Observation equation:
y1(t) = x1(t) + (0.75)e1(t)

Initial state distribution:

Initial state means
 x1 
  0 

Initial state covariance matrix
     x1   
 x1  1.33 

State types
     x1     
 Stationary

Mdl is an ssm model. Verify that the model is correctly specified using the display in the Command Window. The software infers that the state process is stationary. Subsequently, the software sets the initial state mean and covariance to the mean and variance of the stationary distribution of an AR(1) model.

Forecast the observations 10 periods into the future, and estimate their variances.

numPeriods = 10;
[ForecastedY,YMSE] = forecast(Mdl,numPeriods,y);

Plot the forecasts with the in-sample responses, and 95% Wald-type forecast intervals.

ForecastIntervals(:,1) = ForecastedY - 1.96*sqrt(YMSE);
ForecastIntervals(:,2) = ForecastedY + 1.96*sqrt(YMSE);

figure
plot(T-20:T,y(T-20:T),'-k',T+1:T+numPeriods,ForecastedY,'-.r',...
    T+1:T+numPeriods,ForecastIntervals,'-.b',...
    T:T+1,[y(end)*ones(3,1),[ForecastedY(1);ForecastIntervals(1,:)']],':k',...
    'LineWidth',2)
hold on
title({'Observed Responses and Their Forecasts'})
xlabel('Period')
ylabel('Responses')
legend({'Observations','Forecasted observations','95% forecast intervals'},...
    'Location','Best')
hold off

Figure contains an axes object. The axes object with title Observed Responses and Their Forecasts, xlabel Period, ylabel Responses contains 7 objects of type line. These objects represent Observations, Forecasted observations, 95% forecast intervals.

Forecast Observations of State-Space Model Containing Regression Component

Open Live Script

Suppose that the linear relationship between the change in the unemployment rate and the nominal gross national product (nGNP) growth rate is of interest. Suppose further that the first difference of the unemployment rate is an ARMA(1,1) series. Symbolically, and in state-space form, the model is

$\begin{array}{l} [\begin{array}{cccccccccccccccccccc} x_{1, t} \\ x_{2, t} \end{array}] = [\begin{array}{cccccccccccccccccccc} ϕ & θ \\ 0 & 0 \end{array}] [\begin{array}{cccccccccccccccccccc} x_{1, t - 1} \\ x_{2, t - 1} \end{array}] + [\begin{array}{cccccccccccccccccccc} 1 \\ 1 \end{array}] u_{1, t} \\ y_{t} - β Z_{t} = x_{1, t} + σ ε_{t}, \end{array}$

where:

$x_{1, t}$ is the change in the unemployment rate at time t.
$x_{2, t}$ is a dummy state for the MA(1) effect.
$y_{1, t}$ is the observed change in the unemployment rate being deflated by the growth rate of nGNP ( $Z_{t}$ ).
$u_{1, t}$ is the Gaussian series of state disturbances having mean 0 and standard deviation 1.
$ε_{t}$ is the Gaussian series of observation innovations having mean 0 and standard deviation $σ$ .

Load the Nelson-Plosser data set, which contains the unemployment rate and nGNP series, among other things.

load Data_NelsonPlosser

Preprocess the data by taking the natural logarithm of the nGNP series, and the first difference of each series. Also, remove the starting NaN values from each series.

isNaN = any(ismissing(DataTable),2);       % Flag periods containing NaNs
gnpn = DataTable.GNPN(~isNaN);
u = DataTable.UR(~isNaN);
T = size(gnpn,1);                          % Sample size
Z = [ones(T-1,1) diff(log(gnpn))];
y = diff(u);

Though this example removes missing values, the software can accommodate series containing missing values in the Kalman filter framework.

To determine how well the model forecasts observations, remove the last 10 observations for comparison.

numPeriods = 10;                   % Forecast horizon
isY = y(1:end-numPeriods);         % In-sample observations
oosY = y(end-numPeriods+1:end);    % Out-of-sample observations
ISZ = Z(1:end-numPeriods,:);       % In-sample predictors
OOSZ = Z(end-numPeriods+1:end,:);  % Out-of-sample predictors

Specify the coefficient matrices.

A = [NaN NaN; 0 0];
B = [1; 1];
C = [1 0];
D = NaN;

Specify the state-space model using ssm.

Mdl = ssm(A,B,C,D);

Estimate the model parameters, and use a random set of initial parameter values for optimization. Specify the regression component and its initial value for optimization using the 'Predictors' and 'Beta0' name-value pair arguments, respectively. Restrict the estimate of $σ$ to all positive, real numbers. For numerical stability, specify the Hessian when the software computes the parameter covariance matrix, using the 'CovMethod' name-value pair argument.

params0 = [0.3 0.2 0.1]; % Chosen arbitrarily
[EstMdl,estParams] = estimate(Mdl,isY,params0,'Predictors',ISZ,...
    'Beta0',[0.1 0.2],'lb',[-Inf,-Inf,0,-Inf,-Inf],'CovMethod','hessian');

Method: Maximum likelihood (fmincon)
Sample size: 51
Logarithmic  likelihood:     -87.2409
Akaike   info criterion:      184.482
Bayesian info criterion:      194.141
           |      Coeff       Std Err    t Stat     Prob  
----------------------------------------------------------
 c(1)      |  -0.31780       0.19429    -1.63572  0.10190 
 c(2)      |   1.21242       0.48882     2.48032  0.01313 
 c(3)      |   0.45583       0.63930     0.71302  0.47584 
 y <- z(1) |   1.32407       0.26313     5.03201   0      
 y <- z(2) | -24.48733       1.90115   -12.88024   0      
           |                                              
           |    Final State   Std Dev     t Stat    Prob  
 x(1)      |  -0.38117       0.42842    -0.88971  0.37363 
 x(2)      |   0.23402       0.66222     0.35339  0.72380

EstMdl is an ssm model, and you can access its properties using dot notation.

Forecast observations over the forecast horizon. EstMdl does not store the data set, so you must pass it in appropriate name-value pair arguments.

[fY,yMSE] = forecast(EstMdl,numPeriods,isY,'Predictors0',ISZ,...
    'PredictorsF',OOSZ,'Beta',estParams(end-1:end));

fY is a 10-by-1 vector containing the forecasted observations, and yMSE is a 10-by-1 vector containing the variances of the forecasted observations.

Obtain 95% Wald-type forecast intervals. Plot the forecasted observations with their true values and the forecast intervals.

ForecastIntervals(:,1) = fY - 1.96*sqrt(yMSE);
ForecastIntervals(:,2) = fY + 1.96*sqrt(yMSE);

figure
h = plot(dates(end-numPeriods-9:end-numPeriods),isY(end-9:end),'-k',...
    dates(end-numPeriods+1:end),oosY,'-k',...
    dates(end-numPeriods+1:end),fY,'--r',...
    dates(end-numPeriods+1:end),ForecastIntervals,':b',...
    dates(end-numPeriods:end-numPeriods+1),...
    [isY(end)*ones(3,1),[oosY(1);ForecastIntervals(1,:)']],':k',...
    'LineWidth',2);
xlabel('Period')
ylabel('Change in the unemployment rate')
legend(h([1,3,4]),{'Observations','Forecasted responses',...
    '95% forecast intervals'})
title('Observed and Forecasted Changes in the Unemployment Rate')

Figure contains an axes object. The axes object with title Observed and Forecasted Changes in the Unemployment Rate, xlabel Period, ylabel Change in the unemployment rate contains 8 objects of type line. These objects represent Observations, Forecasted responses, 95% forecast intervals.

This model seems to forecast the changes in the unemployment rate well.

Forecast States of State-Space Model

Open Live Script

Suppose that a latent process is an AR(1). The state equation is

$x_{t} = 0.5 x_{t - 1} + u_{t},$

where $u_{t}$ is Gaussian with mean 0 and standard deviation 1.

Generate a random series of 100 observations from $x_{t}$ , assuming that the series starts at 1.5.

T = 100;
ARMdl = arima('AR',0.5,'Constant',0,'Variance',1);
x0 = 1.5;
rng(1); % For reproducibility
x = simulate(ARMdl,T,'Y0',x0);

Suppose further that the latent process is subject to additive measurement error. The observation equation is

$y_{t} = x_{t} + ε_{t},$

where $ε_{t}$ is Gaussian with mean 0 and standard deviation 0.75. Together, the latent process and observation equations compose a state-space model.

Use the random latent state process (x) and the observation equation to generate observations.

y = x + 0.75*randn(T,1);

Specify the four coefficient matrices.

A = 0.5;
B = 1;
C = 1;
D = 0.75;

Specify the state-space model using the coefficient matrices.

Mdl = ssm(A,B,C,D);

Mdl is an ssm model.

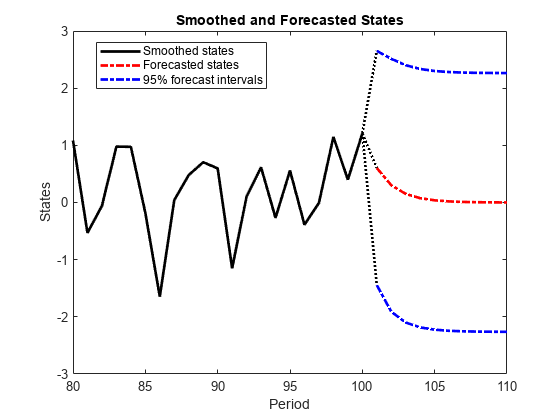
Forecast the states 10 periods into the future, and estimate their variances.

numPeriods = 10;
[~,~,ForecastedX,XMSE] = forecast(Mdl,numPeriods,y);

Plot the forecasts with the smoothed states, and 95% Wald-type forecast intervals.

smoothX = smooth(Mdl,y);
ForecastIntervals(:,1) = ForecastedX - 1.96*sqrt(XMSE);
ForecastIntervals(:,2) = ForecastedX + 1.96*sqrt(XMSE);

figure
plot(T-20:T,smoothX(T-20:T),'-k',T+1:T+numPeriods,ForecastedX,'-.r',...
    T+1:T+numPeriods,ForecastIntervals,'-.b',...
    T:T+1,[smoothX(end)*ones(3,1),[ForecastedX(1);ForecastIntervals(1,:)']],...
    ':k','LineWidth',2)
hold on
title({'Smoothed and Forecasted States'})
xlabel('Period')
ylabel('States')
legend({'Smoothed states','Forecasted states','95% forecast intervals'},...
    'Location','Best')
hold off

Figure contains an axes object. The axes object with title Smoothed and Forecasted States, xlabel Period, ylabel States contains 7 objects of type line. These objects represent Smoothed states, Forecasted states, 95% forecast intervals.

Input Arguments

collapse all

`Mdl` — Standard state-space model
`ssm` model object

Standard state-space model, specified as an ssm model object returned by ssm or estimate.

If Mdl is not fully specified (that is, Mdl contains unknown parameters), then specify values for the unknown parameters using the 'Params' name-value argument. Otherwise, the software issues an error. estimate returns fully-specified state-space models.

Mdl does not store observed responses or predictor data. Supply the data wherever necessary using the appropriate input or name-value arguments.

`numPeriods` — Forecast horizon
positive integer

Forecast horizon, specified as a positive integer. That is, the software returns 1,..,numPeriods forecasts.

Data Types: double

`Y0` — In-sample, observed responses
cell vector of numeric vectors | numeric matrix

In-sample, observed responses, specified as a cell vector of numeric vectors or a matrix.

If Mdl is time invariant, then Y0 is a T-by-n numeric matrix, where each row corresponds to a period and each column corresponds to a particular observation in the model. Therefore, T is the sample size and m is the number of observations per period. The last row of Y contains the latest observations.
If Mdl is time varying with respect to the observation equation, then Y is a T-by-1 cell vector. Each element of the cell vector corresponds to a period and contains an n_t-dimensional vector of observations for that period. The corresponding dimensions of the coefficient matrices in Mdl.C{t} and Mdl.D{t} must be consistent with the matrix in Y{t} for all periods. The last cell of Y contains the latest observations.

If Mdl is an estimated state-space model (that is, returned by estimate), then it is best practice to set Y0 to the same data set that you used to fit Mdl.

NaN elements indicate missing observations. For details on how the Kalman filter accommodates missing observations, see Algorithms.

Data Types: double | cell

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Beta',beta,'Predictors',Z specifies to deflate the observations by the regression component composed of the predictor data Z and the coefficient matrix beta.

`A` — Forecast-horizon, state-transition, coefficient matrices
cell vector of numeric matrices

Forecast-horizon, state-transition, coefficient matrices, specified as the comma-separated pair consisting of 'A' and a cell vector of numeric matrices.

A must contain at least numPeriods cells. Each cell must contain a matrix specifying how the states transition in the forecast horizon. If the length of A is greater than numPeriods, then the software uses the first numPeriods cells. The last cell indicates the latest period in the forecast horizon.
If Mdl is time invariant with respect to the states, then each cell of A must contain an m-by-m matrix, where m is the number of the in-sample states per period. By default, the software uses Mdl.A throughout the forecast horizon.
If Mdl is time varying with respect to the states, then the dimensions of the matrices in the cells of A can vary, but the dimensions of each matrix must be consistent with the matrices in B and C in the corresponding periods. By default, the software uses Mdl.A{end} throughout the forecast horizon.

Note

The matrices in A cannot contain NaN values.

Data Types: cell

`B` — Forecast-horizon, state-disturbance-loading, coefficient matrices
cell vector of matrices

Forecast-horizon, state-disturbance-loading, coefficient matrices, specified as the comma-separated pair consisting of 'B' and a cell vector of matrices.

B must contain at least numPeriods cells. Each cell must contain a matrix specifying how the states transition in the forecast horizon. If the length of B is greater than numPeriods, then the software uses the first numPeriods cells. The last cell indicates the latest period in the forecast horizon.
If Mdl is time invariant with respect to the states and state disturbances, then each cell of B must contain an m-by-k matrix, where m is the number of the in-sample states per period, and k is the number of in-sample, state disturbances per period. By default, the software uses Mdl.B throughout the forecast horizon.
If Mdl is time varying, then the dimensions of the matrices in the cells of B can vary, but the dimensions of each matrix must be consistent with the matrices in A in the corresponding periods. By default, the software uses Mdl.B{end} throughout the forecast horizon.

Note

The matrices in B cannot contain NaN values.

Data Types: cell

`C` — Forecast-horizon, measurement-sensitivity, coefficient matrices
cell vector of matrices

Forecast-horizon, measurement-sensitivity, coefficient matrices, specified as the comma-separated pair consisting of 'C' and a cell vector of matrices.

C must contain at least numPeriods cells. Each cell must contain a matrix specifying how the states transition in the forecast horizon. If the length of C is greater than numPeriods, then the software uses the first numPeriods cells. The last cell indicates the latest period in the forecast horizon.
If Mdl is time invariant with respect to the states and the observations, then each cell of C must contain an n-by-m matrix, where n is the number of the in-sample observations per period, and m is the number of in-sample states per period. By default, the software uses Mdl.C throughout the forecast horizon.
If Mdl is time varying with respect to the states or the observations, then the dimensions of the matrices in the cells of C can vary, but the dimensions of each matrix must be consistent with the matrices in A and D in the corresponding periods. By default, the software uses Mdl.C{end} throughout the forecast horizon.

Note

The matrices in C cannot contain NaN values.

Data Types: cell

`D` — Forecast-horizon, observation-innovation, coefficient matrices
cell vector of matrices

Forecast-horizon, observation-innovation, coefficient matrices, specified as the comma-separated pair consisting of 'D' and a cell vector of matrices.

D must contain at least numPeriods cells. Each cell must contain a matrix specifying how the states transition in the forecast horizon. If the length of D is greater than numPeriods, then the software uses the first numPeriods cells. The last cell indicates the latest period in the forecast horizon.
If Mdl is time invariant with respect to the observations and the observation innovations, then each cell of D must contain an n-by-h matrix, where n is the number of the in-sample observations per period, and h is the number of in-sample, observation innovations per period. By default, the software uses Mdl.D throughout the forecast horizon.
If Mdl is time varying with respect to the observations or the observation innovations, then the dimensions of the matrices in the cells of D can vary, but the dimensions of each matrix must be consistent with the matrices in C in the corresponding periods. By default, the software uses Mdl.D{end} throughout the forecast horizon.

Note

The matrices in D cannot contain NaN values.

Data Types: cell

`Beta` — Regression coefficients
`[]` (default) | numeric matrix

Regression coefficients corresponding to predictor variables, specified as the comma-separated pair consisting of 'Beta' and a d-by-n numeric matrix. d is the number of predictor variables (see Predictors0 and PredictorsF) and n is the number of observed response series (see Y0).

If you specify Beta, then you must also specify Predictors0 and PredictorsF.
If Mdl is an estimated state-space model, then specify the estimated regression coefficients stored in Mdl.estParams.

By default, the software excludes a regression component from the state-space model.

`Predictors0` — In-sample, predictor variables in state-space model observation equation
`[]` (default) | matrix

In-sample, predictor variables in the state-space model observation equation, specified as the comma-separated pair consisting of 'Predictors0' and a matrix. The columns of Predictors0 correspond to individual predictor variables. Predictors0 must have T rows, where row t corresponds to the observed predictors at period t (Z_t). The expanded observation equation is

$y_{t} - Z_{t} β = C x_{t} + D u_{t} .$

In other words, the software deflates the observations using the regression component. β is the time-invariant vector of regression coefficients that the software estimates with all other parameters.

If there are n observations per period, then the software regresses all predictor series onto each observation.
If you specify Predictors0, then Mdl must be time invariant. Otherwise, the software returns an error.
If you specify Predictors0, then you must also specify Beta and PredictorsF.
If Mdl is an estimated state-space model (that is, returned by estimate), then it is best practice to set Predictors0 to the same predictor data set that you used to fit Mdl.

By default, the software excludes a regression component from the state-space model.

Data Types: double

`PredictorsF` — Forecast-horizon, predictor variables in state-space model observation equation
`[]` (default) | numeric matrix

In-sample, predictor variables in the state-space model observation equation, specified as the comma-separated pair consisting of 'Predictors0' and a T-by-d numeric matrix. T is the number of in-sample periods and d is the number of predictor variables. Row t corresponds to the observed predictors at period t (Z_t). The expanded observation equation is

$y_{t} - Z_{t} β = C x_{t} + D u_{t} .$

If there are n observations per period, then the software regresses all predictor series onto each observation.
If you specify Predictors0, then Mdl must be time invariant. Otherwise, the software returns an error.
If you specify Predictors0, then you must also specify Beta and PredictorsF.
If Mdl is an estimated state-space model (that is, returned by estimate), then it is best practice to set Predictors0 to the same predictor data set that you used to fit Mdl.

By default, the software excludes a regression component from the state-space model.

Data Types: double

Output Arguments

collapse all

`Y` — Forecasted observations
matrix | cell vector of numeric vectors

Forecasted observations, returned as a matrix or a cell vector of numeric vectors.

If Mdl is a time-invariant, state-space model with respect to the observations, then Y is a numPeriods-by-n matrix.

If Mdl is a time-varying, state-space model with respect to the observations, then Y is a numPeriods-by-1 cell vector of numeric vectors. Cell t of Y contains an n_t-by-1 numeric vector of forecasted observations for period t.

`YMSE` — Error variances of forecasted observations
matrix | cell vector of numeric vectors

Error variances of forecasted observations, returned as a matrix or a cell vector of numeric vectors.

If Mdl is a time-invariant, state-space model with respect to the observations, then YMSE is a numPeriods-by-n matrix.

If Mdl is a time-varying, state-space model with respect to the observations, then YMSE is a numPeriods-by-1 cell vector of numeric vectors. Cell t of YMSE contains an n_t-by-1 numeric vector of error variances for the corresponding forecasted observations for period t.

`X` — State forecasts
matrix | cell vector of numeric vectors

State forecasts, returned as a matrix or a cell vector of numeric vectors.

If Mdl is a time-invariant, state-space model with respect to the states, then X is a numPeriods-by-m matrix.

If Mdl is a time-varying, state-space model with respect to the states, then X is a numPeriods-by-1 cell vector of numeric vectors. Cell t of X contains an m_t-by-1 numeric vector of forecasted observations for period t.

`XMSE` — Error variances of state forecasts
matrix | cell vector of numeric vectors

Error variances of state forecasts, returned as a matrix or a cell vector of numeric vectors.

If Mdl is a time-invariant, state-space model with respect to the states, then XMSE is a numPeriods-by-m matrix.

If Mdl is a time-varying, state-space model with respect to the states, then XMSE is a numPeriods-by-1 cell vector of numeric vectors. Cell t of XMSE contains an m_t-by-1 numeric vector of error variances for the corresponding forecasted observations for period t.

Tips

Mdl does not store the response data, predictor data, and the regression coefficients. Supply them whenever necessary using the appropriate input or name-value pair arguments.

Algorithms

The Kalman filter accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose there is a missing observation at period t. Then, the state forecast for period t based on the previous t – 1 observations and filtered state for period t are equivalent.
For explicitly defined state-space models, forecast applies all predictors to each response series. However, each response series has its own set of regression coefficients.

References

[1] Durbin J., and S. J. Koopman. Time Series Analysis by State Space Methods. 2nd ed. Oxford: Oxford University Press, 2012.

Version History

Introduced in R2014a

forecast

Syntax

Description

Examples

Forecast Observations of Time-Invariant State-Space Model

Forecast Observations of State-Space Model Containing Regression Component

Forecast States of State-Space Model

Input Arguments

`Mdl` — Standard state-space model
`ssm` model object

`numPeriods` — Forecast horizon
positive integer

`Y0` — In-sample, observed responses
cell vector of numeric vectors | numeric matrix

Name-Value Arguments

`A` — Forecast-horizon, state-transition, coefficient matrices
cell vector of numeric matrices

`B` — Forecast-horizon, state-disturbance-loading, coefficient matrices
cell vector of matrices

`C` — Forecast-horizon, measurement-sensitivity, coefficient matrices
cell vector of matrices

`D` — Forecast-horizon, observation-innovation, coefficient matrices
cell vector of matrices

`Beta` — Regression coefficients
`[]` (default) | numeric matrix

`Predictors0` — In-sample, predictor variables in state-space model observation equation
`[]` (default) | matrix

`PredictorsF` — Forecast-horizon, predictor variables in state-space model observation equation
`[]` (default) | numeric matrix

Output Arguments

`Y` — Forecasted observations
matrix | cell vector of numeric vectors

`YMSE` — Error variances of forecasted observations
matrix | cell vector of numeric vectors

`X` — State forecasts
matrix | cell vector of numeric vectors

`XMSE` — Error variances of state forecasts
matrix | cell vector of numeric vectors

Tips

Algorithms

References

Version History

See Also

Topics

forecast

Syntax

Description

Examples

Forecast Observations of Time-Invariant State-Space Model

Forecast Observations of State-Space Model Containing Regression Component

Forecast States of State-Space Model

Input Arguments

Mdl — Standard state-space model ssm model object

numPeriods — Forecast horizon positive integer

Y0 — In-sample, observed responses cell vector of numeric vectors | numeric matrix

Name-Value Arguments

A — Forecast-horizon, state-transition, coefficient matrices cell vector of numeric matrices

B — Forecast-horizon, state-disturbance-loading, coefficient matrices cell vector of matrices

C — Forecast-horizon, measurement-sensitivity, coefficient matrices cell vector of matrices

D — Forecast-horizon, observation-innovation, coefficient matrices cell vector of matrices

Beta — Regression coefficients [] (default) | numeric matrix

Predictors0 — In-sample, predictor variables in state-space model observation equation [] (default) | matrix

PredictorsF — Forecast-horizon, predictor variables in state-space model observation equation [] (default) | numeric matrix

Output Arguments

Y — Forecasted observations matrix | cell vector of numeric vectors

YMSE — Error variances of forecasted observations matrix | cell vector of numeric vectors

X — State forecasts matrix | cell vector of numeric vectors

XMSE — Error variances of state forecasts matrix | cell vector of numeric vectors

Tips

Algorithms

References

Version History

See Also

Topics

`Mdl` — Standard state-space model
`ssm` model object

`numPeriods` — Forecast horizon
positive integer

`Y0` — In-sample, observed responses
cell vector of numeric vectors | numeric matrix

`A` — Forecast-horizon, state-transition, coefficient matrices
cell vector of numeric matrices

`B` — Forecast-horizon, state-disturbance-loading, coefficient matrices
cell vector of matrices

`C` — Forecast-horizon, measurement-sensitivity, coefficient matrices
cell vector of matrices

`D` — Forecast-horizon, observation-innovation, coefficient matrices
cell vector of matrices

`Beta` — Regression coefficients
`[]` (default) | numeric matrix

`Predictors0` — In-sample, predictor variables in state-space model observation equation
`[]` (default) | matrix

`PredictorsF` — Forecast-horizon, predictor variables in state-space model observation equation
`[]` (default) | numeric matrix

`Y` — Forecasted observations
matrix | cell vector of numeric vectors

`YMSE` — Error variances of forecasted observations
matrix | cell vector of numeric vectors

`X` — State forecasts
matrix | cell vector of numeric vectors

`XMSE` — Error variances of state forecasts
matrix | cell vector of numeric vectors