simulate

Simulate sample paths of threshold-switching dynamic regression model

Since R2021b

Syntax

Y = simulate(Mdl,numObs)

Y = simulate(Mdl,numObs,Name,Value)

[Y,E,StatePaths] = simulate(___)

Description

Y = simulate(Mdl,numObs) returns a random numObs-period path of response series Y from simulating the fully specified threshold-switching dynamic regression model Mdl.

example

Y = simulate(Mdl,numObs,Name,Value) uses additional options specified by one or more name-value arguments. For example, simulate(Mdl,10,NumPaths=1000,Y0=Y0) simulates 1000 sample paths of length 10, and initializes the dynamic component of each submodel by using the presample response data Y0.

example

[Y,E,StatePaths] = simulate(___) also returns the simulated innovation paths E and the simulated state paths StatePaths, using any of the input argument combinations in the previous syntaxes.

example

Examples

collapse all

Simulate Response Path from SETAR Model

Open Live Script

Suppose a data-generating process (DGP) is a two-state, self-exciting threshold autoregressive (SETAR) model for a 1-D response variable. Specify all parameter values (this example uses arbitrary values).

Create Fully Specified Model for DGP

Create a discrete threshold transition at level 0. Label the regimes to reflect the state of the economy:

When the threshold variable (currently unknown) is in $(- \infty, 0)$ , the economy is in a recession.

When the threshold variable is in $[0, \infty)$ , the economy is expanding.

t = 0;
tt = threshold(t,StateNames=["Recession" "Expansion"])

tt = 
  threshold with properties:

          Type: 'discrete'
        Levels: 0
         Rates: []
    StateNames: ["Recession"    "Expansion"]
     NumStates: 2

tt is a fully specified threshold object that describes the switching mechanism of the threshold-switching model.

Assume the following univariate models describe the response process of the system:

Recession: $y_{t} = - 1 + 0.1 y_{t - 1} + ε_{1, t}$ , where $ε_{1, t} \sim Ν (0, 1)$ .
Expansion: $y_{t} = 1 + + 0.3 y_{t - 1} + 0.2 y_{t - 2} + ε_{2, t}$ , where $ε_{2, t} \sim Ν (0, 2^{2})$ .

For each regime, use arima to create an AR model that describes the response process within the regime.

c1 = -1;
c2 = 1;
ar1 = 0.1;       
ar2 = [0.3 0.2]; 
v1 = 1;
v2 = 4;

mdl1 = arima(Constant=c1,AR=ar1,Variance=v1,...
    Description="Recession State Model")

mdl1 = 
  arima with properties:

     Description: "Recession State Model"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 1
               D: 0
               Q: 0
        Constant: -1
              AR: {0.1} at lag [1]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 1
 
   ARIMA(1,0,0) Model (Gaussian Distribution)

mdl2 = arima(Constant=c2,AR=ar2,Variance=v2,...
    Description="Expansion State Model")

mdl2 = 
  arima with properties:

     Description: "Expansion State Model"
      SeriesName: "Y"
    Distribution: Name = "Gaussian"
               P: 2
               D: 0
               Q: 0
        Constant: 1
              AR: {0.3 0.2} at lags [1 2]
             SAR: {}
              MA: {}
             SMA: {}
     Seasonality: 0
            Beta: [1×0]
        Variance: 4
 
   ARIMA(2,0,0) Model (Gaussian Distribution)

mdl1 and mdl2 are fully specified arima objects.

Store the submodels in a vector with order corresponding to the regimes in tt.StateNames.

mdl = [mdl1; mdl2];

Use tsVAR to create a TAR model from the switching mechanism tt and the state-specific submodels mdl.

Mdl = tsVAR(tt,mdl)

Mdl = 
  tsVAR with properties:

         Switch: [1x1 threshold]
      Submodels: [2x1 varm]
      NumStates: 2
      NumSeries: 1
     StateNames: ["Recession"    "Expansion"]
    SeriesNames: "1"
     Covariance: []

Mdl.Submodels(2)

ans = 
  varm with properties:

     Description: "AR-Stationary 1-Dimensional VAR(2) Model"
     SeriesNames: "Y1" 
       NumSeries: 1
               P: 2
        Constant: 1
              AR: {0.3 0.2} at lags [1 2]
           Trend: 0
            Beta: [1×0 matrix]
      Covariance: 4

Mdl is a fully specified tsVAR object representing a univariate two-state TAR model. tsVAR stores specified arima submodels as varm objects.

Simulate Response Data from DGP

Generate one random response path of length 50 from the model. simulate assumes that the threshold variable is $y_{t - 1}$ , which implies that the model is self-exciting.

rng(1); % For reproducibility
y = simulate(Mdl,50);

y is a 50-by-1 vector of one response path.

Plot the response path with the threshold by using ttplot.

figure
ttplot(Mdl.Switch,Data=y)

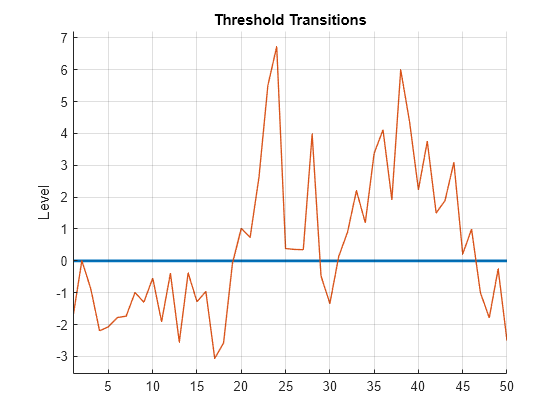
Figure contains an axes object. The axes object with title Threshold Transitions, ylabel Level contains 2 objects of type line.

Simulate Multiple Paths

Open Live Script

Consider the following logistic TAR (LSTAR) model for the annual, CPI-based, Canadian inflation rate series $y_{t}$ .

State 1: $y_{t} = - 5 + ε_{1, t}$ , where $ε_{1, t} \sim Ν (0, 0 . 1^{2}) .$
State 2: $y_{t} = ε_{2, t}$ , where $ε_{2, t} \sim Ν (0, 0 . 2^{2}) .$
State 3: $y_{t} = 5 + ε_{3, t}$ , where $ε_{3, t} \sim Ν (0, 0 . 3^{2}) .$
The system is in state 1 when $y_{t} < 2$ , the system is in state 2 when $2 \leq y_{t} < 8$ , and the system is in state 3 otherwise.
The transition function rate between states 1 and 2 is 3.5, and the transition function rate between states 2 and 3 is 1.5.

Create an LSTAR model representing $y_{t}$ .

t = [2 8];
tt = threshold([2 8],Type="logistic",Rates=[3.5 1.5]);
  
mdl1 = arima(Constant=-5,Variance=0.1);
mdl2 = arima(Constant=0,Variance=0.2);
mdl3 = arima(Constant=5,Variance=0.3);
  
Mdl = tsVAR(tt,[mdl1; mdl2; mdl3]);

Load the Canadian inflation and interest rate data set.

load Data_Canada

Extract the CPI-based inflation rate series.

INF_C = DataTable.INF_C; 
numObs = length(INF_C);

Simulate ten paths from the model. Specify the threshold variable type and its data.

Y = simulate(Mdl,numObs,NumPaths=10,Type="exogenous",Z=INF_C);

Y is a numObs-by-10 matrix of simulated paths. Each column represents an independently simulated path.

In a tiled layout, plot the threshold transitions with the data by using ttplot,and plot the simulated paths to one tile.

tiledlayout(2,1)
nexttile
ttplot(tt,Data=INF_C)
colorbar('off')
xticklabels(dates(xticks))
nexttile
plot(dates,Y)
grid on
axis tight
title("Simulations")

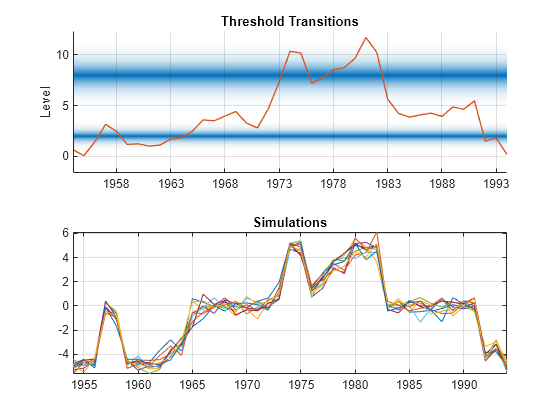
Figure contains 2 axes objects. Axes object 1 with title Threshold Transitions, ylabel Level contains 3 objects of type patch, line. Axes object 2 with title Simulations contains 10 objects of type line.

Y switches between submodels according to the value of the threshold variable INF_C. Mixing is evident for observations near thresholds, such as at the inflation rates of 1964 and 1978.

Return Innovations and States

Open Live Script

Consider the model for the annual, CPI-based, Canadian inflation rate series in Simulate Multiple Paths.

Create the LSTAR model for the series.

t = [2 8];
tt = threshold([2 8],Type="logistic",Rates=[3.5 1.5]);
  
mdl1 = arima(Constant=-5,Variance=0.1);
mdl2 = arima(Constant=0,Variance=0.2);
mdl3 = arima(Constant=5,Variance=0.3);
  
Mdl = tsVAR(tt,[mdl1; mdl2; mdl3]);

Load the Canadian inflation and interest rate data set and extract the inflation rate series.

load Data_Canada
INF_C = DataTable.INF_C; 
numObs = length(INF_C);

Simulate a length numObs path from the model. Specify the threshold variable type and its data. Return the innovations and states.

[y,e,s] = simulate(Mdl,numObs,NumPaths=10,Type="exogenous",Z=INF_C);

tiledlayout(3,1)
nexttile
plot(y);
ylabel("Simulated Response")
grid on

nexttile
plot(e)
ylabel('Innovation')
grid on

nexttile
stem(s)
ylabel('State')
yticks([1 2 3])
yticklabels(Mdl.StateNames)

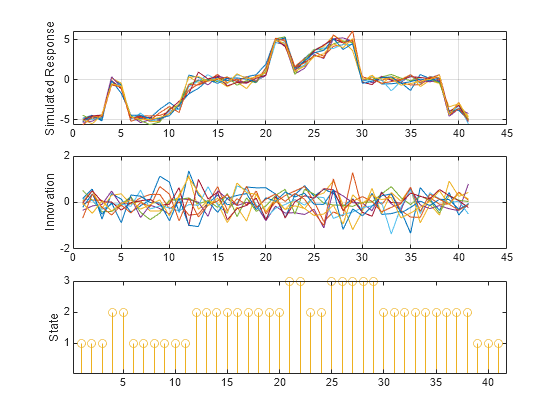
Figure contains 3 axes objects. Axes object 1 with ylabel Simulated Response contains 10 objects of type line. Axes object 2 with ylabel Innovation contains 10 objects of type line. Axes object 3 with ylabel State contains 10 objects of type stem.

Initialize Multivariate Model Simulation from Multiple Starting Conditions

Open Live Script

This example shows how to initialize simulated paths from presample responses and initial states. The example uses arbitrary parameter values.

Fully Specify LSETAR Model

Consider the following 2-D LSETAR model.

State 1, "Low": $y_{t} = [\begin{array}{cccccccccccccccccccc} 1 \\ - 1 \end{array}] + ε_{1, t},$ where $ε_{1, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 1 & - 0.1 \\ - 0.1 & 1 \end{array}]) .$
State 2 , "Med": $y_{t} = [\begin{array}{cccccccccccccccccccc} 2 \\ - 2 \end{array}] + [\begin{array}{cccccccccccccccccccc} 0.5 & 0.1 \\ 0.5 & 0.5 \end{array}] y_{t - 1} + ε_{2, t},$ where $ε_{2, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 2 & - 0.2 \\ - 0.2 & 2 \end{array}]) .$
State 3, "High": $y_{t} = [\begin{array}{cccccccccccccccccccc} 3 \\ - 3 \end{array}] + [\begin{array}{cccccccccccccccccccc} 0.25 & 0 \\ 0 & 0 \end{array}] y_{t - 1} + [\begin{array}{cccccccccccccccccccc} 0 & 0 \\ 0.25 & 0 \end{array}] y_{t - 2} + ε_{3, t},$ where $ε_{3, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 3 & - 0.3 \\ - 0.3 & 3 \end{array}]) .$
The system is in state 1 when $y_{2, t - 4} < - 1$ , the system is in state 2 when $- 1 \leq y_{2, t - 4} < 1$ , and the system is in state 3 otherwise.
The transition function is logistic. The transition rate from state 1 to 2 is 3.5, and the transition rate from state 1 to 3 is 1.5.

Create logistic threshold transitions at mid-levels -1 and 1 with rates 3.5 and 1.5, respectively. Label the states.

t = [-1 1];
r = [3.5 1.5];
stateNames = ["Low" "Med" "High"];
tt = threshold(t,Type="logistic",Rates=[3.5 1.5],StateNames=stateNames);

Create the VAR submodels by using varm. Store the submodels in a vector with order corresponding to the regimes in tt.StateNames.

% Constants (numSeries x 1 vectors)
C1 = [1; -1];
C2 = [2; -2];
C3 = [3; -3];

% Autoregression coefficients (numSeries x numSeries matrices)
AR1 = {};                            % 0 lags
AR2 = {[0.5 0.1; 0.5 0.5]};          % 1 lag
AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; % 2 lags

% Innovations covariances (numSeries x numSeries matrices)
Sigma1 = [1 -0.1; -0.1 1];
Sigma2 = [2 -0.2; -0.2 2];
Sigma3 = [3 -0.3; -0.3 3];

% VAR Submodels
mdl1 = varm('Constant',C1,'AR',AR1,'Covariance',Sigma1);
mdl2 = varm('Constant',C2,'AR',AR2,'Covariance',Sigma2);
mdl3 = varm('Constant',C3,'AR',AR3,'Covariance',Sigma3);

mdl = [mdl1; mdl2; mdl3];

Create an LSETAR model from the switching mechanism tt and the state-specific submodels mdl. Label the series Y1 and Y2.

Mdl = tsVAR(tt,mdl,SeriesNames=["Y1" "Y2"])

Mdl = 
  tsVAR with properties:

         Switch: [1x1 threshold]
      Submodels: [3x1 varm]
      NumStates: 3
      NumSeries: 2
     StateNames: ["Low"    "Med"    "High"]
    SeriesNames: ["Y1"    "Y2"]
     Covariance: []

Mdl is a fully specified tsVAR object representing a multivariate three-state LSETAR model. tsVAR object functions enable you to specify threshold variable characteristics and data.

Initialize Simulation from Presample Responses

Consider simulating 5 paths initialized from presample responses. Specify a numPreObs-by-numSeries-by-numPaths array of presample responses, where:

numPreObs is the number of presample responses per series and path. You must specify enough presample observations to initialize all AR components in the VAR models and the endogenous threshold variable. The largest AR component order is 2 and the threshold variable delay is 4, therefore simulate requires numPreObs=4 presample observations per series and path.
numSeries=2, the number of response series in the system.
numPaths=5, the number of independent paths to simulate.

delay = 4;
numPaths = 5;
Y0 = zeros(delay,Mdl.NumSeries,numPaths);
for j = 2:numPaths
    Y0(:,:,j) = 10*j*ones(delay,Mdl.NumSeries);
end

Simulate 10 paths of length 100 from the LSETAR model from the presample. Specify the endogenous threshold variable and its delay, $y_{2, t - 4}$ .

numObs = 100;
rng(1);
Y = simulate(Mdl,numObs,NumPaths=numPaths,Y0=Y0,Index=2,Delay=4);

Y is a 100-by-2-by-5 array of simulate response paths. For example, Y(50,2,3) is the simulated response of path 3, of series Y2, at time point 50.

Plot the simulated paths for each variable on separate plots.

tiledlayout(2,1)
nexttile
plot(squeeze(Y(:,1,:)))
title("Y1")
nexttile
plot(squeeze(Y(:,2,:)))
title("Y2")

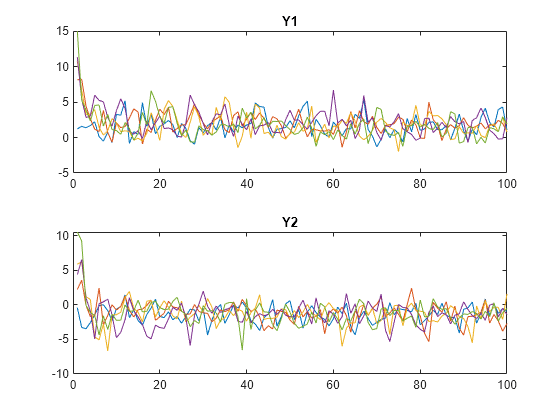
Figure contains 2 axes objects. Axes object 1 with title Y1 contains 5 objects of type line. Axes object 2 with title Y2 contains 5 objects of type line.

The system quickly settles regardless of the presample.

Initialize Simulation from States

Simulate three paths of length 100, where each of the three states initialize a path. Specify state indices for initialization, and specify the endogenous threshold variable and its delay.

S0 = 1:Mdl.NumStates;
numPaths = numel(S0);
Y = simulate(Mdl,numObs,NumPaths=numPaths,S0=S0,Index=2,Delay=4);
tiledlayout(2,1)
nexttile
plot(squeeze(Y(:,1,:)))
title("Y1")
nexttile
plot(squeeze(Y(:,2,:)))
title("Y2")

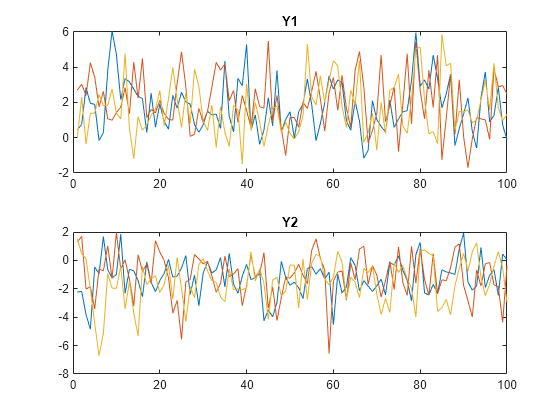
Figure contains 2 axes objects. Axes object 1 with title Y1 contains 3 objects of type line. Axes object 2 with title Y2 contains 3 objects of type line.

Simulate Model Containing Exogenous Regression Component

Open Live Script

Consider including regression components for exogenous variables in each submodel of the threshold-switching dynamic regression model in Initialize Multivariate Model Simulation from Multiple Starting Conditions.

Fully Specify LSETAR Model

Create logistic threshold transitions at mid-levels -1 and 1 with rates 3.5 and 1.5, respectively. Label the states.

t = [-1 1];
r = [3.5 1.5];
stateNames = ["Low" "Med" "High"];
tt = threshold(t,Type="logistic",Rates=[3.5 1.5],StateNames=stateNames)

tt = 
  threshold with properties:

          Type: 'logistic'
        Levels: [-1 1]
         Rates: [3.5000 1.5000]
    StateNames: ["Low"    "Med"    "High"]
     NumStates: 3

Assume the following VARX models describe the response processes of the system:

State 1: $y_{t} = [\begin{array}{cccccccccccccccccccc} 1 \\ - 1 \end{array}] + [\begin{array}{cccccccccccccccccccc} 1 \\ - 1 \end{array}] x_{1, t} + ε_{1, t},$ where $ε_{1, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 1 & - 0.1 \\ - 0.1 & 1 \end{array}]) .$
State 2: $y_{t} = [\begin{array}{cccccccccccccccccccc} 2 \\ - 2 \end{array}] + [\begin{array}{cccccccccccccccccccc} 2 & 2 \\ - 2 & - 2 \end{array}] x_{2, t} + [\begin{array}{cccccccccccccccccccc} 0.5 & 0.1 \\ 0.5 & 0.5 \end{array}] y_{t - 1} + ε_{2, t},$ where $ε_{2, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 2 & - 0.2 \\ - 0.2 & 2 \end{array}]) .$
State 3: $y_{t} = [\begin{array}{cccccccccccccccccccc} 3 \\ - 3 \end{array}] + [\begin{array}{cccccccccccccccccccc} 3 & 3 & 3 \\ - 3 & - 3 & - 3 \end{array}] x_{3, t} + [\begin{array}{cccccccccccccccccccc} 0.25 & 0 \\ 0 & 0 \end{array}] y_{t - 1} + [\begin{array}{cccccccccccccccccccc} 0 & 0 \\ 0.25 & 0 \end{array}] y_{t - 2} + ε_{3, t},$ where $ε_{3, t} \sim N ([\begin{array}{cccccccccccccccccccc} 0 \\ 0 \end{array}], [\begin{array}{cccccccccccccccccccc} 3 & - 0.3 \\ - 0.3 & 3 \end{array}]) .$

$x_{1, t}$ represents a single exogenous variable, $x_{2, t}$ represents two exogenous variables, and $x_{3, t}$ represents three exogenous variables. Store the submodels in a vector.

% Constants (numSeries x 1 vectors)
C1 = [1; -1];
C2 = [2; -2];
C3 = [3; -3];

% Regression coefficients (numSeries x numRegressors matrices)
Beta1 = [1; -1];            % 1 regressor
Beta2 = [2 2; -2 -2];       % 2 regressors
Beta3 = [3 3 3; -3 -3 -3];  % 3 regressors

% Autoregression coefficients (numSeries x numSeries matrices)
AR1 = {};                            
AR2 = {[0.5 0.1; 0.5 0.5]};          
AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; 

% Innovations covariances (numSeries x numSeries matrices)
Sigma1 = [1 -0.1; -0.1 1];
Sigma2 = [2 -0.2; -0.2 2];
Sigma3 = [3 -0.3; -0.3 3];

%VARX submodels
mdl1 = varm(Constant=C1,AR=AR1,Beta=Beta1,Covariance=Sigma1);
mdl2 = varm(Constant=C2,AR=AR2,Beta=Beta2,Covariance=Sigma2);
mdl3 = varm(Constant=C3,AR=AR3,Beta=Beta3,Covariance=Sigma3);

mdl = [mdl1; mdl2; mdl3];

Create an LSETAR model from the switching mechanism tt and the state-specific submodels mdl. Label the series Y1 and Y2.

Mdl = tsVAR(tt,mdl,SeriesNames=["Y1" "Y2"])

Mdl = 
  tsVAR with properties:

         Switch: [1x1 threshold]
      Submodels: [3x1 varm]
      NumStates: 3
      NumSeries: 2
     StateNames: ["Low"    "Med"    "High"]
    SeriesNames: ["Y1"    "Y2"]
     Covariance: []

Simulate Data Ignoring Regression Component

If you do not supply exogenous data, simulate ignores the regression components in the submodels. Simulate a single path of responses, innovations, and states into a simulation horizon of length 50. Then plot each path separately.

rng(1); % For reproducibility
numObs = 50;
[Y,E,SP] = simulate(Mdl,numObs);

figure
tiledlayout(3,1)
nexttile
plot(Y)
ylabel("Response")
grid on
legend(["y_1" "y_2"])
nexttile
plot(E)
ylabel("Innovation")
grid on
legend(["e_1" "e_2"])
nexttile
stem(SP)
ylabel("State")
yticks([1 2 3])

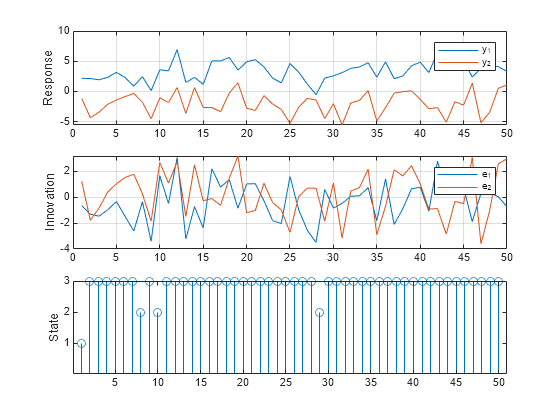
Figure contains 3 axes objects. Axes object 1 with ylabel Response contains 2 objects of type line. These objects represent y_1, y_2. Axes object 2 with ylabel Innovation contains 2 objects of type line. These objects represent e_1, e_2. Axes object 3 with ylabel State contains an object of type stem.

Simulate Data Including Regression Component

simulate requires exogenous data in order to generate random paths from the model. Simulate exogenous data for the three regressors by generating 50 random observations from the 3-D standard Gaussian distribution.

X = randn(50,3);

Generate one random response, innovation, and state path of length 50. Specify the simulated exogenous data for the submodel regression components. Plot the results.

rng(1); % Reset seed for comparison
[Y,E,SP] = simulate(Mdl,numObs,X=X);

figure
tiledlayout(3,1)
nexttile
plot(Y)
ylabel("Response")
grid on
legend(["y_1" "y_2"])
nexttile
plot(E)
ylabel("Innovation")
grid on
legend(["e_1" "e_2"])
nexttile
stem(SP)
ylabel("State")
yticks([1 2 3])

Perform Monte Carlo Estimation

Open Live Script

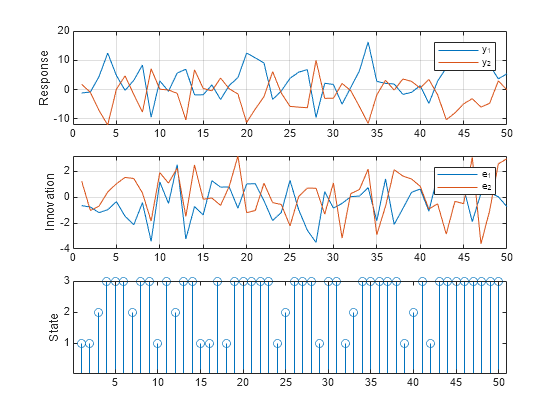
This example shows how to use Monte Carlo estimation to obtain an interval estimate of the threshold mid-level.

Consider a SETAR model for the real US GDP growth rate $y_{t}$ with AR(4) submodels. Suppose the threshold variable is $y_{t}$ (self exciting with 0 delay).

Create a discrete threshold transition at unknown mid-level $t_{1}$ . Label the states "Recession" and "Expansion".

tt = threshold(NaN,StateNames=["Recession" "Expansion"]);

For each state, create a partially specified AR(4) model with one coefficient at lag 4. Store the state submodels in a vector.

submdl = arima(ARLags=4);
mdl = [submdl; submdl];

Each submodel has an unknown, estimable lag 4 coefficient, model constant, and innovations variance.

Create a partially specified TAR model from the threshold transition and submodel vector.

Mdl = tsVAR(tt,mdl);

Create a fully specified threshold transition that has the same structure as tt, but set the mid-level to 0.

tt0 = threshold(0);

Load the US macroeconomic data set. Compute the real GDP growth rate as a percent.

load Data_USEconModel
rGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF;
pRGDP = 100*price2ret(rGDP);
T = numel(pRGDP);

Fit the TAR to the real GDP rate series.

EstMdl = estimate(Mdl,tt0,pRGDP,Z=pRGDP,Type="exogenous");

Simulate 100 response paths from the estimated model.

rng(100) % For reproducibility
numPaths= 100;
Y = simulate(EstMdl,T,NumPaths=numPaths,Z=pRGDP,Type="exogenous");

Fit the TAR model to each simulated response path. Specify the estimated threshold transition EstMdl.Switch to initialize the estimation procedure. For each path, store the estimated threshold transition mid-level.

tMC = nan(T,1);
for j = 1:numPaths
    EstMdlSim = estimate(Mdl,EstMdl.Switch,Y(:,j),Z=Y(:,j),Type="exogenous");
    tMC(j) = EstMdlSim.Switch.Levels;
end

tMC is a 100-by-1 vector representing a Monte Carlo sample of threshold transitions.

Obtain a 95% confidence interval on the true threshold transition by computing the 0.25 and .975 quantiles of the Monte Carlo sample.

tCI = quantile(tMC,[0.025 0.975])

tCI = 1×2

    0.5158    0.9810

A 95% confidence interval on the true threshold transition is (0.52%, 0.98%).

Input Arguments

collapse all

`Mdl` — Fully specified threshold-switching dynamic regression model
`tsVAR` model object

Fully specified threshold-switching dynamic regression model, specified as an tsVAR model object returned by tsVAR or estimate. Properties of a fully specified model object do not contain NaN values.

`numObs` — Number of observations to generate
positive integer

Number of observations to generate for each sample path, specified as a positive integer.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: NumPaths=1000,Y0=Y0 simulates 1000 sample paths and initializes the dynamic component of each submodel by using the presample response data Y0.

`NumPaths` — Number of sample paths to generate
`1` (default) | positive integer

Number of sample paths to generate, specified as a positive integer.

Example: NumPaths=1000

Data Types: double

`Type` — Type of threshold variable data
`"endogenous"` (default) | `"exogenous"`

Type of threshold variable data, specified as a value in this table.

Value Description

Value	Description
`"endogenous"`	The model is self-exciting with threshold variable data $z_{t} = y_{j, (t - d)},$ generated by response j, where The name-value argument `'Delay'` specifies the delay d. The name-value argument `'Index'` specifies the component j of the multivariate response variable.
`"exogenous"`	The threshold variable is exogenous to the system. The name-value argument `'Z'` specifies the threshold variable data and is required.

"endogenous"

The model is self-exciting with threshold variable data $z_{t} = y_{j, (t - d)},$ generated by response j, where

The name-value argument 'Delay' specifies the delay d.
The name-value argument 'Index' specifies the component j of the multivariate response variable.

"exogenous" The threshold variable is exogenous to the system. The name-value argument 'Z' specifies the threshold variable data and is required.

Example: Type="exogenous",Z=z specifies the data z for the exogenous threshold variable.

Example: Type="endogenous",Index=2,Delay=4 specifies the endogenous threshold variable as y_2,t−4, whose data is Y(:,2).

Data Types: char | string | cell

`Y0` — Presample response data
numeric matrix | numeric array

Presample response data, specified as a numeric matrix or array.

To use the same presample data for each of the numPaths path, specify a numPreSampleObs-by-numSeries matrix, where numPaths is the value of NumPaths, numPreSampleObs is the number of presample observations, and numSeries is the number of response variables.

To use different presample data for each path:

For univariate ARX submodels, specify a numPreSampleObs-by-numPaths matrix.
For multivariate VARX submodels, specify a numPreSampleObs-by-numSeries-by-numPaths array.

The number of presample observations numPreSampleObs must be sufficient to initialize the AR terms of all submodels. For models of type "endogenous", the number of presample observations must also be sufficient to initialize the delayed response. If numPreSampleObs exceeds the number necessary to initial the model, simulate uses only the latest observations. The last row contains the latest observations.

simulate updates Y0 using the latest simulated observations each time it switches states.

By default, simulate determines Y0 by the submodel of the initial state:

If the initial submodel is a stationary AR process without regression components, simulate sets presample observations to the unconditional mean.
Otherwise, simulate sets presample observations to zero.

Data Types: double

`Z` — Threshold variable data z_t
empty array (`[]`) (default) | numeric vector | numeric matrix

Threshold variable data for simulations of type "exogenous", specified as a numeric vector of length numObsZ or a numObsZ-by-numPaths numeric matrix.

For a numeric vector, simulate applies the same data to all simulated paths. For a matrix, simulate applies columns of Z to corresponding simulated paths.

If numObsZ exceeds numobs, simulate uses only the latest observations. The last row contains the latest observation.

simulate determines the initial state of simulations by values in the first row Z(1,:).

Data Types: double

`Delay` — Threshold variable delay d in y_j,t−d
`1` (default) | positive integer

Threshold variable delay d in y_j,t−d for simulations of type "endogenous", specified as a positive integer.

Example: Delay=4 specifies that the threshold variable is y_2,t−d, where j is the value of Index.

Data Types: double

`Index` — Threshold variable index j in y_j,t−d
`1` (default) | scalar in `1:Mdl.NumSeries`

Threshold variable index j in y_j,t−d for simulations of type "endogenous", specified as a scalar in 1:Mdl.NumSeries.

simulate ignores Index for univariate AR models.

Example: Index=2 specifies that the threshold variable is y_2,t−d, where d is the value of Delay.

Data Types: double

`S0` — Initial states
`1` (default) | numeric scalar | numeric vector

Initial states of simulations, for simulations of type "endogenous", specified as a numeric scalar or vector of length numPaths. Entries of S0 must be in 1:Mdl.NumStates.

A scalar S0 applies the same initial state to all paths. A vector S0 applies initial state S0(j) to path j.

If you specify Y0, simulate ignores S0 and determines initial states by the specified presample data.

Example: 'S0',2 applies state 2 to initialize all paths.

Example: 'S0',[2 3] specifies state 2 as the initial state.

Data Types: double

`X` — Predictor data
numeric matrix | cell vector of numeric matrices

Predictor data used to evaluate regression components in all submodels of Mdl, specified as a numeric matrix or a cell vector of numeric matrices.

To use a subset of the same predictors in each state, specify X as a matrix with numPreds columns and at least numObs rows. Columns correspond to distinct predictor variables. Submodels use initial columns of the associated matrix, in order, up to the number of submodel predictors. The number of columns in the Beta property of Mdl.SubModels(j) determines the number of exogenous variables in the regression component of submodel j. If the number of rows exceeds numObs, then simulate uses the latest observations.

To use different predictors in each state, specify a cell vector of such matrices with length numStates.

By default, simulate ignores regression components in Mdl.

Data Types: double

Output Arguments

collapse all

`Y` — Simulated response paths
numeric matrix | numeric array

Simulated response paths, returned as a numeric matrix or array. Y represents the continuation of the presample responses in Y0.

For univariate ARX submodels, Y is a numObs-by-numPaths matrix. For multivariate VARX submodels, Y is a numObs-by-numSeries-by-numPaths array.

`E` — Simulated innovation paths
numeric matrix | numeric array

Simulated innovation paths, returned as a numeric matrix or array.

For univariate ARX submodels, E is a numObs-by-numPaths matrix. For multivariate VARX submodels, E is a numObs-by-numSeries-by-numPaths array.

simulate generates innovations using the covariance specification in Mdl. For more details, see tsVAR.

`StatePaths` — Simulated state paths
numeric matrix

Simulated state paths, returned as a numObs-by-numPaths numeric matrix.

If threshold levels in Mdl.Switch.Levels are t₁, t₂,… ,t_n, simulate labels states of the threshold variable (-∞,t₁), [t₁,t₂), … [t_n,∞) as 1, 2, 3,... n + 1, respectively.

References

[1] Teräsvirta, Tima. "Modelling Economic Relationships with Smooth Transition Regressions." In A. Ullahand and D.E.A. Giles (eds.), Handbook of Applied Economic Statistics, 507–552. New York: Marcel Dekker, 1998.

[2] van Dijk, Dick. Smooth Transition Models: Extensions and Outlier Robust Inference. Rotterdam, Netherlands: Tinbergen Institute Research Series, 1999.

Version History

Introduced in R2021b

simulate

Syntax

Description

Examples

Simulate Response Path from SETAR Model

Simulate Multiple Paths

Return Innovations and States

Initialize Multivariate Model Simulation from Multiple Starting Conditions

Simulate Model Containing Exogenous Regression Component

Perform Monte Carlo Estimation

Input Arguments

`Mdl` — Fully specified threshold-switching dynamic regression model
`tsVAR` model object

`numObs` — Number of observations to generate
positive integer

Name-Value Arguments

`NumPaths` — Number of sample paths to generate
`1` (default) | positive integer

`Type` — Type of threshold variable data
`"endogenous"` (default) | `"exogenous"`

`Y0` — Presample response data
numeric matrix | numeric array

`Z` — Threshold variable data z_t
empty array (`[]`) (default) | numeric vector | numeric matrix

`Delay` — Threshold variable delay d in y_j,t−d
`1` (default) | positive integer

`Index` — Threshold variable index j in y_j,t−d
`1` (default) | scalar in `1:Mdl.NumSeries`

`S0` — Initial states
`1` (default) | numeric scalar | numeric vector

`X` — Predictor data
numeric matrix | cell vector of numeric matrices

Output Arguments

`Y` — Simulated response paths
numeric matrix | numeric array

`E` — Simulated innovation paths
numeric matrix | numeric array

`StatePaths` — Simulated state paths
numeric matrix

References

Version History

See Also

Objects

Functions

Topics

simulate

Syntax

Description

Examples

Simulate Response Path from SETAR Model

Simulate Multiple Paths

Return Innovations and States

Initialize Multivariate Model Simulation from Multiple Starting Conditions

Simulate Model Containing Exogenous Regression Component

Perform Monte Carlo Estimation

Input Arguments

Mdl — Fully specified threshold-switching dynamic regression model tsVAR model object

numObs — Number of observations to generate positive integer

Name-Value Arguments

NumPaths — Number of sample paths to generate 1 (default) | positive integer

Type — Type of threshold variable data "endogenous" (default) | "exogenous"

Y0 — Presample response data numeric matrix | numeric array

Z — Threshold variable data zt empty array ([]) (default) | numeric vector | numeric matrix

Delay — Threshold variable delay d in yj,t−d 1 (default) | positive integer

Index — Threshold variable index j in yj,t−d 1 (default) | scalar in 1:Mdl.NumSeries

S0 — Initial states 1 (default) | numeric scalar | numeric vector

X — Predictor data numeric matrix | cell vector of numeric matrices

Output Arguments

Y — Simulated response paths numeric matrix | numeric array

E — Simulated innovation paths numeric matrix | numeric array

StatePaths — Simulated state paths numeric matrix

References

Version History

See Also

Objects

Functions

Topics

`Mdl` — Fully specified threshold-switching dynamic regression model
`tsVAR` model object

`numObs` — Number of observations to generate
positive integer

`NumPaths` — Number of sample paths to generate
`1` (default) | positive integer

`Type` — Type of threshold variable data
`"endogenous"` (default) | `"exogenous"`

`Y0` — Presample response data
numeric matrix | numeric array

`Z` — Threshold variable data z_t
empty array (`[]`) (default) | numeric vector | numeric matrix

`Delay` — Threshold variable delay d in y_j,t−d
`1` (default) | positive integer

`Index` — Threshold variable index j in y_j,t−d
`1` (default) | scalar in `1:Mdl.NumSeries`

`S0` — Initial states
`1` (default) | numeric scalar | numeric vector

`X` — Predictor data
numeric matrix | cell vector of numeric matrices

`Y` — Simulated response paths
numeric matrix | numeric array

`E` — Simulated innovation paths
numeric matrix | numeric array

`StatePaths` — Simulated state paths
numeric matrix