Algorithms to Determine Fixed-Point Types for Real Q-less QR Matrix Solve A'AX=B

Overview

You can solve the fixed-point matrix equation $$A^{\prime }AX=B$$ using QR decomposition. Using a sequence of orthogonal transformations, QR decomposition transforms matrix $$A$$ in-place to upper triangular $$R$$, where $$QR=A$$ is the economy-size QR decomposition. This reduces the equation to an upper-triangular system of equations $$R^{\prime }RX=B$$. To solve for $$X$$, compute $$X=R\backslash (R^{\prime }\backslash B)$$ through forward- and backward-substitution of $$R$$ into $$B$$.

You can determine appropriate fixed-point types for the matrix equation $$A^{\prime }AX=B$$ by selecting the fraction length based on the number of bits of precision defined by your requirements. The fixed.realQlessQRMatrixSolveFixedpointTypes function analytically computes the following upper bounds on $$R$$, and $$X$$ to determine the number of integer bits required to avoid overflow [1,2,3].

The upper bound for the magnitude of the elements of $$R=Q^{\prime }A$$ is

$$\max (|R(:)|)\le \sqrt{m}\max (|A(:)|)$$.

The upper bound for the magnitude of the elements of $$X=(A^{\prime }A)\backslash B$$ is

$$\max (|X(:)|)\le \frac{\sqrt{n}\max (|B(:)|)}{\min (\text{svd}(A){)}^2}$$.

Since computing $$\text{svd}(A)$$ is more computationally expensive than solving the system of equations, the fixed.realQlessQRMatrixSolveFixedpointTypes function estimates a lower bound of $$\min (\text{svd}(A))$$.

Fixed-point types for the solution of the matrix equation $$(A^{\prime }A)X=B$$ are generally well-bounded if the number of rows, $$m$$, of $$A$$ are much greater than the number of columns, $$n$$ (i.e. $$m\gg n$$), and $$A$$ is full rank. If $$A$$ is not inherently full rank, then it can be made so by adding random noise. Random noise naturally occurs in physical systems, such as thermal noise in radar or communications systems. If $$m=n$$, then the dynamic range of the system can be unbounded, for example in the scalar equation $$x=a^2/b$$ and $$a,b\in [-1,1]$$, then $$x$$ can be arbitrarily large if $$b$$ is close to $$0$$.

Proofs of the Bounds

Properties and Definitions of Vector and Matrix Norms

The proofs of the bounds use the following properties and definitions of matrix and vector norms, where $$Q$$ is an orthogonal matrix, and $$v$$ is a vector of length $$m$$ [6].

If $$A$$ is an $$m$$-by-$$n$$ matrix and $$QR=A$$ is the economy-size QR decomposition of $$A$$, where $$Q$$ is orthogonal and $$m$$-by-$$n$$ and $$R$$ is upper-triangular and $$n$$-by-$$n$$, then the singular values of $$R$$ are equal to the singular values of $$A$$. If $$A$$ is nonsingular, then

Upper Bound for R = Q'A

The upper bound for the magnitude of the elements of $$R$$ is

$$\max (|R(:)|)\le \sqrt{m}\max (|A(:)|)$$.

Proof of Upper Bound for R = Q'A

The $$j$$th column of $$R$$ is equal to $$R(:,j)=Q^{\prime }A(:,j)$$, so

Since $$\max (|R(:,j)|)\le \sqrt{m}\max (|A(:)|)$$ for all $$1\le j$$, then

Upper Bound for X = (A'A)\B

The upper bound for the magnitude of the elements of $$X=(A^{\prime }A)\backslash B$$ is

$$\max (|X(:)|)\le \frac{\sqrt{n}\max (|B(:)|)}{\min (\text{svd}(A){)}^2}$$.

Proof of Upper Bound for X = (A'A)\B

If $$A$$ is not full rank, then $$\min (\text{svd}(A))=0$$, and if $$B$$ is not equal to zero, then $$\sqrt{n}\max (|B(:)|)/\min (\text{svd}(A){)}^2=\infty$$and so the inequality is true.

If $$A^{\prime }Ax=b$$ and $$QR=A$$ is the economy-size QR decomposition of $$A$$, then $$A^{\prime }Ax=R^{\prime }{Q}^{\prime }QRx=R^{\prime }Rx=b$$. If $$A$$ is full rank then $$x=R^{-1}\cdot ((R^{\prime }{)}^{-1}b)$$. Let $$x=X(:,j)$$ be the $$j$$th column of $$X$$, and $$b=B(:,j)$$ be the $$j$$th column of $$B$$. Then

Since $$\max (|x(:)|)\le \sqrt{n}\max (|b(:)|)/\min (\text{svd}(A){)}^2$$ for all rows and columns of $$B$$ and $$X$$, then

$$\max (|X(:)|)\le \frac{\sqrt{n}\max (|B(:)|)}{\min (\text{svd}(A){)}^2}$$.

Lower Bound for min(svd(A))

You can estimate a lower bound $$s$$ of $$\min (\text{svd}(A))$$for real-valued $$A$$ using the following formula,

where $${\sigma }_N$$ is the standard deviation of random noise added to the elements of $$A$$, $$1-p_s$$ is the probability that $$s\le \min (\text{svd}(A))$$, $$\Gamma$$ is the gamma function, and $${\gamma }^{-1}$$is the inverse incomplete gamma function gammaincinv.

The proof is found in [1]. It is derived by integrating the formula in Lemma 3.3 from [3] and rearranging terms.

Since $$s\le \min (\text{svd}(A))$$ with probability $$1-p_s$$, then you can bound the magnitude of the elements of $$X$$ without computing $$\text{svd}(A)$$,

$$\max (|X(:)|)\le \frac{\sqrt{n}\max (|B(:)|)}{\min (\text{svd}(A){)}^2}\le \frac{\sqrt{n}\max (|B(:)|)}{s^2}$$ with probability $$1-p_s$$.

You can compute $$s$$ using the fixed.realSingularValueLowerBound function which uses a default probability of 5 standard deviations below the mean, $$p_s=(1+\text{erf}(-5/\sqrt{2}))/2\approx 2.8665\cdot 10^{-7}$$, so the probability that the estimated bound for the smallest singular value $$s$$ is less than the actual smallest singular value of $$A$$ is $$1-p_s\approx 0.9999997$$.

Example

This example runs a simulation with many random matrices and compares the analytical bounds with the actual singular values of $$A$$ and the actual largest elements of $$R=Q^{\prime }A$$, and $$X=(A^{\prime }A)\backslash B$$.

Define System Parameters

Define the matrix attributes and system parameters for this example.

m is the number of rows in matrix A. In a problem such as beamforming or direction finding, m corresponds to the number of samples that are integrated over.

m = 300;

n is the number of columns in matrix A and rows in matrices B and X. In a least-squares problem, m is greater than n, and usually m is much larger than n. In a problem such as beamforming or direction finding, n corresponds to the number of sensors.

n = 10;

p is the number of columns in matrices B and X. It corresponds to simultaneously solving a system with p right-hand sides.

p = 1;

In this example, set the rank of matrix A to be less than the number of columns. In a problem such as beamforming or direction finding, $$\text{rank}(A)$$ corresponds to the number of signals impinging on the sensor array.

rankA = 3;

precisionBits defines the number of bits of precision required for the matrix solve. Set this value according to system requirements.

precisionBits = 24;

In this example, real-valued matrices A and B are constructed such that the magnitude of their elements is less than or equal to one. Your own system requirements will define what those values are. If you don't know what they are, and A and B are fixed-point inputs to the system, then you can use the upperbound function to determine the upper bounds of the fixed-point types of A and B.

max_abs_A is an upper bound on the maximum magnitude element of A.

max_abs_A = 1;  

max_abs_B is an upper bound on the maximum magnitude element of B.

max_abs_B = 1;

Thermal noise standard deviation is the square root of thermal noise power, which is a system parameter. A well-designed system has the quantization level lower than the thermal noise. Here, set thermalNoiseStandardDeviation to the equivalent of $$-50$$dB noise power.

thermalNoiseStandardDeviation = sqrt(10^(-50/10))

thermalNoiseStandardDeviation = 
0.0032

The standard deviation of the noise from quantizing a real signal is $$2^{-\text{precisionBits}}/\sqrt{12}$$ [4,5]. Use fixed.realQuantizationNoiseStandardDeviation to compute this. See that it is less than thermalNoiseStandardDeviation.

quantizationNoiseStandardDeviation = fixed.realQuantizationNoiseStandardDeviation(precisionBits)

quantizationNoiseStandardDeviation = 
1.7206e-08

Compute Fixed-Point Types

In this example, assume that the designed system matrix $$A$$ does not have full rank (there are fewer signals of interest than number of columns of matrix $$A$$), and the measured system matrix $$A$$ has additive thermal noise that is larger than the quantization noise. The additive noise makes the measured matrix $$A$$ have full rank.

Set $${\sigma }_{\text{noise}}={\sigma }_{\text{thermal}\text{noise}}$$.

noiseStandardDeviation = thermalNoiseStandardDeviation;

Use fixed.realQlessQRMatrixSolveFixedpointTypes to compute fixed-point types.

T = fixed.realQlessQRMatrixSolveFixedpointTypes(m,n,max_abs_A,max_abs_B,...
    precisionBits,noiseStandardDeviation)

T = struct with fields:
    A: [0x0 embedded.fi]
    B: [0x0 embedded.fi]
    X: [0x0 embedded.fi]

T.A is the type computed for transforming $\mathit{A}$ to $\mathit{R}$ in-place so that it does not overflow.

T.A

ans = 

[]

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 31
        FractionLength: 24

T.B is the type computed for B so that it does not overflow.

T.B

ans = 

[]

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 27
        FractionLength: 24

T.X is the type computed for the solution $$X=(A^{\prime }A)\backslash B$$ so that there is a low probability that it overflows.

T.X

ans = 

[]

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 24

Upper Bound for R

The upper bound for $$R$$ is computed using the formula $$\max (|R(:)|)\le \sqrt{m}\max (|A(:)|)$$, where $$m$$ is the number of rows of matrix $$A$$. This upper bound is used to select a fixed-point type with the required number of bits of precision to avoid an overflow in the upper bound.

upperBoundR = sqrt(m)*max_abs_A

upperBoundR = 
17.3205

Lower Bound for min(svd(A)) for Real A

A lower bound for $$\min (\text{svd}(A))$$ is estimated by the fixed.realSingularValueLowerBound function using a probability that the estimate $$s$$ is not greater than the actual smallest singular value. The default probability is 5 standard deviations below the mean. You can change this probability by specifying it as the last input parameter to the fixed.realSingularValueLowerBound function.

estimatedSingularValueLowerBound = fixed.realSingularValueLowerBound(m,n,noiseStandardDeviation)

estimatedSingularValueLowerBound = 
0.0371

Simulate and Compare to the Computed Bounds

The bounds are within an order of magnitude of the simulated results. This is sufficient because the number of bits translates to a logarithmic scale relative to the range of values. Being within a factor of 10 is between 3 and 4 bits. This is a good starting point for specifying a fixed-point type. If you run the simulation for more samples, then it is more likely that the simulated results will be closer to the bound. This example uses a limited number of simulations so it doesn't take too long to run. For real-world system design, you should run additional simulations.

Define the number of samples, numSamples, over which to run the simulation.

numSamples = 1e4;

Run the simulation.

[actualMaxR,singularValues,X_values] = runSimulations(m,n,p,rankA,max_abs_A,max_abs_B,numSamples,...
    noiseStandardDeviation,T);

You can see that the upper bound on $$R$$ compared to the measured simulation results of the maximum value of $$R$$ over all runs is within an order of magnitude.

upperBoundR

upperBoundR = 
17.3205

max(actualMaxR)

ans = 
8.1682

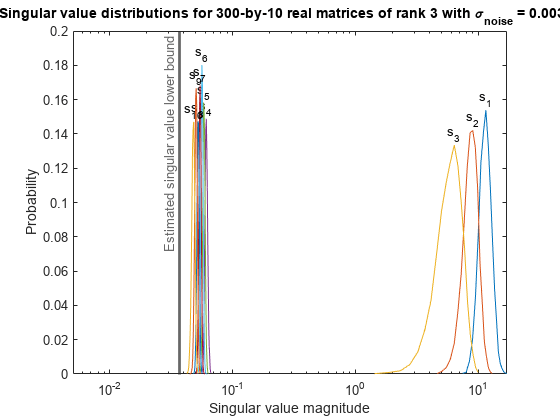
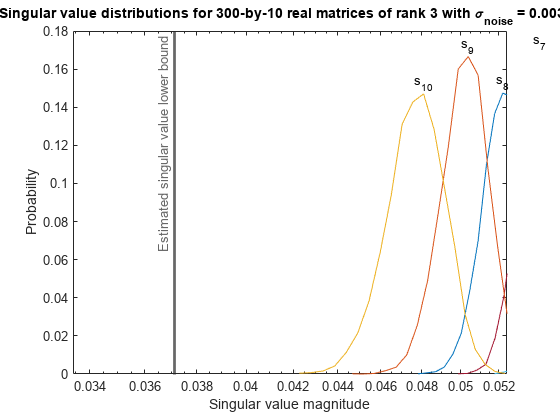
Finally, see that the estimated lower bound of $$\min (\text{svd}(A))$$ compared to the measured simulation results of $$\min (\text{svd}(A))$$ over all runs is also within an order of magnitude.

estimatedSingularValueLowerBound

estimatedSingularValueLowerBound = 
0.0371

actualSmallestSingularValue = min(singularValues,[],'all')

actualSmallestSingularValue = 
0.0421

Plot the distribution of the singular values over all simulation runs. The distributions of the largest singular values correspond to the signals that determine the rank of the matrix. The distributions of the smallest singular values correspond to the noise. The derivation of the estimated bound of the smallest singular value makes use of the random nature of the noise.

clf
fixed.example.plot.singularValueDistribution(m,n,rankA,...
    noiseStandardDeviation,singularValues,...
    estimatedSingularValueLowerBound,"real");

Zoom in to the smallest singular value to see that the estimated bound is close to it.

xlim([estimatedSingularValueLowerBound*0.9, max(singularValues(n,:))]);

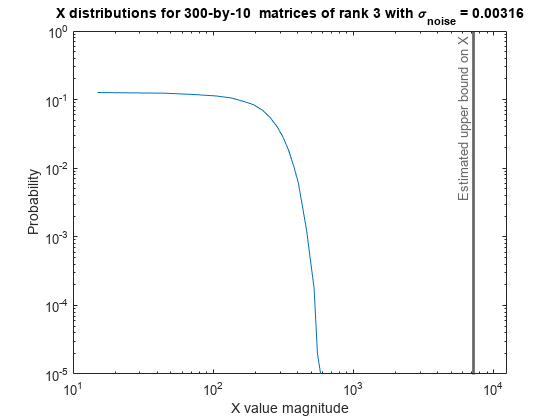
Estimate the largest value of the solution, X, and compare it to the largest value of X found during the simulation runs. The estimation is within an order of magnitude of the actual value, which is sufficient for estimating a fixed-point data type, because it is between 3 and 4 bits.

This example uses a limited number of simulation runs. With additional simulation runs, the actual largest value of X will approach the estimated largest value of X.

estimated_largest_X = fixed.realQlessQRMatrixSolveUpperBoundX(m,n,max_abs_B,noiseStandardDeviation)

estimated_largest_X = 
7.2565e+03

actual_largest_X = max(abs(X_values),[],'all')

actual_largest_X = 
582.6761

Plot the distribution of X values and compare it to the estimated upper bound for X.

clf
fixed.example.plot.xValueDistribution(m,n,rankA,noiseStandardDeviation,...
    X_values,estimated_largest_X,"real normally distributed random");

Supporting Functions

The runSimulations function creates a series of random matrices $$A$$ and $$B$$ of a given size and rank, quantizes them according to the computed types, computes the QR decomposition of $$A$$, and solves the equation $$A^{\prime }AX=B$$. It returns the maximum values of $$R=Q^{\prime }A$$, the singular values of $$A$$, and the values of $$X$$ so their distributions can be plotted and compared to the bounds.

function [actualMaxR,singularValues,X_values] = runSimulations(m,n,p,rankA,max_abs_A,max_abs_B,...
        numSamples,noiseStandardDeviation,T)
    precisionBits = T.A.FractionLength;
    A_WordLength = T.A.WordLength;
    B_WordLength = T.B.WordLength;
    actualMaxR = zeros(1,numSamples);
    singularValues = zeros(n,numSamples);
    X_values = zeros(n,numSamples);
    for j = 1:numSamples
        A = max_abs_A*fixed.example.realRandomLowRankMatrix(m,n,rankA);
        % Adding random noise makes A non-singular.
        A = A + fixed.example.realNormalRandomArray(0,noiseStandardDeviation,m,n);
        A = quantizenumeric(A,1,A_WordLength,precisionBits);
        B = fixed.example.realUniformRandomArray(-max_abs_B,max_abs_B,n,p);
        B = quantizenumeric(B,1,B_WordLength,precisionBits);
        [~,R] = qr(A,0);
        X = R\(R'\B);
        actualMaxR(j) = max(abs(R(:)));
        singularValues(:,j) = svd(A);
        X_values(:,j) = X;
    end
end

References

Suppress mlint warnings in this file.

%#ok<*NASGU>
%#ok<*ASGLU>