accelcal

Calibration parameters for accelerometer

Since R2023b

Syntax

[A,b] = accelcal(D)

[A,b] = accelcal(XUP,XDOWN,YUP,YDOWN,ZUP,ZDOWN)

[A,b] = accelcal(___,Gravity=g)

Description

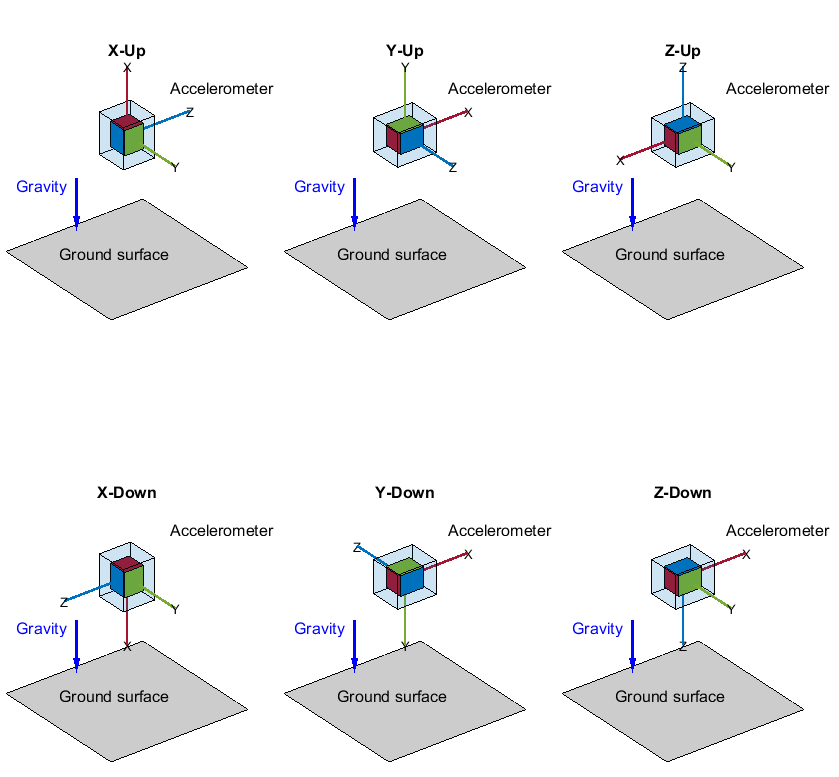
[A,b] = accelcal(D) returns matrix A and vector b used to correct uncalibrated accelerometer measurements based on the calibration data D.

After obtaining A and b, obtain the calibrated data C from uncalibrated data U by using C = U*A + b, where U is a M-by-3 matrix and each row of U is an uncalibrated accelerometer measurement.

example

[A,b] = accelcal(XUP,XDOWN,YUP,YDOWN,ZUP,ZDOWN) specifies the measurement data at six calibration orientations as shown in Accelerometer Calibration Orientations.

[A,b] = accelcal(___,Gravity=g) specifies the value of the Earth gravity constant g.

Examples

collapse all

Calibrate Accelerometer Measurements

Open Live Script

Create an imuSensor object for generating measurement data. By default, the reference frame of the object is the north-east-down (NED) frame. Specify the accelerometer parameters so that the measurements contain a constant bias and some random noise.

accelParams =  accelparams(ConstantBias=[.1 .2 -.1],...
    NoiseDensity=1e-2*ones(1,3));
imu = imuSensor(Accelerometer=accelParams);
disp(imu.ReferenceFrame)

NED

Define the Euler angles for six calibration orientations and convert them to quaternions.

orients = [...
    0 90 0 % xUp
    0 0 -90 % yUp
    0 180 0 % zUp
    0 -90 0 % xDown 
    0 0 90 % yDown    
    0 0 0]; % zDown
quats = quaternion(orients,"eulerd","ZYX","frame");
N = numel(quats);

Assume the external accelerations and angular velocities are both 0. Simulate the IMU sensor to get the calibration measurements.

exAcc = zeros(N,3);
angVel = zeros(N,3);
D = imu(exAcc,angVel,quats)

D = 6×3

   -9.6490    0.2225   -0.1925
    0.0146   -9.5593    0.0153
   -0.0210    0.1928   -9.9271
    9.9363    0.1840   -0.0210
    0.0008    9.9094   -0.0655
    0.2828    0.1528    9.7232

Use the accelcal function to obtain the calibration parameters.

[A,b] = accelcal(D)

A = 3×3

    1.0018    0.0019   -0.0087
    0.0006    1.0078    0.0041
   -0.0154    0.0020    0.9986

b = 1×3

   -0.0956   -0.1852    0.0779

Verify the calibration parameters by using the calibration measurements.

DCali = D*A+b

DCali = 6×3

   -9.7587    0.0199   -0.0298
   -0.0872   -9.8187    0.0534
    0.0365   -0.0111   -9.8339
    9.8589    0.0196   -0.0284
   -0.0875    9.8012    0.0535
    0.0380   -0.0109    9.7852

Create some random orientations, obtain the accelerometer measurements, and calibrate the measurements.

M = 10;
randomQuats = randrot(M,1);
U = imu(zeros(M,3),zeros(M,3),randomQuats);
C = U*A+b

C = 10×3

    9.1400    3.5374   -1.3008
   -7.1185   -6.8126   -0.7088
    7.1372   -6.8065   -0.5943
   -7.9362    1.5605    5.6203
    7.4397   -2.3143   -6.2363
    7.0758   -4.0794   -5.7321
    3.1250   -5.4306    7.2655
    0.8261   -9.7286    1.3509
    0.8486    2.8606   -9.2705
   -2.4922    8.5000   -3.9532

Input Arguments

collapse all

`D` — Measurements at six calibration orientations
N-by-3 matrix

Measurements at the six calibration orientations of the accelerometer, specified as an N-by-3 matrix. N is the total number of measurements. Each row of the matrix is a measurement at one of the six calibration orientations of the accelerometer, as shown in Accelerometer Calibration Orientations. For best results, the matrix should contain an equal number of measurements for all the six orientations.

When interpreting the data in D, the function by default assumes that the Earth gravity constant g is 9.81m/s² or 1, whichever is closer to the mean of the norm of the data.