使用遗传算法进行约束最小化
此示例说明如何使用遗传算法最小化受非线性不等式约束和边界的目标函数。
约束最小化问题
对于这个问题,要最小化的目标函数是二维变量 x 的简单函数。
simple_objective(x) = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
该函数被称为 "cam",如 LCW Dixon 和 GP Szego [1] 中所述。
此外,该问题具有非线性约束和边界。
x(1)*x(2) + x(1) - x(2) + 1.5 <= 0 (nonlinear constraint) 10 - x(1)*x(2) <= 0 (nonlinear constraint) 0 <= x(1) <= 1 (bound) 0 <= x(2) <= 13 (bound)
编写适应度函数代码
创建一个名为 simple_objective.m 的 MATLAB 文件,其中包含以下代码:
type simple_objectivefunction y = simple_objective(x) %SIMPLE_OBJECTIVE Objective function for PATTERNSEARCH solver % Copyright 2004 The MathWorks, Inc. x1 = x(1); x2 = x(2); y = (4-2.1.*x1.^2+x1.^4./3).*x1.^2+x1.*x2+(-4+4.*x2.^2).*x2.^2;
诸如 ga 之类的求解器接受单个输入 x,其中 x 的元素数量与问题中的变量数量一样多。目标函数计算目标函数的标量值并在其单个输出参量 y 中返回它。
编写约束函数
创建一个名为 simple_constraint.m 的 MATLAB 文件,其中包含以下代码:
type simple_constraintfunction [c, ceq] = simple_constraint(x)
%SIMPLE_CONSTRAINT Nonlinear inequality constraints.
% Copyright 2005-2007 The MathWorks, Inc.
c = [1.5 + x(1)*x(2) + x(1) - x(2);
-x(1)*x(2) + 10];
% No nonlinear equality constraints:
ceq = [];
约束函数计算所有不等式和等式约束的值,并分别返回向量 c 和 ceq。c 的值表示求解器试图使其小于或等于零的非线性不等式约束。ceq 的值表示求解器试图使其等于零的非线性等式约束。这个例子没有非线性等式约束,所以 ceq = []。有关详细信息,请参阅非线性约束。
使用 ga 进行最小化
将目标函数指定为函数句柄。
ObjectiveFunction = @simple_objective;
指定问题边界。
lb = [0 0]; % Lower bounds ub = [1 13]; % Upper bounds
将非线性约束函数指定为函数句柄。
ConstraintFunction = @simple_constraint;
指定问题变量的数量。
nvars = 2;
调用求解器,请求最优点 x 和最优点 fval 处的函数值。
rng default % For reproducibility [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub,ConstraintFunction)
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
添加可视化
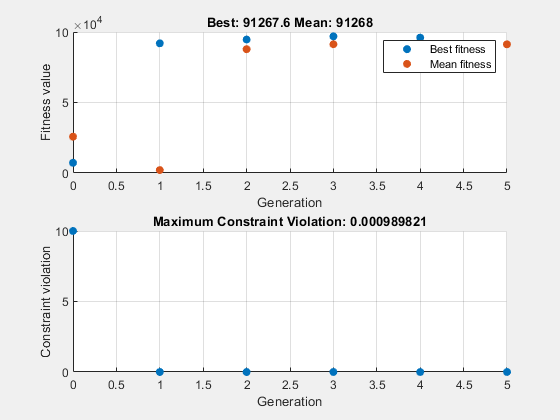
要观察求解器的进度,请指定选择两个绘图函数的选项。绘图函数 gaplotbestf 绘制每次迭代中的最佳目标函数值,绘图函数 gaplotmaxconstr 绘制每次迭代中的最大约束违反。在元胞数组中设置这两个绘图函数。另外,通过将 Display 选项设置为 'iter',在命令窗口中显示有关求解器进度的信息。
options = optimoptions("ga",'PlotFcn',{@gaplotbestf,@gaplotmaxconstr}, ... 'Display','iter');
运行求解器,包括 options 参量。
[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ...
ConstraintFunction,options)Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2524 91986.8 7.786e-09 0
2 4986 94677.4 0 0
3 10362 96929.2 0 0
4 16067 96006.3 0 0
5 23405 91267.6 0.0009898 0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
通过迭代显示,ga 提供了有关问题类型以及创建、交叉、变异和选择运算符的详细信息。
非线性约束导致 ga 在每次迭代时解决许多子问题。从绘图和迭代显示可以看出,解过程只有几次迭代。但是,迭代显示中的 Func-count 列显示每次迭代有许多函数计算。
ga 求解器处理线性约束和边界与处理非线性约束的方式不同。在整个优化过程中,所有线性约束和边界都得到满足。然而,ga 可能不会在每代都满足所有非线性约束。如果 ga 收敛到一个解,则非线性约束将在该解得到满足。
ga 使用突变和交叉函数在每一代产生新的个体。ga 满足线性和边界约束的方式是使用仅生成可行点的变异和交叉函数。例如,在之前对 ga 的调用中,默认变异函数(对于无约束问题)mutationgaussian 不满足线性约束,因此 ga 默认使用 mutationadaptfeasible 函数。如果您提供自定义变异函数,则该自定义函数必须仅生成相对于线性和边界约束可行的点。工具箱中的所有交叉函数都会生成满足线性约束和边界的点。
但是,当您的问题包含整数约束时,ga 会强制所有迭代满足边界和线性约束。这种可行性对于所有的变异、交叉和创建操作都存在,并且在一个很小的容差范围内。
提供起点
为了加快求解器的速度,您可以在 InitialPopulationMatrix 选项中提供初始种群。ga 使用初始种群来开始优化。指定一个行向量或矩阵,其中每行代表一个起点。
X0 = [0.8 12.5]; % Start point (row vector) options.InitialPopulationMatrix = X0; [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ... ConstraintFunction,options)
Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2500 91507.4 0 0
2 4950 91270.4 0.0009621 0
3 7400 91270.4 0.0009621 1
4 9850 91269.2 0.0009958 0
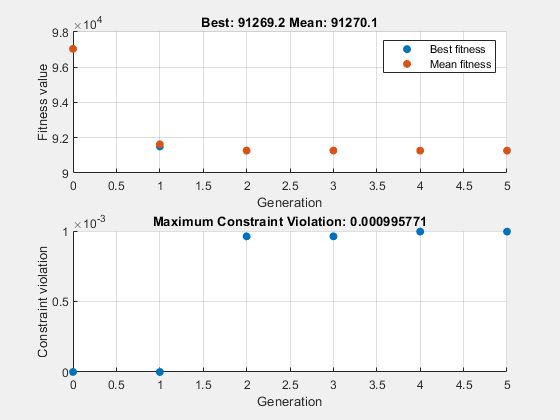
5 12300 91269.2 0.0009958 1
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
0.8122 12.3104
fval = 9.1269e+04
在这种情况下,提供起点不会实质性地改变求解器的进度。
参考资料
[1] Dixon, L. C. W., and G .P. Szego (eds.).Towards Global Optimisation 2.North-Holland:Elsevier Science Ltd., Amsterdam, 1978.