仅使用可行的起点进行优化

您可以设置 StartPointsToRun 选项，以便 MultiStart 和 GlobalSearch 仅使用满足不等式约束的起点。由于局部求解器不必搜索可行区域，因此此选项可以加速您的优化。然而，该选项可能会导致求解器错过一些吸引盆。

StartPointsToRun 选项有三种设置：

all - 接受所有起点
bounds - 拒绝不满足边界的起点
bounds-ineqs - 拒绝不满足边界或不等式约束的起点

例如，假设您的目标函数是

function y = tiltcircle(x)
vx = x(:)-[4;4]; % ensure vx is in column form
y = vx'*[1;1] + sqrt(16 - vx'*vx); % complex if norm(x-[4;4])>4

tiltcircle 为 norm(x - [4 4]) > 4 返回复数值。

用于生成图窗的代码

编写一个约束函数，该函数在集合上为正，其中 norm(x - [4 4]) > 4

function [c ceq] = myconstraint(x)
ceq = [];
cx = x(:) - [4;4]; % ensure x is a column vector
c = cx'*cx - 16; % negative where tiltcircle(x) is real

设置 GlobalSearch 仅使用满足不等式约束的起点：

gs = GlobalSearch('StartPointsToRun','bounds-ineqs');

为了完成示例，请创建一个问题结构体并运行求解器：

opts = optimoptions(@fmincon,'Algorithm','interior-point');
problem = createOptimProblem('fmincon',...
    'x0',[4 4],'objective',@tiltcircle,...
    'nonlcon',@myconstraint,'lb',[-10 -10],...
    'ub',[10 10],'options',opts);
rng(7,'twister'); % for reproducibility
[x,fval,exitflag,output,solutionset] = run(gs,problem)

GlobalSearch stopped because it analyzed all the trial points.

All 5 local solver runs converged with a positive local solver exit flag.

x =

    1.1716    1.1716


fval =

   -5.6530


exitflag =

     1


output =

  struct with fields:

                funcCount: 3242
         localSolverTotal: 5
       localSolverSuccess: 5
    localSolverIncomplete: 0
    localSolverNoSolution: 0
                  message: 'GlobalSearch stopped because it analyzed all the trial po...'

solutionset = 

  1x4 GlobalOptimSolution array with properties:

    X
    Fval
    Exitflag
    Output
    X0

具有局部最小值的 tiltcircle

用于生成图窗的代码

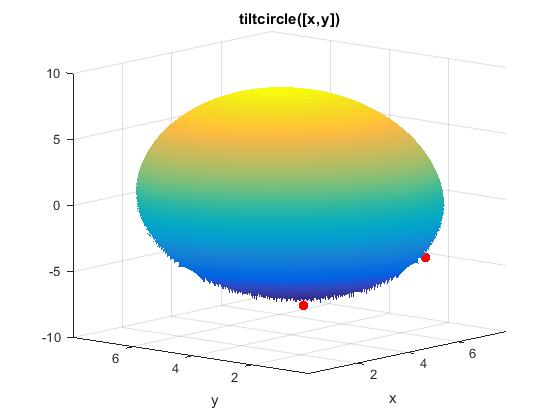
tiltcircle 函数只有一个局部最小值。然而 GlobalSearch (fmincon) 在几个点处停止了。这是否意味着 fmincon 犯了错误？

fmincon 在几个边界点停止的原因很微妙。tiltcircle 函数在边界上具有无限的梯度，从一维计算可以看出：

$\frac{d}{d x} \sqrt{16 - x^{2}} = \frac{- x}{\sqrt{16 - x^{2}}} = \pm \infty at | x | = 4.$

因此在边界的法线上存在巨大的梯度。该梯度压倒了线性项产生的微小额外倾斜。据 fmincon 所知，边界点是约束问题的驻点。

只要函数有平方根，就会出现这种行为。

仅使用可行的起点进行优化

另请参阅

主题