求解器处理非光滑问题的行为
这个例子说明了为优化问题选择合适的求解器的重要性。它还表明,单点的不平滑可能会给 Optimization Toolbox™ 求解器带来问题。
一般来说,求解器决策表可为您提供指导,帮助您选择最适合您问题的求解器。对于平滑问题,请请参阅 优化决策表。对于非平滑问题,请首先参阅 选择求解器的表格,有关更多信息,请参阅 Global Optimization Toolbox 求解器特性。
具有单个非光滑点的函数
函数 在点 0 处不光滑,该点即为最小点。下面是使用矩阵范数对四维点 绘制的二维图。
figure x = linspace(-5,5,51); [xx,yy] = meshgrid(x); zz = zeros(size(xx)); for ii = 1:length(x) for jj = 1:length(x) zz(ii,jj) = sqrt(norm([xx(ii,jj),yy(ii,jj);0,0])); end end surf(xx,yy,zz) xlabel('x(1)') ylabel('x(2)') title('Norm([x(1),x(2);0,0])^{1/2}')
![Figure contains an axes object. The axes object with title Norm([x( 1 ),x( 2 ); 0 , 0 ]) toThePowerOf 1 / 2 baseline, xlabel x(1), ylabel x(2) contains an object of type surface.](../examples/globaloptim/win64/SolverPerformanceWithANonsmoothProblemExample_01.png)
此示例对 2×6 矩阵 x 使用矩阵范数。矩阵范数与奇异值分解有关,它不像欧几里得范数那样平滑。请参阅 矩阵的 2-范数。
尽量减少使用 patternsearch
对于非平滑问题,建议首先尝试使用 patternsearch 求解器。请参阅 选择求解器的表格。从非零的 2×6 矩阵 patternsearch 开始 x0,并尝试找到 的最小值。对于此次尝试以及所有其他尝试,请使用默认求解器选项。
返回应接近于零的解、同样应接近于零的目标函数值以及所进行的函数计算的次数。
fun = @(x)norm([x(1:6);x(7:12)])^(1/2);
x0 = [1:6;7:12];
rng default
x0 = x0 + rand(size(x0))x0 = 2×6
1.8147 2.1270 3.6324 4.2785 5.9575 6.1576
7.9058 8.9134 9.0975 10.5469 11.9649 12.9706
[xps,fvalps,eflagps,outputps] = patternsearch(fun,x0);
patternsearch stopped because the mesh size was less than options.MeshTolerance.
xps,fvalps,eflagps,outputps.funccount
xps = 2×6
10-4 ×
0.1116 -0.1209 0.3503 -0.0520 -0.1270 0.2031
-0.3082 -0.1526 0.0623 0.0652 0.4479 0.1173
fvalps = 0.0073
eflagps = 1
ans = 10780
patternsearch 达到了一个好的解,如退出标志 1 所示。然而,它需要超过 10,000 次函数计算才能收敛。
尽量减少使用 fminsearch
文档指出 fminsearch 有时可以处理不连续性,因此这是一个合理的选择。
[xfms,fvalfms,eflagfms,outputfms] = fminsearch(fun,x0);
Exiting: Maximum number of function evaluations has been exceeded
- increase MaxFunEvals option.
Current function value: 3.197063
xfms,fvalfms,eflagfms,outputfms.funcCount
xfms = 2×6
2.2640 1.1747 9.0693 8.1652 1.7367 -1.2958
3.7456 1.2694 0.2714 -3.7942 3.8714 1.9290
fvalfms = 3.1971
eflagfms = 0
ans = 2401
使用默认选项,fminsearch 在收敛到解之前会用尽函数计算。退出标志 0 表示缺乏收敛。所报告的解很差。
使用 particleswarm
建议尝试使用 particleswarm 作为下一个求解器。请参阅 选择非光滑问题求解器。
[xpsw,fvalpsw,eflagpsw,outputpsw] = particleswarm(fun,12);
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
xpsw,fvalpsw,eflagpsw,outputpsw.funccount
xpsw = 1×12
10-12 ×
-0.0386 -0.1282 -0.0560 0.0904 0.0771 -0.0541 -0.1189 0.1290 -0.0032 0.0165 0.0728 -0.0026
fvalpsw = 4.5222e-07
eflagpsw = 1
ans = 37200
particleswarm 找到了比 patternsearch 更准确的解,但需要超过 35,000 次函数计算。退出标志 1 表示解是好的。
使用 ga
ga 是一种流行的求解器,但不建议作为第一个尝试的求解器。看看它解决这个问题的效果如何。
[xga,fvalga,eflagga,outputga] = ga(fun,12);
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
xga,fvalga,eflagga,outputga.funccount
xga = 1×12
-0.0061 -0.0904 0.0816 -0.0484 0.0799 -0.1925 0.0048 0.3581 0.0848 0.0232 0.0237 -0.1294
fvalga = 0.6257
eflagga = 1
ans = 65190
ga 找不到与 patternsearch 或 particleswarm 一样好的解,并且函数计算次数大约是 particleswarm 的两倍。在这种情况下,退出标志 1 具有误导性。
使用 Optimization Toolbox 中的 fminunc
不推荐将 fminunc 用于非平滑函数。看看这个的表现如何。
[xfmu,fvalfmu,eflagfmu,outputfmu] = fminunc(fun,x0);
Local minimum possible. fminunc stopped because the size of the current step is less than the value of the step size tolerance. <stopping criteria details>
xfmu,fvalfmu,eflagfmu,outputfmu.funcCount
xfmu = 2×6
-0.5844 -0.9726 -0.4356 0.1467 0.3263 -0.1002
-0.0769 -0.1092 -0.3429 -0.6856 -0.7609 -0.6524
fvalfmu = 1.1269
eflagfmu = 2
ans = 429
fminunc 解不如 ga 解好。然而,fminunc 在相对较少的函数计算中就得出了相当差的解。退出标志 2 意味着您应该小心,报告的解不满足一阶最优条件。
使用 Optimization Toolbox 中的 fmincon
fmincon 有时可以最小化非光滑函数。看看这个的表现如何。
[xfmc,fvalfmc,eflagfmc,outputfmc] = fmincon(fun,x0);
Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
xfmc,fvalfmc,eflagfmc,outputfmc.funcCount
xfmc = 2×6
10-9 ×
0.0435 -0.0976 0.0756 -0.1265 0.0112 -0.0336
0.0634 0.0528 -0.0144 0.0957 0.1322 -0.1136
fvalfmc = 1.5501e-05
eflagfmc = 2
ans = 876
采用默认选项的 fmincon 在少于 1000 次函数计算后便可得出准确的解。退出标志 2 并不意味着解不准确,而是不满足一阶最优条件。这是因为目标函数的梯度在解不为零。
结果摘要
选择合适的求解器可以获得更好、更快的结果。此摘要显示了结果可能有多么不同。如果目标函数值大于 0.1,则解质量为 'Poor';如果目标函数值小于 0.01,则解质量为 'Good';否则,解质量为 'Mediocre'。
Solver = {'patternsearch';'fminsearch';'particleswarm';'ga';'fminunc';'fmincon'};
SolutionQuality = {'Good';'Poor';'Good';'Poor';'Poor';'Good'};
FVal = [fvalps,fvalfms,fvalpsw,fvalga,fvalfmu,fvalfmc]';
NumEval = [outputps.funccount,outputfms.funcCount,outputpsw.funccount,...
outputga.funccount,outputfmu.funcCount,outputfmc.funcCount]';
results = table(Solver,SolutionQuality,FVal,NumEval)results=6×4 table
Solver SolutionQuality FVal NumEval
_________________ _______________ __________ _______
{'patternsearch'} {'Good'} 0.0072656 10780
{'fminsearch' } {'Poor'} 3.1971 2401
{'particleswarm'} {'Good'} 4.5222e-07 37200
{'ga' } {'Poor'} 0.62572 65190
{'fminunc' } {'Poor'} 1.1269 429
{'fmincon' } {'Good'} 1.5501e-05 876
从另一个角度看结果。
figure hold on for ii = 1:length(FVal) clr = rand(1,3); plot(NumEval(ii),FVal(ii),'o','MarkerSize',10,'MarkerEdgeColor',clr,'MarkerFaceColor',clr) text(NumEval(ii),FVal(ii)+0.2,Solver{ii},'Color',clr); end ylabel('FVal') xlabel('NumEval') title('Reported Minimum and Evaluations By Solver') hold off
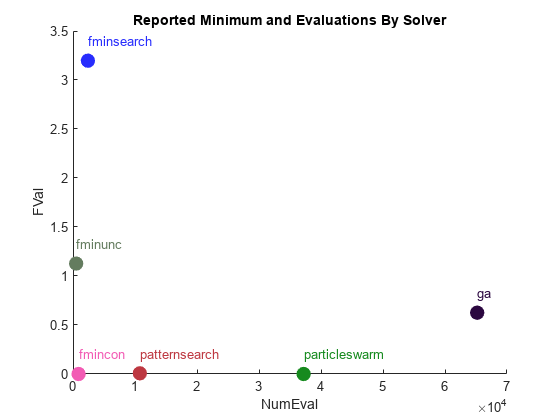
虽然 particleswarm 实现了最低的目标函数值,但它实现的函数计算次数是 patternsearch 的三倍多,是 fmincon 的 30 倍多。
对于非光滑问题,通常不建议使用 fmincon。在这种情况下它是有效的,但是这种情况只有一个非光滑点。