本页采用了机器翻译。点击此处可查看最新英文版本。

解决具有整数和非线性约束的非线性问题

打开实时脚本

surrogateopt 求解器同时接受整数约束和非线性约束。比较具有和不具有整数约束的非线性问题的解。整数约束使得解位于合理精细的网格上。

目标函数和约束函数

目标函数为

f(x)=log(1+3(x2-(x13-x1))2+(x1-4/3)2).

该目标函数是非负的，在点 x=[4/3,(4/3)3-4/3] = [1.3333, 1.0370] 处取最小值 0。

该问题有两个非线性约束函数。

x14≤5sinh(x2/5),x22≤5tanh(x1/5)+1.

绘制非线性约束的可行区域。

[X,Y] = meshgrid(-2:.01:3);
Z = (5*sinh(Y./5) >= X.^4); 
% Z=1 where the first constraint is satisfied, Z=0 otherwise
Z = Z+ 2*(5*tanh(X./5) >= Y.^2 - 1); 
% Z=2 where the second constraint is satisfied
% Z=3 where both constraints are satisfied
surf(X,Y,Z,'LineStyle','none');
fig = gcf;
fig.Color = 'w'; % white background
view(0,90)
xlabel('x_1')
ylabel('x_2')

Figure contains an axes object. The axes object with xlabel x indexOf 1 baseline x_1, ylabel x indexOf 2 baseline x_2 contains an object of type surface.

黄色区域显示两个约束均得到满足的地方。

surrogateopt 要求目标函数和约束函数是同一函数的一部分，即返回结构体的函数。目标函数位于结构体的 Fval 字段中，约束位于 Ineq 字段中。这些字段是本示例末尾的 objconstr 函数的输出。

将整数约束缩放至细网格上

将问题设置为在两个变量 x(1) 和 x(2) 中都有整数约束。

intcon = [1 2];

缩放问题，以便变量按 s = 1/10 缩放，其中 s 与变量相乘。

s = 0.1;
f = @(x)objconstr(x,s);

为了使此缩放有效，您需要将边界缩放 1/s。将未缩放的边界设置为 -2≤xi≤3，并将每个边界缩放至 1/s。

lb = [-2,-2]/s;
ub = [3,3]/s;

通过使用缩放 s，该问题实际上在每个分量 s 和 x(1) 中都有 x(2) 的间距。将整数点绘制为间距为 s 的网格。

hold on
grid on
ax = gca;
sp = -2:s:3;
ax.XTick = sp;
ax.YTick = sp;
ax.Layer = 'top';
ax.GridAlpha = 1/2;
ax.XTickLabel = '';
ax.YTickLabel = '';
xlabel('x_1')
ylabel('x_2')
hold off

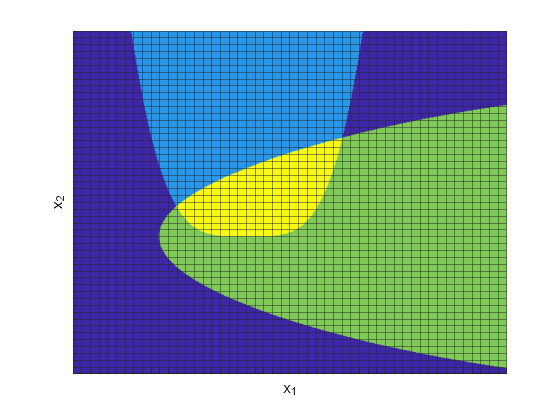
Figure contains an axes object. The axes object with xlabel x indexOf 1 baseline x_1, ylabel x indexOf 2 baseline x_2 contains an object of type surface.

解决扩展问题

设置选项以使用比默认值更严格的约束，并使用 surrogateoptplot 绘图函数。

opts = optimoptions('surrogateopt','PlotFcn',"surrogateoptplot","ConstraintTolerance",1e-6);

调用 surrogateopt 以求解问题。

rng default % For reproducibility
[sol,fval,eflag,outpt] = surrogateopt(f,lb,ub,intcon,opts)

Figure Optimization Plot Function contains an axes object. The axes object with title Best: 0.863447 Incumbent: 1.28024 Current: 1.28024, xlabel Number of Function Evaluations, ylabel Objective Function contains 11 objects of type line. One or more of the lines displays its values using only markers These objects represent Infeasible Best, Infeasible Incumbent, Infeasible Random Samples, Best, Incumbent, Random Samples, Infeasible Adaptive Samples, Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol = 1×2

     5     1


fval = 
0.8634

eflag = 
0

outpt = struct with fields:
        elapsedtime: 49.3411
          funccount: 200
    constrviolation: -0.0375
               ineq: [-0.0375 -1.4883]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

在图中将解绘制为红色圆圈。请注意，目标函数值约为 0.86。

figure(fig);
hold on
plot3(sol(1)*s,sol(2)*s,5,'ro')
hold off

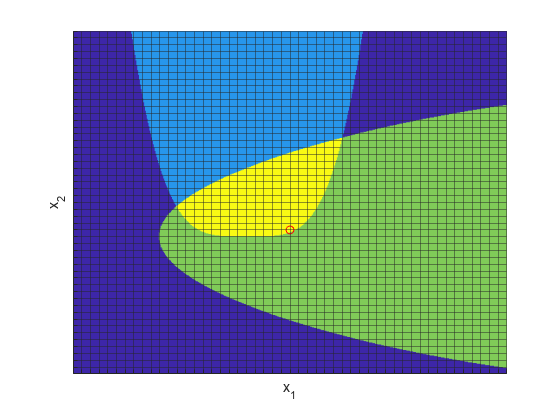
Figure contains an axes object. The axes object with xlabel x indexOf 1 baseline x_1, ylabel x indexOf 2 baseline x_2 contains 2 objects of type surface, line. One or more of the lines displays its values using only markers

与没有整数约束的解进行比较

将具有整数约束的解与不具有整数约束的解进行比较。

[sol2,fval2,eflag2,outpt2] = surrogateopt(f,lb,ub,[],opts)

Figure Optimization Plot Function contains an axes object. The axes object with title Best: 0.815261 Incumbent: 2.35107 Current: 3.49564, xlabel Number of Function Evaluations, ylabel Objective Function contains 10 objects of type line. One or more of the lines displays its values using only markers These objects represent Infeasible Best, Infeasible Incumbent, Infeasible Random Samples, Best, Incumbent, Random Samples, Adaptive Samples, Infeasible Adaptive Samples, Surrogate Reset.

surrogateopt stopped because it exceeded the function evaluation limit set by 
'options.MaxFunctionEvaluations'.

sol2 = 1×2

    4.3882    0.3709


fval2 = 
0.8153

eflag2 = 
0

outpt2 = struct with fields:
        elapsedtime: 33.5512
          funccount: 200
    constrviolation: -1.2426e-05
               ineq: [-1.2426e-05 -1.4363]
           rngstate: [1×1 struct]
            message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'

这里，目标函数值约为 0.815。整数约束使目标函数值增加不到 10%。绘制新解与前一个整数解。放大以更清楚地看到解点。

figure(fig)
hold on
plot3(sol2(1)*s,sol2(2)*s,5,'k*','MarkerSize',12)
xlim([0 1])
ylim([-1/2 1/2])
hold off

Figure contains an axes object. The axes object with xlabel x indexOf 1 baseline x_1, ylabel x indexOf 2 baseline x_2 contains 3 objects of type surface, line. One or more of the lines displays its values using only markers

辅助函数

以下代码创建 objconstr 辅助函数。该函数将变量 x 乘以因子 s，在 F 结构体的 Fval 字段中返回目标函数值，在 F 结构体的 Ineq 字段中返回非线性约束。

function F = objconstr(x,s)
x = x*s;
fun = log(1 + 3*(x(2) - (x(1)^3 - x(1)))^2 + (x(1) - 4/3)^2);
c1 = x(1)^4 - 5*sinh(x(2)/5);
c2 = x(2)^2 - 5*tanh(x(1)/5) - 1;
c = [c1 c2];
F.Fval = fun;
F.Ineq = c;
end

另请参阅

主题