使用自定义数据类型的模拟退火进行多处理器调度
此示例说明如何使用模拟退火来最小化使用自定义数据类型的函数。这里定制模拟退火来解决多处理器调度问题。
多处理器调度问题
多处理器调度问题包括在一组处理器上找到任务的最佳分配。给出了处理器的数量和任务的数量。处理器完成一项任务所需的时间也作为数据提供。每个处理器独立运行,但每个处理器每次只能运行一个作业。我们将所有作业分配给可用的处理器称为“计划”。该问题的目标是确定给定任务集的最短时间表。
首先,我们确定如何用 simulannealbnd 函数可以解决的自定义数据类型优化问题来表达这个问题。我们提出以下方案:首先,让每个任务用 1 到任务总数之间的整数表示。类似地,每个处理器都由 1 到处理器数量之间的整数表示。现在我们可以将给定作业在给定处理器上所需的时间存储在称为“长度”的矩阵中。处理器“i”完成任务“j”所需的时间“t”将存储在 lengths(i,j)中。
我们可以用类似的方式来表示时间表。在给定的计划中,行(1 到处理器数量之间的整数)将代表处理器,列(1 到任务数量之间的整数)将代表任务。例如,计划 [1 2 3;4 5 0;6 0 0] 表示任务 1、2 和 3 在处理器 1 上执行,任务 4 和 5 在处理器 2 上执行,任务 6 在处理器 3 上执行。
在这里我们定义任务数量、处理器数量和长度数组。各行不同的系数表示不同处理器以不同的速度工作。我们还定义了一个“sampleSchedule”,它将作为 simulannealbnd 的起点输入。
rng default % for reproducibility numberOfProcessors = 11; numberOfTasks = 40; lengths = [10*rand(1,numberOfTasks); 7*rand(1,numberOfTasks); 2*rand(1,numberOfTasks); 5*rand(1,numberOfTasks); 3*rand(1,numberOfTasks); 4*rand(1,numberOfTasks); 1*rand(1,numberOfTasks); 6*rand(1,numberOfTasks); 4*rand(1,numberOfTasks); 3*rand(1,numberOfTasks); 1*rand(1,numberOfTasks)]; % Random distribution of task on processors (starting point) sampleSchedule = zeros(numberOfProcessors,numberOfTasks); for task = 1:numberOfTasks processorID = 1 + floor(rand*(numberOfProcessors)); index = find(sampleSchedule(processorID,:)==0); sampleSchedule(processorID,index(1)) = task; end
自定义数据类型的模拟退火
默认情况下,模拟退火算法假设决策变量是双精度数据类型来解决优化问题。因此,生成后续点的退火函数假定当前点是 double 类型的向量。但是,如果将 DataType 选项设置为“自定义”,模拟退火求解器也可以处理涉及任意数据类型的优化问题。您可以使用任何有效的 MATLAB® 数据结构作为决策变量。例如,如果我们希望 simulannealbnd 使用“sampleSchedule”作为决策变量,则可以使用整数矩阵指定自定义数据类型。除了将 DataType 选项设置为“自定义”之外,我们还需要通过 AnnealingFcn 选项提供可以生成新点的自定义退火函数。
自定义退火函数
本节介绍如何创建和使用所需的自定义退火函数。如前所述,多处理器调度问题的试验点是处理器(行)和任务(列)的矩阵。多处理器调度问题的自定义退火函数将以作业调度作为输入。退火函数随后将修改该计划并返回一个与温度成比例改变的新计划(如模拟退火的惯例)。这里我们展示我们的自定义退火函数。
type mulprocpermute.m
function schedule = mulprocpermute(optimValues,problemData)
% MULPROCPERMUTE Moves one random task to a different processor.
% NEWX = MULPROCPERMUTE(optimValues,problemData) generate a point based
% on the current point and the current temperature
% Copyright 2006 The MathWorks, Inc.
schedule = optimValues.x;
% This loop will generate a neighbor of "distance" equal to
% optimValues.temperature. It does this by generating a neighbor to the
% current schedule, and then generating a neighbor to that neighbor, and so
% on until it has generated enough neighbors.
for i = 1:floor(optimValues.temperature)+1
[nrows ncols] = size(schedule);
schedule = neighbor(schedule, nrows, ncols);
end
%=====================================================%
function schedule = neighbor(schedule, nrows, ncols)
% NEIGHBOR generates a single neighbor to the given schedule. It does so
% by moving one random task to a different processor. The rest of the code
% is to ensure that the format of the schedule remains the same.
row1 = randinteger(1,1,nrows)+1;
col = randinteger(1,1,ncols)+1;
while schedule(row1, col)==0
row1 = randinteger(1,1,nrows)+1;
col = randinteger(1,1,ncols)+1;
end
row2 = randinteger(1,1,nrows)+1;
while row1==row2
row2 = randinteger(1,1,nrows)+1;
end
for j = 1:ncols
if schedule(row2,j)==0
schedule(row2,j) = schedule(row1,col);
break
end
end
schedule(row1, col) = 0;
for j = col:ncols-1
schedule(row1,j) = schedule(row1,j+1);
end
schedule(row1,ncols) = 0;
%=====================================================%
function out = randinteger(m,n,range)
%RANDINTEGER generate integer random numbers (m-by-n) in range
len_range = size(range,1) * size(range,2);
% If the IRANGE is specified as a scalar.
if len_range < 2
if range < 0
range = [range+1, 0];
elseif range > 0
range = [0, range-1];
else
range = [0, 0]; % Special case of zero range.
end
end
% Make sure RANGE is ordered properly.
range = sort(range);
% Calculate the range the distance for the random number generator.
distance = range(2) - range(1);
% Generate the random numbers.
r = floor(rand(m, n) * (distance+1));
% Offset the numbers to the specified value.
out = ones(m,n)*range(1);
out = out + r;
目标函数
我们需要一个解决多处理器调度问题的目标函数。目标函数返回给定计划所需的总时间(即每个处理器执行其任务所花费时间的最大值)。因此,目标函数也需要长度矩阵才能计算总时间。我们将尽力缩短这个总时间。在这里我们展示我们的目标函数
type mulprocfitness.m
function timeToComplete = mulprocfitness(schedule, lengths)
%MULPROCFITNESS determines the "fitness" of the given schedule.
% In other words, it tells us how long the given schedule will take using the
% knowledge given by "lengths"
% Copyright 2006 The MathWorks, Inc.
[nrows ncols] = size(schedule);
timeToComplete = zeros(1,nrows);
for i = 1:nrows
timeToComplete(i) = 0;
for j = 1:ncols
if schedule(i,j)~=0
timeToComplete(i) = timeToComplete(i)+lengths(i,schedule(i,j));
else
break
end
end
end
timeToComplete = max(timeToComplete);
simulannealbnd 将仅使用一个参量 x 调用我们的目标函数,但我们的适应度函数有两个参量:x 和“长度”。我们可以使用匿名函数来捕获附加参量即长度矩阵的值。我们为一个匿名函数创建了一个函数句柄“ObjectiveFcn”,该函数接受一个输入 x,但使用 x 和“lengths”调用“mulprocfitness”。当创建函数句柄“FitnessFcn”时,变量“lengths”具有一个值,因此这些值被匿名函数捕获。
% lengths was defined earlier
fitnessfcn = @(x) mulprocfitness(x,lengths);
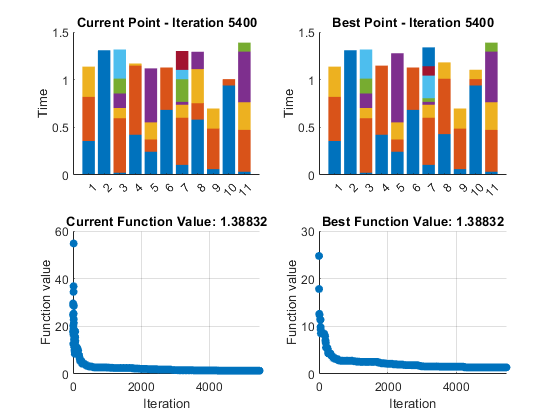
我们可以添加自定义绘图函数来绘制每个处理器上执行任务所花费的时间长度。每个条形代表一个处理器,每个条形的不同颜色块代表不同的任务。
type mulprocplot.m
function stop = mulprocplot(~,optimvalues,flag,lengths)
%MULPROCPLOT PlotFcn used for SAMULTIPROCESSORDEMO
% STOP = MULPROCPLOT(OPTIONS,OPTIMVALUES,FLAG) where OPTIMVALUES is a
% structure with the following fields:
% x: current point
% fval: function value at x
% bestx: best point found so far
% bestfval: function value at bestx
% temperature: current temperature
% iteration: current iteration
% funccount: number of function evaluations
% t0: start time
% k: annealing parameter 'k'
%
% FLAG: Current state in which PlotFcn is called. Possible values are:
% init: initialization state
% iter: iteration state
% done: final state
%
% STOP: A boolean to stop the algorithm.
%
% Copyright 2006-2015 The MathWorks, Inc.
persistent thisTitle %#ok
stop = false;
switch flag
case 'init'
set(gca,'xlimmode','manual','zlimmode','manual', ...
'alimmode','manual')
titleStr = sprintf('Current Point - Iteration %d', optimvalues.iteration);
thisTitle = title(titleStr,'interp','none');
toplot = i_generatePlotData(optimvalues, lengths);
ylabel('Time','interp','none');
bar(toplot, 'stacked','edgecolor','none');
Xlength = size(toplot,1);
set(gca,'xlim',[0,1 + Xlength])
case 'iter'
if ~rem(optimvalues.iteration, 100)
toplot = i_generatePlotData(optimvalues, lengths);
bar(toplot, 'stacked','edgecolor','none');
titleStr = sprintf('Current Point - Iteration %d', optimvalues.iteration);
thisTitle = title(titleStr,'interp','none');
end
end
function toplot = i_generatePlotData(optimvalues, lengths)
schedule = optimvalues.x;
nrows = size(schedule,1);
% Remove zero columns (all processes are idle)
maxlen = 0;
for i = 1:nrows
if max(nnz(schedule(i,:))) > maxlen
maxlen = max(nnz(schedule(i,:)));
end
end
schedule = schedule(:,1:maxlen);
toplot = zeros(size(schedule));
[nrows, ncols] = size(schedule);
for i = 1:nrows
for j = 1:ncols
if schedule(i,j)==0 % idle process
toplot(i,j) = 0;
else
toplot(i,j) = lengths(i,schedule(i,j));
end
end
end
但请记住,在模拟退火中,当前计划不一定是迄今为止找到的最佳计划。我们创建了第二个自定义绘图函数,它将向我们显示迄今为止发现的最佳时间表。
type mulprocplotbest.m
function stop = mulprocplotbest(~,optimvalues,flag,lengths)
%MULPROCPLOTBEST PlotFcn used for SAMULTIPROCESSORDEMO
% STOP = MULPROCPLOTBEST(OPTIONS,OPTIMVALUES,FLAG) where OPTIMVALUES is a
% structure with the following fields:
% x: current point
% fval: function value at x
% bestx: best point found so far
% bestfval: function value at bestx
% temperature: current temperature
% iteration: current iteration
% funccount: number of function evaluations
% t0: start time
% k: annealing parameter 'k'
%
% FLAG: Current state in which PlotFcn is called. Possible values are:
% init: initialization state
% iter: iteration state
% done: final state
%
% STOP: A boolean to stop the algorithm.
%
% Copyright 2006-2015 The MathWorks, Inc.
persistent thisTitle %#ok
stop = false;
switch flag
case 'init'
set(gca,'xlimmode','manual','zlimmode','manual', ...
'alimmode','manual')
titleStr = sprintf('Current Point - Iteration %d', optimvalues.iteration);
thisTitle = title(titleStr,'interp','none');
toplot = i_generatePlotData(optimvalues, lengths);
Xlength = size(toplot,1);
ylabel('Time','interp','none');
bar(toplot, 'stacked','edgecolor','none');
set(gca,'xlim',[0,1 + Xlength])
case 'iter'
if ~rem(optimvalues.iteration, 100)
toplot = i_generatePlotData(optimvalues, lengths);
bar(toplot, 'stacked','edgecolor','none');
titleStr = sprintf('Best Point - Iteration %d', optimvalues.iteration);
thisTitle = title(titleStr,'interp','none');
end
end
function toplot = i_generatePlotData(optimvalues, lengths)
schedule = optimvalues.bestx;
nrows = size(schedule,1);
% Remove zero columns (all processes are idle)
maxlen = 0;
for i = 1:nrows
if max(nnz(schedule(i,:))) > maxlen
maxlen = max(nnz(schedule(i,:)));
end
end
schedule = schedule(:,1:maxlen);
toplot = zeros(size(schedule));
[nrows, ncols] = size(schedule);
for i = 1:nrows
for j = 1:ncols
if schedule(i,j)==0
toplot(i,j) = 0;
else
toplot(i,j) = lengths(i,schedule(i,j));
end
end
end
模拟退火选项设置
我们选择我们创建的自定义退火和绘图函数,并更改一些默认选项。ReannealInterval 设置为 800,因为当求解器开始取得大量局部进展时,ReannealInterval 的较低值似乎会升高温度。我们还将 StallIterLimit 减少到 800,因为默认值使得求解器太慢。最后,我们必须将 DataType 设置为“自定义”。
options = optimoptions(@simulannealbnd,'DataType', 'custom', ... 'AnnealingFcn', @mulprocpermute, 'MaxStallIterations',800, 'ReannealInterval', 800, ... 'PlotFcn', {{@mulprocplot, lengths},{@mulprocplotbest, lengths},@saplotf,@saplotbestf});
最后,我们利用问题信息进行模拟退火。
schedule = simulannealbnd(fitnessfcn,sampleSchedule,[],[],options); % Remove zero columns (all processes are idle) maxlen = 0; for i = 1:size(schedule,1) if max(nnz(schedule(i,:)))>maxlen maxlen = max(nnz(schedule(i,:))); end end % Display the schedule schedule = schedule(:,1:maxlen)
simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.
schedule =
22 34 32 0 0 0 0 0
5 0 0 0 0 0 0 0
19 6 12 11 39 35 0 0
7 20 0 0 0 0 0 0
30 15 10 3 0 0 0 0
18 28 0 0 0 0 0 0
31 33 29 4 21 9 25 40
24 26 14 0 0 0 0 0
13 16 23 0 0 0 0 0
38 36 1 0 0 0 0 0
8 27 37 17 2 0 0 0