最小化并行处理中的完成时间
此示例涉及一组需要并行处理的任务。每个任务都有已知的处理时间。完成时间是处理所有任务所需的时间。该图显示了两个处理器;每个彩色框的高度代表处理任务所需的时间长度。每个任务在每个处理器上可以有不同的运行时间。
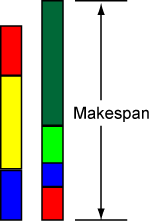
您的目标是在处理器上安排任务,以尽量减少完成时间。
问题设立
此示例有 11 个处理器和 40 个任务。每个处理器处理每个任务的时间在数组 processingTime 中给出。对于此示例,生成随机处理时间。
rng default % for reproducibility numberOfProcessors = 11; numberOfTasks = 40; processingTime = [10;7;2;5;3;4;7;6;4;3;1] .* rand(numberOfProcessors,numberOfTasks);
processingTime(i,j) 表示处理器 i 处理任务 j 所需的时间。
为了使用二元整数规划求解问题,创建 process 作为二元优化变量数组,其中 process(i,j) = 1 表示处理器 i 处理任务 j。
process = optimvar('process',size(processingTime),'Type','integer','LowerBound',0,'UpperBound',1);
每个任务必须分配给一个处理器。
assigneachtask = sum(process,1) == 1;
为了表示目标,定义一个名为 makespan 的非负优化变量。
makespan = optimvar('makespan','LowerBound',0);
计算每个处理器处理其任务所需的时间。
computetime = sum(process.*processingTime,2);
将计算时间与完成时间关联起来。完成时间大于或等于每次计算时间。
makespanbound = makespan >= computetime;
创建一个优化问题,其目标是最小化完工时间,并包含问题约束。
scheduleproblem = optimproblem('Objective',makespan);
scheduleproblem.Constraints.assigneachtask = assigneachtask;
scheduleproblem.Constraints.makespanbound = makespanbound;求解问题并查看解
求解问题,抑制通常的显示。
options = optimoptions(scheduleproblem,'Display',"off"); [sol,fval,exitflag] = solve(scheduleproblem,'Options',options)
sol = struct with fields:
makespan: 1.3634
process: [11×40 double]
fval = 1.3634
exitflag =
OptimalSolution
返回的 exitflag 表示求解器找到了最佳解,这意味着返回的解具有最短的完成时间。
返回的完成时间是 1.3634。这是一个有效的时间表吗?为了找出答案,请将结果时间表以堆积条形图的形式查看。首先,创建一个调度矩阵,其中行 i 代表处理器 i 所完成的任务。然后,找出计划中每个条目的处理时间。
processval = round(sol.process); maxlen = max(sum(processval,2)); % Required width of the matrix % Now calculate the schedule matrix optimalSchedule = zeros(numberOfProcessors,maxlen); ptime = optimalSchedule; for i = 1:numberOfProcessors schedi = find(processval(i,:)); optimalSchedule(i,1:length(schedi)) = schedi; ptime(i,1:length(schedi)) = processingTime(i,schedi); end optimalSchedule
optimalSchedule = 11×10
25 38 0 0 0 0 0 0 0 0
4 12 23 32 0 0 0 0 0 0
7 13 14 18 31 37 0 0 0 0
35 0 0 0 0 0 0 0 0 0
6 22 39 0 0 0 0 0 0 0
10 26 28 30 0 0 0 0 0 0
20 0 0 0 0 0 0 0 0 0
21 24 27 0 0 0 0 0 0 0
8 16 33 0 0 0 0 0 0 0
3 17 34 0 0 0 0 0 0 0
1 2 5 9 11 15 19 29 36 40
⋮
将时间表矩阵显示为堆积条形图。在每个条形的顶部标注任务编号。
figure bar(ptime,'stacked') xlabel('Processor Number') ylabel('Processing Time') title('Task Assignments to Processors') for i=1:size(optimalSchedule,1) for j=1:size(optimalSchedule,2) if optimalSchedule(i,j) > 0 processText = num2str(optimalSchedule(i,j),"%d"); hText = text(i,sum(ptime(i,1:j),2),processText); set(hText,"VerticalAlignment","top","HorizontalAlignment","center","FontSize",10,"Color","w"); end end end

找到堆叠条形的最小高度,它代表处理器停止工作的最早时间。然后,找到对应最大高度的处理器。
minlength = min(sum(ptime,2))
minlength = 1.0652
[~,processormaxlength] = max(sum(ptime,2))
processormaxlength = 7
所有处理器都很忙碌,直到时间 minlength = 1.0652。从堆积条形图中,您可以看到处理器 8 此时停止工作。处理器 processormaxlength = 7 是最后一个停止工作的处理器,发生在时间 makespan = 1.3634。