Main Content

本页采用了机器翻译。点击此处可查看英文原文。

什么是多目标优化？

您可能需要用多个目标来制定问题，因为具有多个约束的单个目标可能无法充分代表所面临的问题。如果是这样，就存在一个目标向量，

F(x) = [F1(x), F2(x),...,Fm(x)],(1)
必须以某种方式进行权衡。只有当确定了系统的最佳能力并充分理解了目标之间的权衡之后，这些目标的相对重要性才被普遍知道。随着目标数量的增加，权衡可能会变得更加复杂且更难量化。设计师必须依靠自己的直觉和在整个优化周期中表达偏好的能力。因此，多目标设计策略的要求必须能够表达自然的问题公式，并且能够解决问题并将偏好输入到数值可处理和现实的设计问题中。

多目标优化涉及目标向量 F（x）的最小化，该向量可能受到许多约束或边界的影响：

minx∈ℝnF(x), subject toGi(x)=0, i=1,...,ke; Gi(x)≤0, i=ke+1,...,k; l≤x≤u.

请注意，因为 F(x) 是一个向量，如果 F(x) 的任何分量存在竞争，那么这个问题就没有唯一的解。相反，必须使用 Zadeh [4] 中的非劣效性概念（在 Censor [1] 以及 Da Cunha 和 Polak [2] 中也称为帕累托最优）来描述目标。非劣解是指一个目标的提高需要另一个目标的降低。为了更精确地定义这个概念，考虑参数空间中的可行域 Ω。x 是满足所有约束的 n 维实数 x∈ℝn 的一个元素，即

Ω={x∈ℝn},

受

Gi(x)=0, i=1,...,ke,Gi(x)≤0, i=ke+1,...,k,l≤x≤u.

约束。这允许为目标函数空间 Λ 定义相应的可行域：

Λ={y∈ℝm:y=F(x),x∈Ω}.

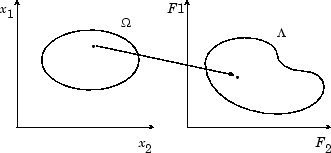
性能向量 F（x）将参数空间映射到目标函数空间，如图 图 14-1: 从参数空间映射到目标函数空间 中的二维所示。

图 14-1: 从参数空间映射到目标函数空间

现在可以定义一个非劣效解点。

定义：如果 x* 的某个邻域中不存在 Δ x 使得 (x*+Δx)∈Ω 和

Fi(x*+Δx)≤Fi(x*), i=1,...,m, andFj(x*+Δx)<Fj(x*) for at least one j.

，则点 x*∈Ω 为非劣解

在图 图 14-2: 非劣解集 的二维表示中，非劣解集位于 C 和 D 之间的曲线上。点 A 和 B 表示特定的非劣点。

图 14-2: 非劣解集

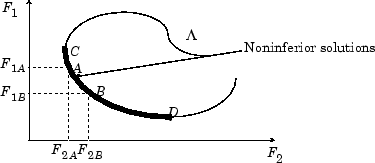
A 和 B 显然是非劣解点，因为一个目标 F1 的改进需要另一个目标 F2 即 F1B < F1A, F2B > F2A 的退化。

由于 Ω 中任何一个较差的点都代表着可以在所有目标上取得改进的点，因此很明显这样的点是没有价值的。因此，多目标优化涉及非劣解点的代和选择。

非劣解也称为帕累托最优。多目标优化的一个总体目标是构建帕累托最优。

相关主题