双目标的帕累托前沿

双目标多目标优化

此示例说明如何为两个变量的双目标函数找到帕累托集。该示例介绍了两种最小化方法：使用优化实时编辑器任务和在命令行上工作。

二目标函数 f(x) 也是二维的，其中 x 也是二维的，即

$\begin{array}{l} f_{1} (x) = x_{1}^{4} + x_{2}^{4} + x_{1} x_{2} - (^{x_{1} x_{2}) 2} - 10 x_{1}^{2} \\ f_{2} (x) = x_{1}^{4} + x_{2}^{4} + x_{1} x_{2} - (^{x_{1} x_{2}) 2} . \end{array}$

使用优化实时编辑器任务查找帕累托集

点击主页选项卡上文件部分中的新建实时脚本按钮，创建一个新的实时脚本。
插入一个优化实时编辑器任务。点击插入选项卡，然后在代码部分中选择任务 > 优化。
点击基于求解器的任务。
为了输入问题数据，请点击插入选项卡上的分节符按钮插入新节。新节出现在任务的上方和下方。
在任务上方的新部分中，输入以下代码来定义变量的数量以及下界和上界。
```
nvar = 2;
lb = [0 -5];
ub = [5 0];
```
要将这些变量放入工作区，请按 Ctrl+Enter 运行该部分。
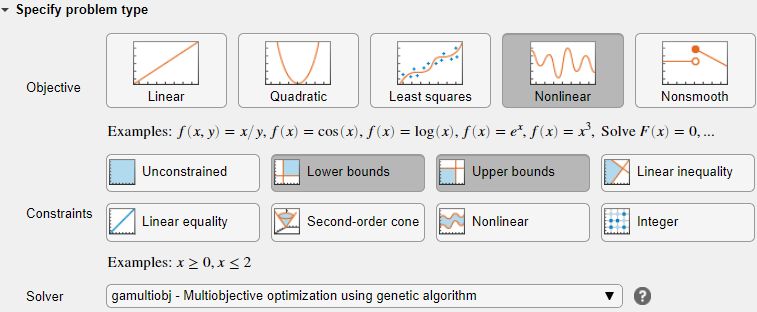
指定问题类型
在任务的指定问题类型部分，点击目标 > 非线性按钮。
点击约束 > 下界和上界按钮。
选择求解器 > gamultiobj - 使用遗传算法进行多目标优化。
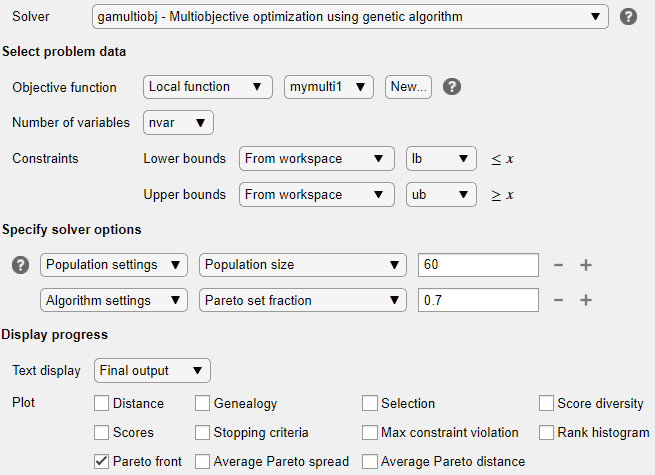
选择问题数据
在选择问题数据部分中，选择目标函数> 局部函数，然后点击新建按钮。该函数出现在任务下方的新节中。

编辑生成的函数定义以包含以下代码。

function f = mymulti1(x)

f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2;
f(1) = f(2) - 10*x(1)^2;
end

在选择问题数据部分中，选择局部函数 > mymulti1 函数。
选择变量数量 > nvar。
选择下界 > 来自工作区 > lb 和上界 > 来自工作区 > ub。
指定求解器选项
展开任务的指定求解器选项部分，然后点击添加按钮。为了获得更密集、更连通的帕累托前沿，请通过选择种群设置 > 种群大小 > 60来指定大于默认值的种群。
如果希望帕累托前沿的种群超过默认设置，请点击 + 按钮。在出现的选项中，选择算法 >帕累托集分数 > 0.7。
设置显示选项
在任务的显示进度部分，选择帕累托前沿绘图函数。
运行求解器并检查结果
要运行求解器，请点击任务窗口右上角的选项按钮 ⁝，并选择运行节。绘图出现在单独的图窗窗口中和任务输出区域中。
该图显示了 f 的两个分量之间的权衡，绘制在目标函数空间中。详情见图图 14-2: 非劣解集。

在命令行中查找帕累托集

要在命令行执行相同的优化，请完成以下步骤。

在 MATLAB^® 路径上创建 mymulti1 目标函数文件。

function f = mymulti1(x)

f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2;
f(1) = f(2) - 10*x(1)^2;
end

设置选项和边界。

options = optimoptions('gamultiobj','PopulationSize',60,...
          'ParetoFraction',0.7,'PlotFcn',@gaplotpareto);
lb = [0 -5];
ub = [5 0];

使用选项运行优化。

[solution,ObjectiveValue] = gamultiobj(@mymulti1,2,...
                          [],[],[],[],lb,ub,options);

优化实时编辑器任务和命令行均允许您制定和解决问题，并且它们会给出相同的结果。命令行更加精简，但对于选择求解器、设置问题以及选择绘图函数等选项提供的帮助较少。您还可以使用优化启动问题，然后生成用于命令行的代码，如使用优化实时编辑器任务或求解器的有约束非线性问题所示。

其他视图

您可以从其他角度来看待这个问题。下图包含两个目标函数的水平曲线图、由 gamultiobj（框）计算的帕累托前沿，以及真正的帕累托前沿的 x 值（由近似直线连接的菱形）。真正的帕累托前沿点是目标函数的水平曲线平行的地方。该算法通过查找目标函数梯度的平行位置来计算这些点。该图在参数空间中绘制；请参阅图 14-1: 从参数空间映射到目标函数空间。

目标函数轮廓和帕累托前沿

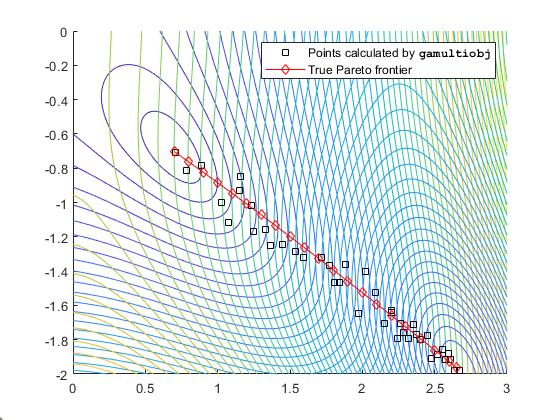
gamultiobj 找到线段的端点，这意味着它找到帕累托前沿的全部范围。

用于创建图窗的代码

通过在优化实时编辑器任务中或在命令行中运行优化来创建解数据 solution。

帕累托前沿是两个目标之间的最佳权衡曲线，两个目标函数的梯度指向完全相反的方向。以下代码中的 gg 和 gf 给出了梯度：

function mout = mymulti2(x)
%
gg = [4*x(1)^3+x(2)-2*x(1)*(x(2)^2);
    x(1)+4*x(2)^3-2*(x(1)^2)*x(2)];
gf = gg - [20*x(1);0];

mout = gf(1)*gg(2) - gf(2)*gg(1);

如果两个梯度平行，则 mout = 0。

此代码创建了情节。

[x,y] = meshgrid(0:.01:3,-2:.01:0);
[myf,myg] = mymulti(x,y);
mygg = sqrt(myg+.26); % This spaces the contours better
myff = sqrt(myf+40); % This spaces the contours better
a = [.7,fzero(@(t)mymulti2([.7,t]),[-2;0])];
% fzero calculates where mout = 0
for jj = 0.8:0.1:2.6
    a = [a;[jj,fzero(@(t)mymulti2([jj,t]),[-2;0])]];
end
a = [a;[2.65,fzero(@(t)mymulti2([2.65,t]),[-2;0])]];
figure
hold on
contour(x,y,mygg,50)
contour(x,y,myff,50)
gam = plot(solution(:,1),solution(:,2),'ks');
tru = plot(a(:,1),a(:,2),'-dr');
legend([gam tru],'Points calculated by \bf{\fontname{Courier}gamultiobj}',...
    'True Pareto frontier')
hold off

函数 mymulti(x,y) 是多目标适应度函数的向量化版本。

function [f,g] = mymulti(x,y)
%
g = x.^4 + y.^4 + x.*y - (x.^2).*(y.^2);
f = g - 10*x.^2;
end

另请参阅

gamultiobj | paretosearch