Double-Acting Actuator (IL)

Linear conversion of pressure differential to actuation in an isothermal liquid system

Since R2020a

Libraries:
Simscape / Fluids / Isothermal Liquid / Actuators

Description

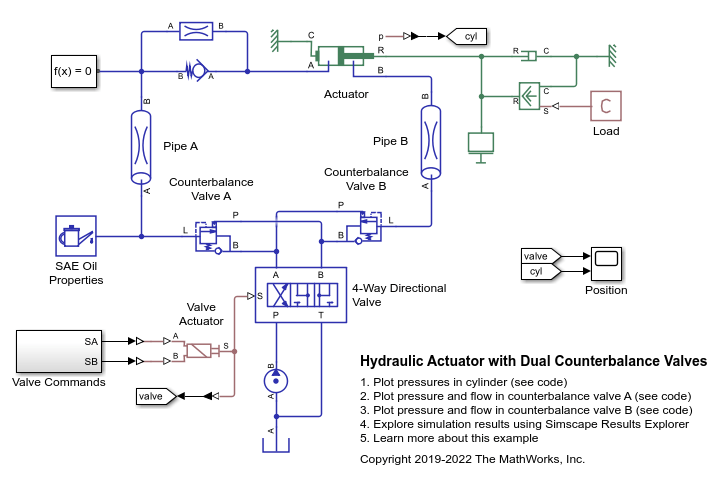
The Double-Acting Actuator (IL) block represents the linear conversion of a pressure differential between two chambers to piston motion. The piston actuation is controlled by the pressure differential acting on the piston plate that separates the chambers. The motion of the piston when it is near full extension or full retraction is limited by one of four hard stop models. Fluid compressibility is optionally modeled in both piston chambers.

Ports A and B are isothermal liquid inlets. Port C represents the actuator casing, while piston velocity is returned at port R. When the piston position is calculated internally, it is reported at port p, and when the position is set by a connection to a Simscape™ Multibody™ joint, it is received as a physical signal at port p.

You can define the piston displacement direction with the Mechanical orientation parameter. If the mechanical orientation is set to Pressure at A causes positive displacement of R relative to C, the piston extends when the pressure differential p_A – p_B is positive. If Mechanical orientation is set to Pressure at A causes negative displacement of R relative to C, the piston retracts for a positive pressure difference between the liquid and gas chambers.

Displacement

The piston displacement is measured as the position at port R relative to port C. The Mechanical orientation identifies the direction of piston displacement. The piston displacement is neutral, or 0, when the chamber A volume is equal to the chamber dead volume. When displacement is received as an input, ensure that the derivative of the position is equal to the piston velocity. This is automatically the case when the input is received from a Translational Multibody Interface block connection to a Simscape Multibody joint.

Hard Stop Model

To avoid mechanical damage to an actuator when it is fully extended or fully retracted, an actuator typically displays nonlinear behavior when the piston approaches these limits. The Double-Acting Actuator (IL) block models this behavior with a choice of four hard stop models, which model the material compliance through a spring-damper system. The hard stop models are:

Stiffness and damping applied smoothly through transition region, damped rebound.
Full stiffness and damping applied at bounds, undamped rebound.
Full stiffness and damping applied at bounds, damped rebound.
Based on coefficient of restitution

The hard stop force is modeled when the piston is at its upper or lower bound. The boundary region is within the Transition region of the Piston stroke or piston initial displacement. Outside of this region, $F_{H a r d S t o p} = 0.$

For more information about these settings, see the Translational Hard Stop block page.

Cushion

The block can model cushioning toward the extremes of the piston stroke. Select Cylinder end cushioning to slow the piston motion as it approaches the maximum extension, defined by the Piston stroke parameter. For more information on the functionality of a cylinder cushion, see the Cylinder Cushion (IL) block.

Friction

The block can model friction against piston motion. When you select Cylinder friction, the resulting friction is a combination of the Stribeck, Coulomb, and viscous effects. The block measures the pressure difference between the chamber pressure and the environment pressure. For more information on the friction model and its limitations, see the Cylinder Friction (IL) block.

Leakage

You can optionally model leakage between the chamber A and chamber B. When the fluid in both chambers is the same and you select Internal leakage, Poiseuille flow is modeled between the piston and cylinder. This block uses the Simscape Foundation Library Laminar Leakage (IL) block. The flow rate is calculated as:

$\dot{m} = \frac{\frac{π}{128} (d_{0}^{4} - d_{i}^{4} - \frac{{(d_{0}^{2} - d_{i}^{2})}^{2}}{\log (d_{0} / d_{i})})}{υ L} (p_{A} - p_{B}),$

where:

ν is the fluid kinematic viscosity.
L is the piston length, p – P₀.
p_A is the pressure at port A.
p_B is the pressure at port B.

The cylinder diameter, d₀, is $d_{0} = d_{i} + 2 c,$ where c is the Piston-cylinder clearance, and the piston diameter, d_i, is $d_{i} = \sqrt{\frac{4 A_{P}}{π}},$ where A_P is the average of the Piston cross-sectional area in chamber A and Piston cross-sectional area in chamber B parameters.

Numerically-Smoothed Area and Pressure

You can maintain numerical robustness in your simulation by adjusting the Smoothing factor parameter. If the Smoothing factor parameter is nonzero, the block smooths the cushion A and B orifice areas and the check valve pressure ranges. The orifice area is smoothly saturated between the cushion A and cushion B Leakage area between plunger and cushion sleeve and Cushion plunger cross-sectional area parameters while the valve pressure is saturated between the cushion A and cushion B Check valve cracking pressure differential and Check valve maximum pressure differential parameters. For more information, see Numerical Smoothing.

Block Schematic

The Double-Acting Actuator (IL) block comprises four Simscape Foundation blocks:

and two Isothermal Liquid library blocks:

Momentum Balance

The momentum conservation equation for the actuator is

$F= ε (S_{A} p_{A} - S_{B} p_{B} - S_{R o d} p_{e n v})$

where:

F is the force the liquid exerts on the converter interface. This force expression does not account for the force contributions due to the hard stop, cylinder cushions, or cylinder friction subcomponents. To see those force contributions to the converter interface, see the documentation pages for those subcomponents.
ε depends on the Mechanical orientation of the converter. If Mechanical orientation is Pressure at A causes positive displacement of R relative to C, ε = 1. If Mechanical orientation is Pressure at A causes negative displacement of R relative to C, ε= -1.
S_Rod is the rod cross-sectional area where $S_{R o d} = S_{A} - S_{B}$ .
S_A is the value of the Piston cross-sectional area in chamber A parameter.
S_B is the value of the Piston cross-sectional area in chamber B parameter.
p_A is the pressure inside chamber A.
p_B is the pressure inside chamber B.
p_env is the environment pressure.

Examples

Hydraulic Actuator with Dual Counterbalance Valves

An actuator controlled by a 4-way directional valve and loaded with an overriding load, requiring the use of counterbalance valves to prevent the load from creeping when the directional valve is in the neutral position. In the neutral position, the directional valve connects ports A and B to the reservoir while blocking the pressure port P. The counterbalance valves block flow from returning to the reservoir, thus holding the actuator in place.

Open Model

Drill-Ream Actuator

An actuator that drives a machine tool working unit performing a sequence of three technological operations: coarse drilling, fine drilling, and reaming. The actuator speed is controlled by one of three pressure-compensated flow control valves metering out return flow from the cylinder. The selection of an appropriate flow control is performed by directional valves that are activated by a control unit.

Open Model

Ports

Input

expand all

p — Piston position input, m
physical signal

Physical signal input port associated with the piston position that you specify using a Simscape Multibody block.

Dependencies

To expose this port, set Piston displacement from chamber A cap to Provide input signal from Multibody joint.

Output

expand all

p — Piston position output, m
physical signal

Physical signal port associated with the piston position.

Dependencies

To expose this port, set Piston displacement from chamber A cap to Calculate from velocity of port R relative to port C.

Conserving

expand all

A — Inlet to chamber A
isothermal liquid

Isothermal liquid conserving port associated with the inlet to chamber A.

B — Inlet to chamber B
isothermal liquid

Isothermal liquid conserving port associated with the inlet to chamber B.

C — Actuator casing
mechanical translational

Mechanical translational conserving port associated with the case.

R — Actuator piston
mechanical translational

Mechanical translational conserving port associated with the piston.

Parameters

expand all

Actuator

Same fluid on both sides — Option to model same fluid in both chambers
`on` (default) | `off`

Whether to model the same fluid in both actuator chambers. If you select this parameter, the actuator propagates fluid properties through both chambers. Clear this parameter to model each chamber as a different fluid, where each chamber is connected to an isolated fluid network.

Mechanical orientation — Piston displacement direction
`Pressure at A causes positive displacement of R relative to C` (default) | `Pressure at A causes negative displacement of R relative to C`

Sets the piston displacement direction. When you set this parameter to:

Pressure at A causes positive displacement of R relative to C the piston displacement is positive when the volume of liquid at port A is expanding. This corresponds to rod extension.
Pressure at A causes negative displacement of R relative to C the piston displacement is negative when the volume of liquid at port A is expanding. This corresponds to rod contraction.

Piston cross-sectional area in chamber A — Chamber A piston area
`0.01 m^2` (default) | positive scalar

Cross-sectional area of the piston rod on the chamber A side.

Piston cross-sectional area in chamber B — Chamber B piston area
`0.01 m^2` (default) | positive scalar

Cross-sectional area of the piston rod on the chamber B side.

Piston stroke — Maximum piston travel distance
`0.1 m` (default) | positive scalar

Maximum piston travel distance.

Dead volume in chamber A — Chamber A fluid volume at full piston retraction
`1e-5 m^3` (default) | positive scalar

Volume of liquid when the piston displacement is 0 in chamber A. This is the liquid volume when the piston is up against the actuator end cap.

Dead volume in chamber B — Chamber B fluid volume at full piston retraction
`1e-5 m^3` (default) | positive scalar

Volume of liquid when the piston displacement is 0 in chamber B. This is the liquid volume when the piston is up against the actuator end cap.

Environment pressure specification — Reference environment pressure
`Atmospheric pressure` (default) | `Specified pressure`

Environment reference pressure. The Atmospheric pressure option sets the environmental pressure to 0.101325 MPa.

Environment pressure — User-defined environmental pressure
`0.101325 MPa` (default) | positive scalar

User-defined environmental pressure.

Dependencies

To enable this parameter, set Environment pressure specification to Specified pressure.

Breakaway to Coulomb friction force ratio — Ratio of breakaway force to Coulomb friction force
`1.2` (default) | positive scalar

Ratio of the breakaway force to the Coulomb friction force.

Dependencies

To enable this parameter, in the Friction tab, select Cylinder friction effect.

Breakaway friction velocity — Threshold for motion
`0.1 m/s` (default) | positive scalar

Threshold velocity for motion against friction force to begin.

Dependencies

To enable this parameter, in the Friction tab, select Cylinder friction effect.

Hard Stop

Hard stop model — Select the hard stop model
`Stiffness and damping applied smoothly through transition region, damped rebound` (default) | `Full stiffness and damping applied at bounds, undamped rebound` | `Full stiffness and damping applied at bounds, damped rebound` | `Based on coefficient of restitution`

Model choice for the force on the piston at full extension or full retraction. See the Translational Hard Stop block for more information.

Hard-stop stiffness coefficient — Stiffness coefficient
`1e10` `N/m` (default) | positive scalar

Piston stiffness coefficient.

Dependencies

To enable this parameter, set Hard stop model to

Stiffness and damping applied smoothly through transition region, damped rebound
Full stiffness and damping applied at bounds, undamped rebound
Full stiffness and damping applied at bounds, damped rebound

Hard-stop damping coefficient — Damping coefficient
`150` `N*s/m` (default) | positive scalar

Piston damping coefficient.

Dependencies

To enable this parameter, set Hard stop model to

Stiffness and damping applied smoothly through transition region, damped rebound
Full stiffness and damping applied at bounds, undamped rebound
Full stiffness and damping applied at bounds, damped rebound

Transition region — Application range of hard stop force model
`0.1` `mm` (default) | positive scalar

Application range of the hard stop force model. Outside of this range of the piston maximum extension and piston maximum retraction, the Hard stop model is not applied and there is no additional force on the piston.

Dependencies

To enable this parameter, set Hard stop model to Stiffness and damping applied smoothly through transition region, damped rebound.

Coefficient of restitution — Ratio of final-to-initial relative speed between slider and stop after collision
`0.7` (default) | unitless value between 0 and 1

Ratio of the final to the initial relative speed between the slider and the stop after the slider bounces.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Static contact speed threshold — Threshold relative speed between slider and stop before collision
`0.001 m/s` (default) | nonnegative scalar

Threshold relative speed between slider and stop before collision. When the slider hits the case with speed less than the value of the Static contact speed threshold parameter, they stay in contact. Otherwise, the slider bounces. To avoid modeling static contact between the slider and the case, set this parameter to 0.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Static contact release force threshold — Threshold force needed to transition from contact mode to free mode
`0.001 N` (default) | positive scalar

Minimum force needed to release the slider from a static contact mode.

Dependencies

To enable this parameter, set Hard stop model to Based on coefficient of restitution.

Converter Cushion A

Cylinder A end cushioning — Whether to model piston slow-down at maximum extension
`off` (default) | `on`

Whether to model piston slow-down at the maximum extension. See the Cylinder Cushion (IL) block for more information.

Cushion plunger cross-sectional area — Cylinder cushion plunger area
`1e-4 m^2` (default) | positive scalar

Area of the plunger inside the actuator cushion element.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Cushion plunger length — Length of cushion plunger
`1e-3 m` (default) | positive scalar

Length of the cushion plunger.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Cushion orifice area — Area of orifice between cushion chambers
`1e-6 m^2` (default) | positive scalar

Area of the orifice between the cushion chambers.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Leakage area between plunger and cushion sleeve — Gap between cushion plunger and sleeve
`1e-7 m^2` (default) | positive scalar

Gap area between the cushion plunger and sleeve. This value contributes to numerical stability by maintaining continuity in the flow.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Check valve cracking pressure differential — Cushion threshold pressure
`0.01 MPa` (default) | positive scalar

Pressure beyond which the valve operation triggers. When the pressure difference between port A and P_env meets or exceeds the value of this parameter, the cushion valve begins to open.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Check valve maximum pressure differential — Maximum cushion differential pressure
`0.1 MPa` (default) | positive scalar

Maximum cushion valve differential pressure. This parameter provides an upper limit to the pressure so that system pressures remain realistic.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Check valve maximum area — Area of fully opened cushion valve
`1e-4 m^2` (default) | positive scalar

Cross-sectional area of the cushion valve in the fully open position.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Check valve leakage area — Cushion valve gap area in fully closed position
`1e-10 m^2` (default) | positive scalar

Sum of all gaps when the cushion check valve is in the fully closed position. Any area smaller than this value saturates to the specified leakage area. This value contributes to numerical stability by maintaining continuity in the flow.

Dependencies

To enable this parameter, select Cylinder A end cushioning.

Converter Cushion B

Cylinder B end cushioning — Whether to model piston slow-down at maximum extension
`off` (default) | `on`

Whether to model piston slow-down at the maximum extension. See the Cylinder Cushion (IL) block for more information.