nlhwPlot
Plot input and output nonlinearity, and linear responses of Hammerstein-Wiener model
Since R2023a
Syntax
Description
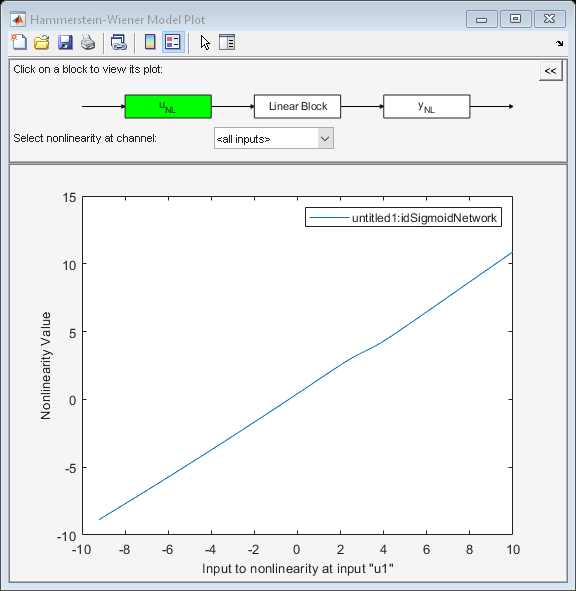
nlhwPlot( plots the input and output
nonlinearity, and linear responses of a Hammerstein-Wiener model on a Hammerstein-Wiener
plot. The plot shows the responses of the input and output
nonlinearity, and linear blocks that represent the model.model)
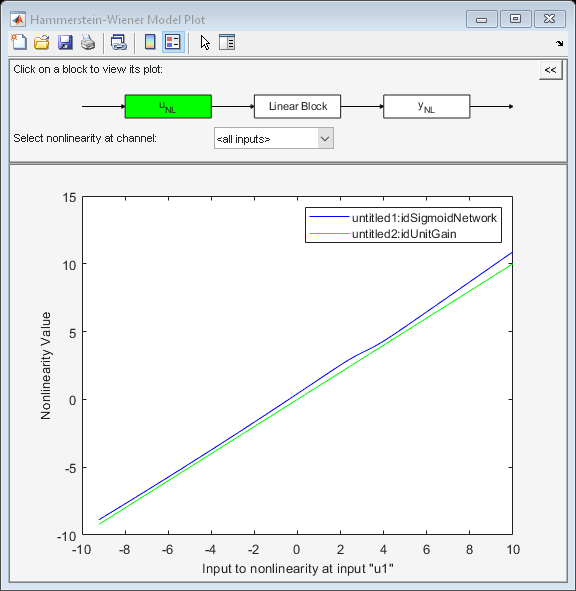
nlhwPlot(model1,...,modelN) generates the plot for multiple
models.
nlhwPlot(model1,LineSpec1...,modelN,LineSpecN) specifies the line style
for each model. You do not need to specify the line style for all models.
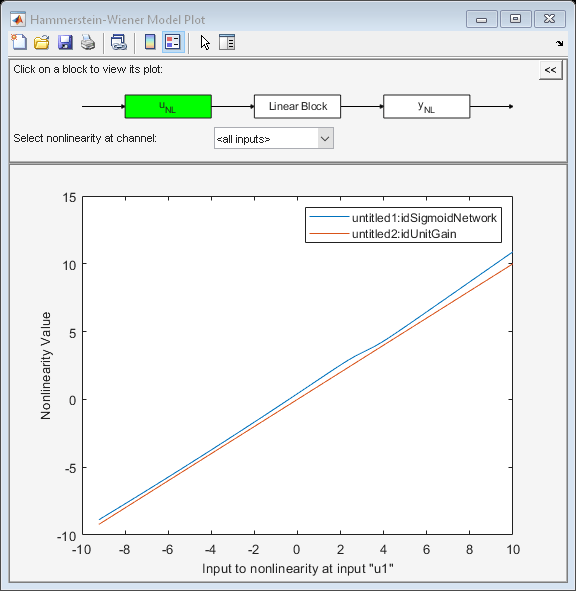
nlhwPlot(___, specifies plot
properties using additional options specified by one or more
Name,Value)Name,Value pair arguments. This syntax can include any
of the input argument combinations in the previous syntaxes.