Main Content

fsamp2

2-D FIR filter using frequency sampling

collapse all in page

Syntax

h = fsamp2(Hd)
h = fsamp2(f1,f2,Hd,[m n])

Description

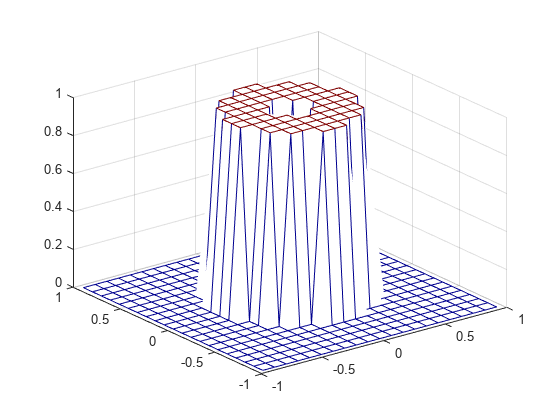
h = fsamp2(Hd) designs a two-dimensional FIR filter with frequency response Hd, and returns the filter coefficients in matrix h. The filter h has a frequency response that passes through points in Hd. fsamp2 designs two-dimensional FIR filters based on a desired two-dimensional frequency response sampled at points on the Cartesian plane.

example

h = fsamp2(f1,f2,Hd,[m n]) produces an m-by-n FIR filter by matching the filter response at the points in the vectors f1 and f2. The frequency vectors f1 and f2 are in normalized frequency, where 1.0 corresponds to half the sampling frequency, or π radians. The resulting filter fits the desired response as closely as possible in the least squares sense. For best results, there must be at least m*n desired frequency points. fsamp2 issues a warning if you specify fewer than m*n points.

Examples

collapse all

Open Live Script

Use fsamp2 to design an approximately symmetric, two-dimensional bandpass filter with passband between 0.1 and 0.5 (normalized frequency, where 1.0 corresponds to half the sampling frequency, or π radians).

Create a matrix Hd that contains the desired bandpass response. Use freqspace to create the frequency vectors f1 and f2. 

[f1,f2] = freqspace(21,'meshgrid');
Hd = ones(21); 
r = sqrt(f1.^2 + f2.^2);
Hd((r<0.1)|(r>0.5)) = 0;
colormap(jet(64))
mesh(f1,f2,Hd)

Figure contains an axes object. The axes object contains an object of type surface.

Design the filter that passes through this response. 

h = fsamp2(Hd);
freqz2(h)

Figure contains an axes object. The axes object with xlabel F indexOf x baseline F_x, ylabel F indexOf y baseline F_y contains an object of type surface.

Input Arguments

collapse all

Frequency response, specified as a numeric matrix. Hd is a matrix containing the desired frequency response sampled at equally spaced points between -1.0 and 1.0 along the x and y frequency axes. The value 1.0 corresponds to half the sampling frequency, or π radians.

Hd(f1,f2)=Hd(ω1,ω2)|ω1=πf1,ω2=πf1

For best results, use frequency points returned by freqspace to create Hd.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Frequency vector, specified as a numeric vector.

Data Types: double

Frequency vector, specified as a numeric vector.

Data Types: double

Size of output FIR filter h, specified as a 2-element vector of positive integers. The filter has m rows and n columns.

Data Types: double

Output Arguments

collapse all

2-D FIR filter, returned as a numeric array. fsamp2 returns h as a correlation kernel, which is the appropriate form to use with filter2. If you specify a frequency response matrix Hd, then h has the same size. If Hd is of data type single, then h is also of data type single. Otherwise, h is of data type double.

Data Types: single | double

Algorithms

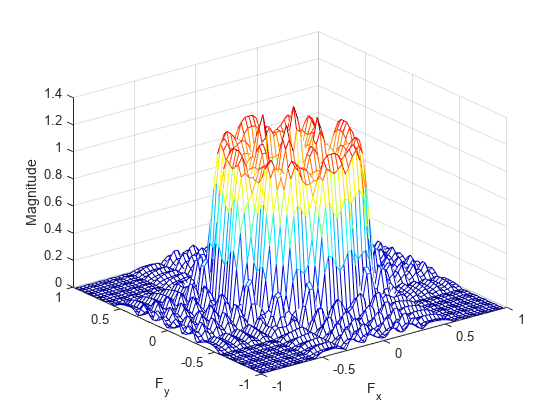
fsamp2 computes the filter h by taking the inverse discrete Fourier transform of the desired frequency response. If the desired frequency response is real and symmetric (zero phase), the resulting filter is also zero phase.

References

[1] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990, pp. 213-217.

Version History

Introduced before R2006a

See Also

| | | | |

Topics