为曲面添加动画效果
此示例说明如何对曲面进行动画处理。具体而言,此示例是对球谐函数进行动画处理。球谐函数是傅里叶级数的球面版本,可用于构建地球自由振动的模型。
定义球面网格
定义球面网格上的一组点以计算谐波。
theta = 0:pi/40:pi; phi = 0:pi/20:2*pi; [phi,theta] = meshgrid(phi,theta);
计算球谐函数
在半径为 5 的球面上计算一个次数为 6、阶数为 1、振幅为 0.5 的球谐函数。然后,将值转换为笛卡尔坐标。
degree = 6; order = 1; amplitude = 0.5; radius = 5; Ymn = legendre(degree,cos(theta(:,1))); Ymn = Ymn(order+1,:)'; yy = Ymn; for kk = 2: size(theta,1) yy = [yy Ymn]; end yy = yy.*cos(order*phi); order = max(max(abs(yy))); rho = radius + amplitude*yy/order; r = rho.*sin(theta); x = r.*cos(phi); y = r.*sin(phi); z = rho.*cos(theta);
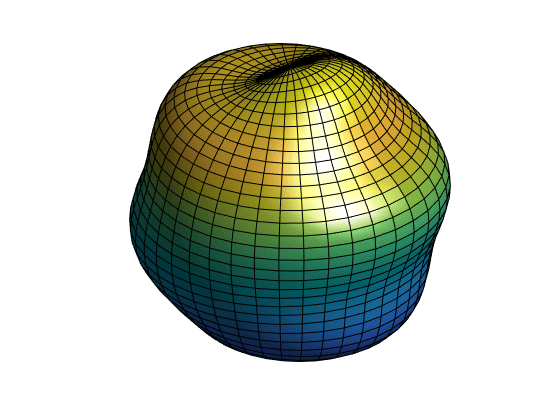
在球面上绘制球谐函数
使用 surf 函数在球面上绘制球谐函数。
figure s = surf(x,y,z); light lighting gouraud axis equal off view(40,30) camzoom(1.5)
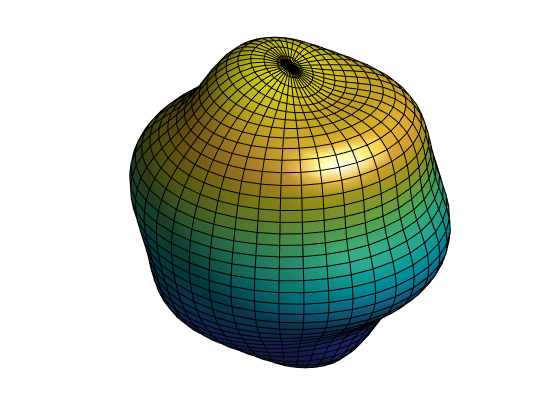
为曲面添加动画效果
若要为曲面添加动画效果,请使用 for 循环更改绘图中的数据。若要替换曲面数据,请将曲面的 XData、YData 和 ZData 属性设置为新值。若要控制动画的速度,请在更新曲面数据后使用 pause。
scale = [linspace(0,1,20) linspace(1,-1,40)]; for ii = 1:length(scale) rho = radius + scale(ii)*amplitude*yy/order; r = rho.*sin(theta); x = r.*cos(phi); y = r.*sin(phi); z = rho.*cos(theta); s.XData = x; s.YData = y; s.ZData = z; pause(0.05) end