使用 FFT 分析周期性数据
可以使用傅里叶变换来分析数据中的变化,例如一个时间段内的自然事件。
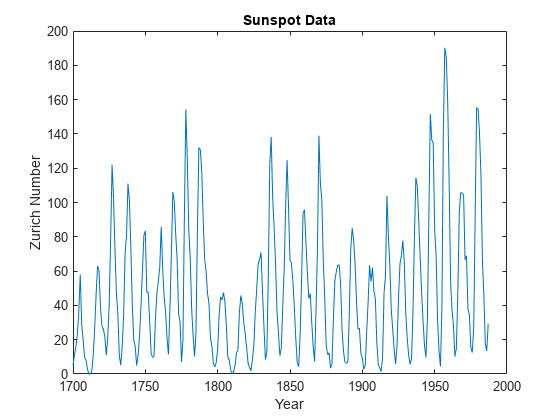
天文学家使用苏黎世太阳黑子相对数将几乎 300 年的太阳黑子的数量和大小制成表格。对大约 1700 至 2000 年间的苏黎世数绘图。
load sunspot.dat year = sunspot(:,1); relNums = sunspot(:,2); plot(year,relNums) xlabel('Year') ylabel('Zurich Number') title('Sunspot Data')
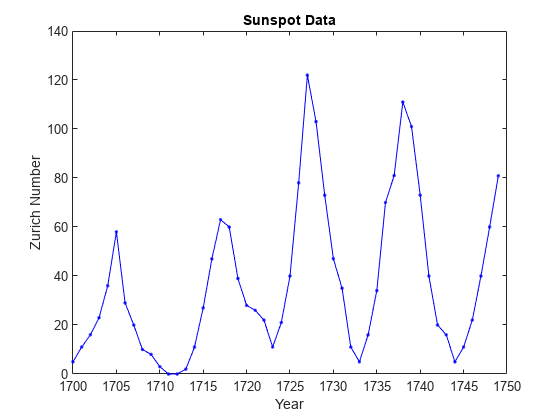
为了更详细地看太阳黑子活动的周期特性,将对前 50 年的数据绘图。
plot(year(1:50),relNums(1:50),'b.-'); xlabel('Year') ylabel('Zurich Number') title('Sunspot Data')
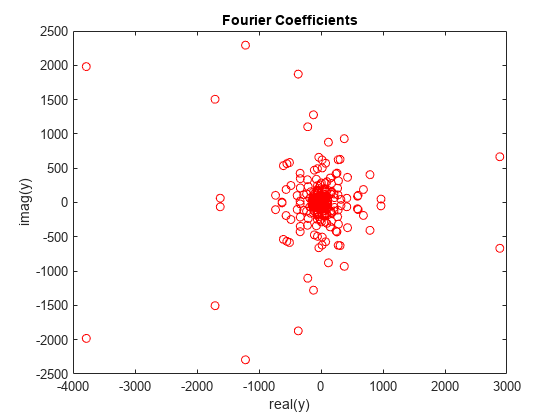
傅里叶变换是一种基础的信号处理工具,可确定数据中的频率分量。使用 fft 函数获取苏黎世数据的傅里叶变换。删除存储数据总和的输出的第一个元素。绘制该输出的其余部分,其中包含复傅里叶系数关于实轴的镜像图像。
y = fft(relNums); y(1) = []; plot(y,'ro') xlabel('real(y)') ylabel('imag(y)') title('Fourier Coefficients')
单独的傅里叶系数难以解释。计算系数更有意义的方法是计算其平方幅值,即计算幂。由于一半的系数在幅值中是重复的,因此您只需要对一半的系数计算幂。以频率函数的形式绘制功率谱图,以每年的周期数为测量单位。
n = length(y); power = abs(y(1:floor(n/2))).^2; % power of first half of transform data maxfreq = 1/2; % maximum frequency freq = (1:n/2)/(n/2)*maxfreq; % equally spaced frequency grid plot(freq,power) xlabel('Cycles/Year') ylabel('Power')
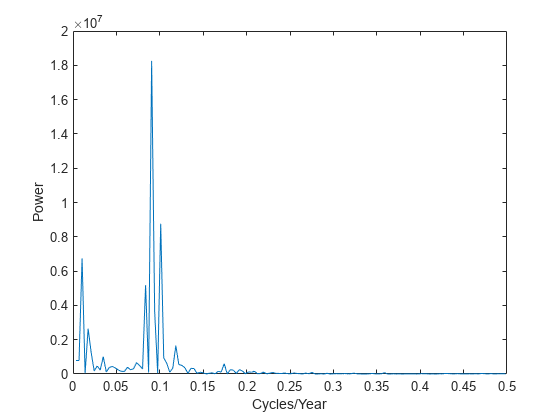
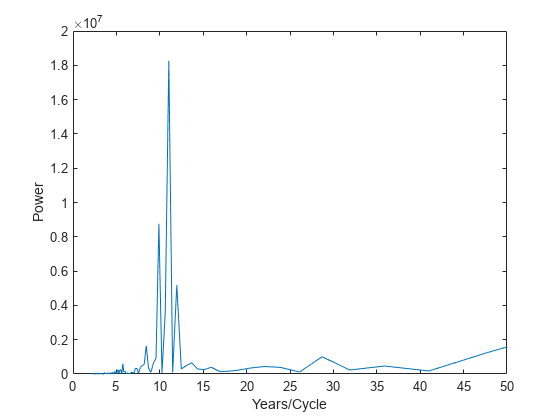
太阳黑子活动发生的最大频率低于每年一次。为了查看更易解释的周期活动,以周期函数形式绘制幂图,以每周期的年数为测量单位。该绘图揭示了太阳黑子活动约每 11 年出现一次高峰。
period = 1./freq; plot(period,power); xlim([0 50]); %zoom in on max power xlabel('Years/Cycle') ylabel('Power')