计算表面的切平面
此示例说明如何按有限差分逼近函数梯度。然后说明如何通过使用这些逼近的梯度,绘制平面上某个点的切平面。
使用函数句柄创建函数 。
f = @(x,y) x.^2 + y.^2;
使用 gradient 函数,相对 和 逼近 的偏导数。选择与网格大小相同的有限差分长度。
[xx,yy] = meshgrid(-5:0.25:5); [fx,fy] = gradient(f(xx,yy),0.25);
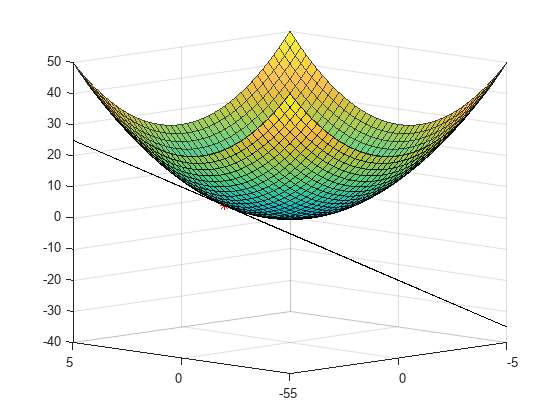
曲面上的点 的切平面表示为
fx 和 fy 矩阵是偏导数 和 的逼近值。此示例中的相关点(即切平面与函数平面的接合点)为 (x0,y0) = (1,2)。此相关点位置的函数值为 f(1,2) = 5。
为逼近切平面 z,您需要求取相关点的导数值。获取该点的索引,并求取该位置的近似导数。
x0 = 1; y0 = 2; t = (xx == x0) & (yy == y0); indt = find(t); fx0 = fx(indt); fy0 = fy(indt);
使用切平面 z 的方程创建函数句柄。
z = @(x,y) f(x0,y0) + fx0*(x-x0) + fy0*(y-y0);
绘制原始函数 、点 P,以及在 P 位置与函数相切的平面 z 的片段。
surf(xx,yy,f(xx,yy),'EdgeAlpha',0.7,'FaceAlpha',0.9) hold on surf(xx,yy,z(xx,yy)) plot3(1,2,f(1,2),'r*')
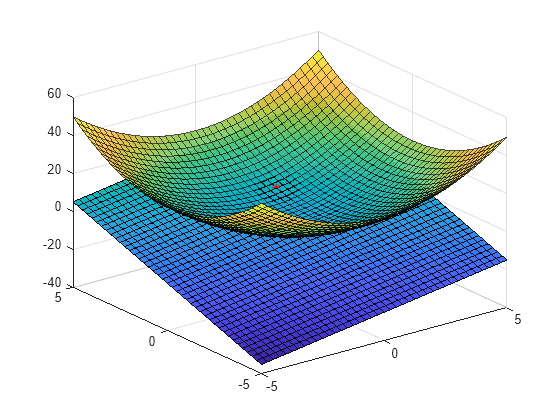
查看侧剖图。
view(-135,9)