指数函数的图形比较
此示例介绍了一种有趣的图形方法,用以确定 是否大于 。
问题: 和 哪一个更大?最简单的确定方法是直接通过 MATLAB® 命令提示符键入这两个值。但是,另一种分析方法是提出一个更普遍的问题:函数 是什么形状?
下面是 的图。
% Define the mesh x = 0:0.16:5; y = 0:0.16:5; [xx,yy] = meshgrid(x,y); % The plot zz = xx.^yy-yy.^xx; h = surf(x,y,zz); h.EdgeColor = [0.7 0.7 0.7]; view(20,50); colormap(hsv); title('$z = x^y-y^x$','Interpreter','latex') xlabel('x') ylabel('y') hold on
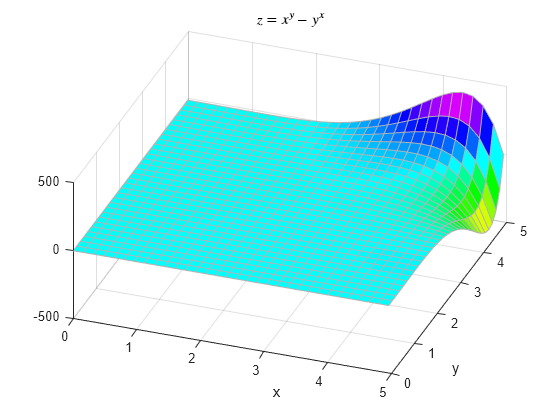
方程解的形状较为特别,单纯通过观察并不足以解决我们一开始的问题。下图是使得 的 xy 值。
c = contourc(x,y,zz,[0 0]); list1Len = c(2,1); xContour = [c(1,2:1+list1Len) NaN c(1,3+list1Len:size(c,2))]; yContour = [c(2,2:1+list1Len) NaN c(2,3+list1Len:size(c,2))]; % Note that the NAN above prevents the end of the first contour line from being % connected to the beginning of the second line line(xContour,yContour,'Color','k');
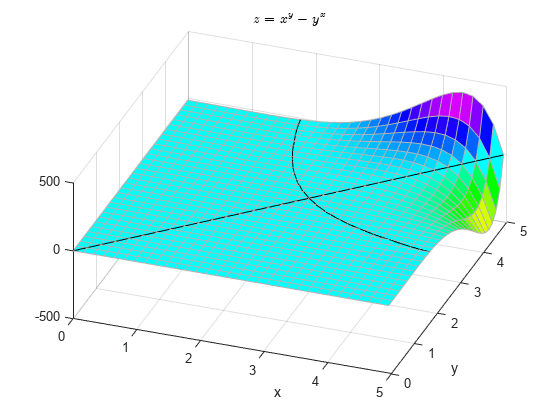
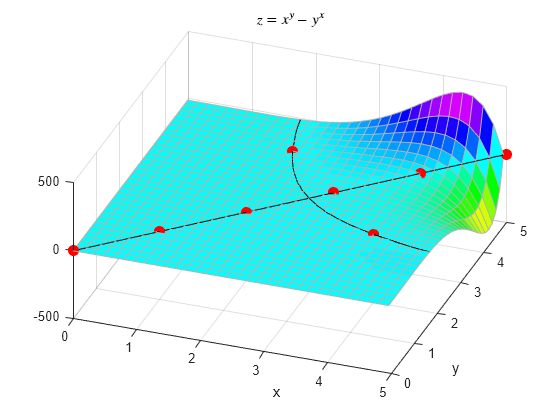
黑色曲线上部分点处的 x 和 y 同时为整数。下图是方程 的整数解。请注意, 是 时的唯一整数解。
plot([0:5 2 4],[0:5 4 2],'r.','MarkerSize',25);
最后,在曲面上绘制点 和 。结果显示, 确实大于 (尽管相差不大)。
e = exp(1); plot([e pi],[pi e],'r.','MarkerSize',25); plot([e pi],[pi e],'y.','MarkerSize',10); text(e,3.3,'(e,pi)','Color','k', ... 'HorizontalAlignment','left','VerticalAlignment','bottom'); text(3.3,e,'(pi,e)','Color','k','HorizontalAlignment','left',... 'VerticalAlignment','bottom'); hold off;
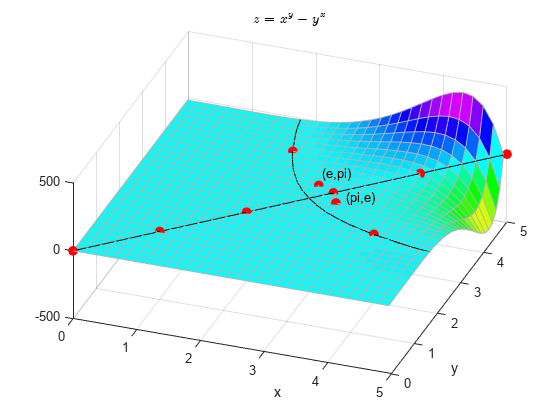
验证结果。
e = exp(1); e^pi
ans = 23.1407
pi^e
ans = 22.4592