Main Content

图形和矩阵

打开实时脚本

此示例说明稀疏矩阵的应用并解释了图形与矩阵之间的关系。

图形是一组相互之间具有指定连接或边的节点。图形有许多形状和大小。巴克敏斯特·富勒多面穹顶（也就是足球或碳 60 分子的形状）的连接图就是这样一个示例。

在 MATLAB® 中，您可以使用 bucky 函数来生成多面穹顶的图形。

[B,V] = bucky;
G = graph(B);
p = plot(G);
axis equal

Figure contains an axes object. The axes object contains an object of type graphplot.

此外，也可以指定节点的坐标，以更改图形的显示。

p.XData = V(:,1);
p.YData = V(:,2);

Figure contains an axes object. The axes object contains an object of type graphplot.

bucky 函数可用于创建图形，因为它返回邻接矩阵。邻接矩阵是一种表示图形中的节点和边的方式。

要构造图形的邻接矩阵，节点应按 1 至 N 进行编号。如果节点 i 连接至节点 j，则 N×N 矩阵的每个元素 (i,j) 都设置为 1，否则设置为 0。因此，对于无向图，邻接矩阵是对称的，但有向图不必如此。

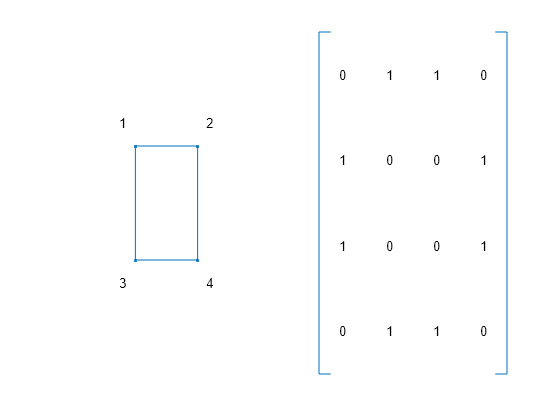
例如，下面展示了一个简单的图形及其关联的邻接矩阵。

% Define a matrix A.
A = [0 1 1 0 ; 1 0 0 1 ; 1 0 0 1 ; 0 1 1 0];

% Draw a picture showing the connected nodes.
cla
subplot(1,2,1);
gplot(A,[0 1;1 1;0 0;1 0],'.-');
text([-0.2, 1.2 -0.2, 1.2],[1.2, 1.2, -.2, -.2],('1234')', ...
   'HorizontalAlignment','center')
axis([-1 2 -1 2],'off')

% Draw a picture showing the adjacency matrix.
subplot(1,2,2);
xtemp = repmat(1:4,1,4);
ytemp = reshape(repmat(1:4,4,1),16,1)';
text(xtemp-.5,ytemp-.5,char('0'+A(:)),'HorizontalAlignment','center');
line([.25 0 0 .25 NaN 3.75 4 4 3.75],[0 0 4 4 NaN 0 0 4 4])
axis off tight

Figure contains 2 axes objects. Hidden axes object 1 contains 5 objects of type line, text. Hidden axes object 2 contains 17 objects of type text, line.

稀疏矩阵特别有助于表示非常大的图形。这是因为每个节点通常只会连接到少数几个其他节点。因此，对于大型图形，邻接矩阵中非零项的密度通常比较小。布基球邻接矩阵就是一个很好的示例，因为它是一个 60×60 的对称稀疏矩阵，仅包含 180 个非零元素。此矩阵的密度仅为 5%。

由于邻接矩阵定义图形，因此您可以使用邻接矩阵中的条目子集来绘制布基球的一部分。

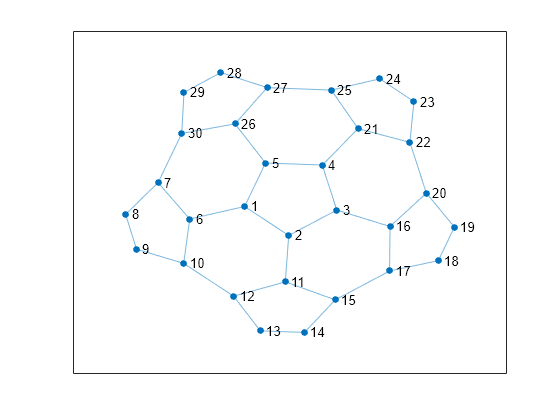
使用 adjacency 函数为图形创建新的邻接矩阵。通过对该邻接矩阵进行索引创建一个新的较小图形，以显示布基球的一个半球中的节点。

figure
A = adjacency(G);
H = graph(A(1:30,1:30));
h = plot(H);

Figure contains an axes object. The axes object contains an object of type graphplot.

要实现此半球的邻接矩阵可视化，请使用 spy 函数对邻接矩阵中的非零元素的轮廓进行绘图。

请注意，该矩阵是对称的，因此如果节点 i 与节点 j 相连，则节点 j 也与 i 相连。

spy(A(1:30,1:30))
title('Top Left Corner of Bucky Ball Adjacency Matrix')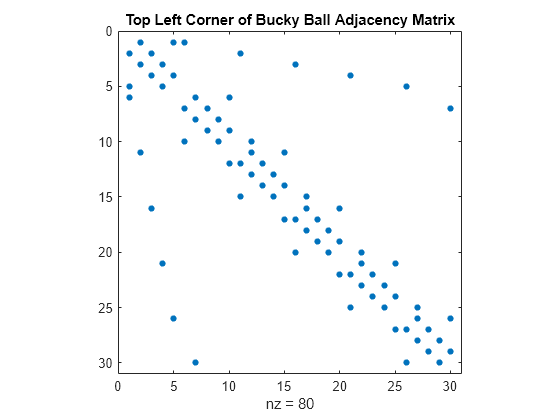

Figure contains an axes object. The axes object with title Top Left Corner of Bucky Ball Adjacency Matrix, xlabel nz = 80 contains a line object which displays its values using only markers.

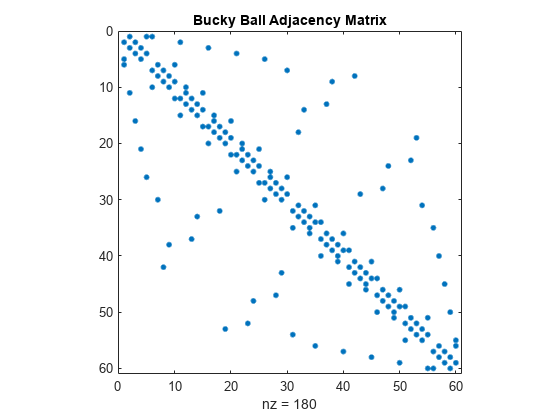
最后，下面展示了整个布基球邻接矩阵的 spy 绘图。

spy(A)
title('Bucky Ball Adjacency Matrix')

Figure contains an axes object. The axes object with title Bucky Ball Adjacency Matrix, xlabel nz = 180 contains a line object which displays its values using only markers.

另请参阅

|