graph
具有无向边的图
说明
graph 对象表示无向图，无向图具有连接相应节点的无向边。创建图对象后，您可以通过使用对象函数针对对象执行查询，了解有关该图的详细信息。例如，您可以添加或删除节点或边、确定两个节点之间的最短路径，或定位特定的节点或边。
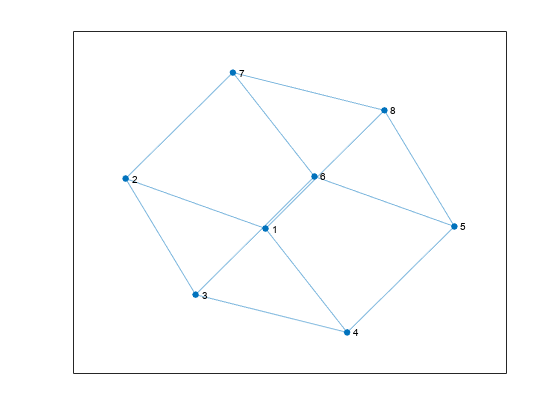
G = graph([1 1], [2 3]); e = G.Edges G = addedge(G,2,3) G = addnode(G,4) plot(G)
创建对象
语法
描述
G = graphG，其中没有节点或边。
G = graph(A)A 创建一个图。
对于逻辑邻接矩阵，图没有边权重。
对于非逻辑邻接矩阵，图有边权重。
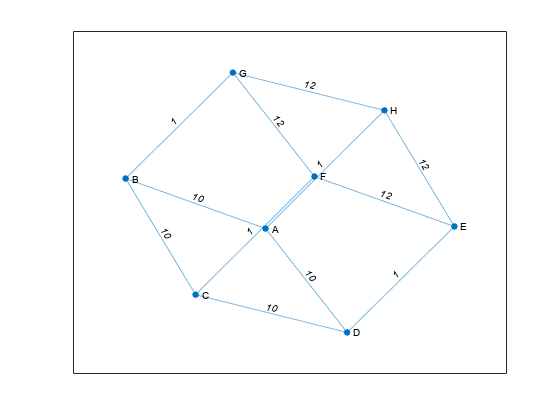
A中的每个非零项的位置指定图的一条边，边的权重等于该项的值。例如，如果A(2,1) = 10，则G包含节点 2 和节点 1 之间的一条边，该边的权重为 10。
G = graph(s,t)(s,t)。s 和 t 可以指定节点索引或节点名称。graph 首先按源节点、然后按目标节点对 G 中的边进行排序。如果您的边属性的顺序与 s 和 t 的顺序相同，请使用语法 G = graph(s,t,EdgeTable) 传入边属性，以便它们在生成的图中以相同的方式排序。
G = graph(s,t,___,'omitselfloops')s(k) == t(k) 的任何 k。您可以使用上述语法中的任何输入参量组合。
G = graph(EdgeTable,___,'omitselfloops')EdgeTable.EndNodes(k,1) == EdgeTable.EndNodes(k,2) 的任何 k。必须指定 EdgeTable，可以选择指定 NodeTable。
输入参量
属性
对象函数
示例
创建一个具有三个节点和两条边的 graph 对象。一条边位于节点 1 和节点 2 之间，另一条边位于节点 1 和节点 3 之间。
G = graph([1 1],[2 3])
G =
graph with properties:
Edges: [2×1 table]
Nodes: [3×0 table]
查看图的边表。
G.Edges
ans=2×1 table
EndNodes
________
1 2
1 3
向图中添加节点名称，然后查看新节点和边表。现在，每条边的目标节点用其节点名称表示。
G.Nodes.Name = {'A' 'B' 'C'}';
G.Nodesans=3×1 table
Name
_____
{'A'}
{'B'}
{'C'}
G.Edges
ans=2×1 table
EndNodes
______________
{'A'} {'B'}
{'A'} {'C'}
您可以在 Nodes 和 Edges 表中添加或修改其他变量，以描述图节点或边的属性。但是，您无法通过修改这些表直接更改图中节点或边的数量。此时，应使用 addedge、rmedge、addnode 或 rmnode 函数修改图中节点或边的数量。
例如，向图中的节点 2 和 3 之间添加一条边并查看新边列表。
G = addedge(G,2,3)
G =
graph with properties:
Edges: [3×1 table]
Nodes: [3×1 table]
G.Edges
ans=3×1 table
EndNodes
______________
{'A'} {'B'}
{'A'} {'C'}
{'B'} {'C'}
创建一个对称邻接矩阵 A，该矩阵用于创建 4 阶完整图。使用逻辑邻接矩阵创建不带权重的图。
A = ones(4) - diag([1 1 1 1])
A = 4×4
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
G = graph(A~=0)
G =
graph with properties:
Edges: [6×1 table]
Nodes: [4×0 table]
查看图的边列表。
G.Edges
ans=6×1 table
EndNodes
________
1 2
1 3
1 4
2 3
2 4
3 4
创建一个上三角邻接矩阵。
A = triu(magic(4))
A = 4×4
16 2 3 13
0 11 10 8
0 0 6 12
0 0 0 1
使用邻接矩阵创建具有命名节点的图。指定 'omitselfloops' 以忽略 A 对角线上的元素，并将 type 指定为 'upper' 以指示 A 为上三角矩阵。
names = {'alpha' 'beta' 'gamma' 'delta'};
G = graph(A,names,'upper','omitselfloops')G =
graph with properties:
Edges: [6×2 table]
Nodes: [4×1 table]
查看边和节点信息。
G.Edges
ans=6×2 table
EndNodes Weight
______________________ ______
{'alpha'} {'beta' } 2
{'alpha'} {'gamma'} 3
{'alpha'} {'delta'} 13
{'beta' } {'gamma'} 10
{'beta' } {'delta'} 8
{'gamma'} {'delta'} 12
G.Nodes
ans=4×1 table
Name
_________
{'alpha'}
{'beta' }
{'gamma'}
{'delta'}
使用每条边的端节点列表创建并绘制一个立方体图。
s = [1 1 1 2 2 3 3 4 5 5 6 7]; t = [2 4 8 3 7 4 6 5 6 8 7 8]; G = graph(s,t)
G =
graph with properties:
Edges: [12×1 table]
Nodes: [8×0 table]
plot(G)
使用每条边的端节点列表创建并绘制一个立方体图。将节点名称和边权重指定为单独的输入。
s = [1 1 1 2 2 3 3 4 5 5 6 7];
t = [2 4 8 3 7 4 6 5 6 8 7 8];
weights = [10 10 1 10 1 10 1 1 12 12 12 12];
names = {'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H'};
G = graph(s,t,weights,names)G =
graph with properties:
Edges: [12×2 table]
Nodes: [8×1 table]
plot(G,'EdgeLabel',G.Edges.Weight)
使用每条边的端节点的列表创建加权图。指定图应包含共 10 个节点。
s = [1 1 1 1 1]; t = [2 3 4 5 6]; weights = [5 5 5 6 9]; G = graph(s,t,weights,10)
G =
graph with properties:
Edges: [5×2 table]
Nodes: [10×0 table]
绘制图。多余节点会与主连通分量断开。
plot(G)
创建一个空图对象 G。
G = graph;
将三个节点和三条边添加到该图。s 和 t 中的相应项定义图边的端节点。addedge 自动将适当的节点添加到图（如果这些节点尚不存在）。
s = [1 2 1]; t = [2 3 3]; G = addedge(G,s,t)
G =
graph with properties:
Edges: [3×1 table]
Nodes: [3×0 table]
查看边列表。每行描述图中的一条边。
G.Edges
ans=3×1 table
EndNodes
________
1 2
1 3
2 3
要获得最佳性能，请通过调用一次 graph 来一次性构造多个图。对于大图来说，以循环方式添加节点或边会比较慢。
创建一个边表，其中包含变量 EndNodes、Weight 和 Code。然后，创建一个节点表，其中包含变量 Name 和 Country。每个表中的变量指定图节点和边的属性。
s = [1 1 1 2 3];
t = [2 3 4 3 4];
weights = [6 6.5 7 11.5 17]';
code = {'1/44' '1/49' '1/33' '44/49' '49/33'}';
EdgeTable = table([s' t'],weights,code, ...
'VariableNames',{'EndNodes' 'Weight' 'Code'})EdgeTable=5×3 table
EndNodes Weight Code
________ ______ _________
1 2 6 {'1/44' }
1 3 6.5 {'1/49' }
1 4 7 {'1/33' }
2 3 11.5 {'44/49'}
3 4 17 {'49/33'}
names = {'USA' 'GBR' 'DEU' 'FRA'}';
country_code = {'1' '44' '49' '33'}';
NodeTable = table(names,country_code,'VariableNames',{'Name' 'Country'})NodeTable=4×2 table
Name Country
_______ _______
{'USA'} {'1' }
{'GBR'} {'44'}
{'DEU'} {'49'}
{'FRA'} {'33'}
使用节点和边表创建图。使用国家/地区代码作为节点和边标签绘制图。
G = graph(EdgeTable,NodeTable); plot(G,'NodeLabel',G.Nodes.Country,'EdgeLabel',G.Edges.Code)
