Main Content

simplify

将多重图简化为简单图

全页折叠

语法

H = simplify(G)
H = simplify(G,pickmethod)
H = simplify(G,aggregatemethod)
H = simplify(___,selfloopflag)
H = simplify(___,Name,Value)
[H,eind,ecount] = simplify(___)

说明

H = simplify(G) 返回没有多条边或自环的图。当相同的两个节点之间出现多条边时，只保留第一条边（如 G.Edges 中所定义）。边属性会保留。

示例

H = simplify(G,pickmethod) 指定在多条边之间进行选择的方法。边属性会保留。pickmethod 可以是 'first'（默认值）、'last'、'min' 或 'max'。

示例

H = simplify(G,aggregatemethod) 指定的方法是将多条边的权重合并为一条新边的权重。G 中所有其他边属性均舍弃。aggregatemethod 可以是 'sum' 或 'mean'。

示例

H = simplify(___,selfloopflag) 使用上述语法中的任何输入参量组合指定是保留还是删除图中的自环。例如，'keepselfloops' 指定具有一个或多个自环的节点在简化图中将只有一个自环。

示例

H = simplify(___,Name,Value) 使用一个或多个名称-值对组参量指定其他选项。例如，您可以在 G.Edges 中指定 'PickVariable' 和一个变量，将该变量与 'min' 或 'max' 选择方法一起使用。

[H,eind,ecount] = simplify(___) 还返回边索引 eind 和边计数 ecount：

  • H.Edges(eind(i),:) 是 H 中表示 G 中的边 i 的边。

  • ecount(j) 是 G 中与 H 中的边 j 对应的边的条数。

示例

示例

全部折叠

打开实时脚本

创建一个加权的无向多重图，在节点 1 和节点 2 之间有多条边。 

G = graph([1 1 1 1 2 3],[2 2 2 3 3 4], 1:6);
G.Edges
ans=6×2 table
    EndNodes    Weight
    ________    ______

     1    2       1   
     1    2       2   
     1    2       3   
     1    3       4   
     2    3       5   
     3    4       6

将多重图简化为简单图，使节点 1 和节点 2 之间只有一条边。simplify 保留这两个节点之间的第一条边 G.Edges(1,:) 并舍弃其他边。

G = simplify(G);
G.Edges
ans=4×2 table
    EndNodes    Weight
    ________    ______

     1    2       1   
     1    3       4   
     2    3       5   
     3    4       6
打开实时脚本

使用 simplify 的第二个输入选择一种方法：是从多条边之中进行选择，还是将多条边合并成一条边。

创建一个加权的多重图。在此图中，节点 3 和节点 4 之间出现五条边，但边的权重是随机的。查看边表并绘制该图作为参考。

G = graph([1 2 3 3 3 3 3 3 ],[2 3 1 4 4 4 4 4],randi(10,1,8));
G.Edges
ans=8×2 table
    EndNodes    Weight
    ________    ______

     1    2        9  
     1    3        2  
     2    3       10  
     3    4       10  
     3    4        7  
     3    4        1  
     3    4        3  
     3    4        6  


plot(G,'EdgeLabel',G.Edges.Weight)

Figure contains an axes object. The axes object contains an object of type graphplot.

命令 simplify(G) 保留重复边中的第一条边。但是，您可以使用第二个输入指定不同的选择/合并方法。

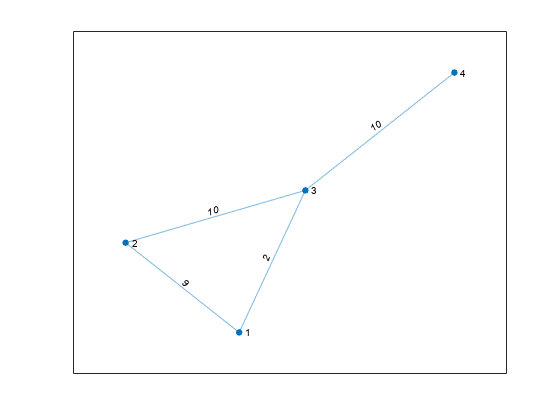
从多条边之中进行选择的选项包括：'first'（默认值）、'last'、'min' 和 'max'。保留权重最大的重复边。

H_pick = simplify(G,'max');
plot(H_pick,'EdgeLabel',H_pick.Edges.Weight)

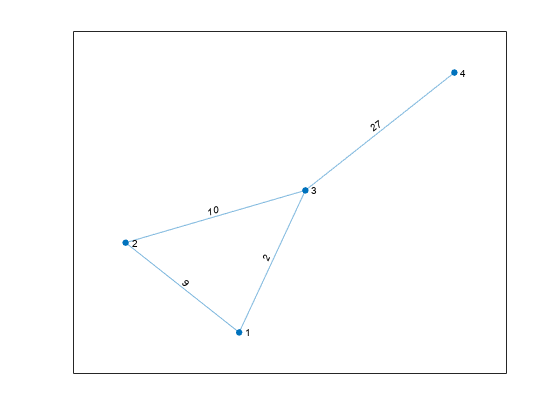
Figure contains an axes object. The axes object contains an object of type graphplot.

将多条边合并成一条边的选项包括：'sum' 和 'mean'。将重复边相加生成一条权重较大的边。 

H_comb = simplify(G,'sum');
plot(H_comb,'EdgeLabel',H_comb.Edges.Weight)

Figure contains an axes object. The axes object contains an object of type graphplot.

打开实时脚本

使用 'keepselfloops' 选项在简化图的同时保留自环。

创建一个具有两个节点和几个自环的多重图。简化图并保留自环。 

G = graph([1 1 1 1 1 1 1 2 2 2 2],[1 1 1 1 2 2 2 2 2 2 2 ]);
plot(G)
axis equal

Figure contains an axes object. The axes object contains an object of type graphplot.

G = simplify(G,'keepselfloops');
plot(G)
axis equal

Figure contains an axes object. The axes object contains an object of type graphplot.

打开实时脚本

使用 simplify 的第二个和第三个输出，获取有关合并了多少条边（以及哪些边）的信息。

创建一个具有三个节点和四条边的无向多重图。

G = graph([1 1 1 2],[2 2 3 3]);
G.Edges
ans=4×1 table
    EndNodes
    ________

     1    2 
     1    2 
     1    3 
     2    3

简化图并指定三个输出，以获取有关合并边的更多信息。

[G,ei,ec] = simplify(G)
G = 
  graph with properties:

    Edges: [3x1 table]
    Nodes: [3x0 table]


ei = 4×1

     1
     1
     2
     3


ec = 3×1

     2
     1
     1

ei(i) 是简化图中表示旧图中的边 i 的边。由于前两条边重复，因此 ei(1) = ei(2) = 1。而且 ec(1) = 2，因为新图中有两条边对应于旧图中的边 1。

打开实时脚本

说明如何使用 'PickVariable' 和 'AggregationVariables' 名称-值对组来简化多重图。

创建一个多重图，其中的节点表示位置，边表示运输方式。边的属性反映每一种运输方式的成本和时间。预览边表。

G = graph([1 1 1 1 1 1 2 2 2],[2 2 2 3 3 3 3 3 3],[],{'New York', 'Boston', 'Washington D.C.'});
G.Edges.Mode = categorical([1 2 3 1 2 3 1 2 3],[1 2 3],{'Air' 'Train' 'Bus'})';
G.Edges.Cost = [400 80 40 250 100 75 325 150 100]';
G.Edges.Time = [1 7 5 1.5 10 8 1.75 11 9]';
G.Edges
ans=9×4 table
                 EndNodes                  Mode     Cost    Time
    ___________________________________    _____    ____    ____

    {'New York'}    {'Boston'         }    Air      400        1
    {'New York'}    {'Boston'         }    Train     80        7
    {'New York'}    {'Boston'         }    Bus       40        5
    {'New York'}    {'Washington D.C.'}    Air      250      1.5
    {'New York'}    {'Washington D.C.'}    Train    100       10
    {'New York'}    {'Washington D.C.'}    Bus       75        8
    {'Boston'  }    {'Washington D.C.'}    Air      325     1.75
    {'Boston'  }    {'Washington D.C.'}    Train    150       11
    {'Boston'  }    {'Washington D.C.'}    Bus      100        9

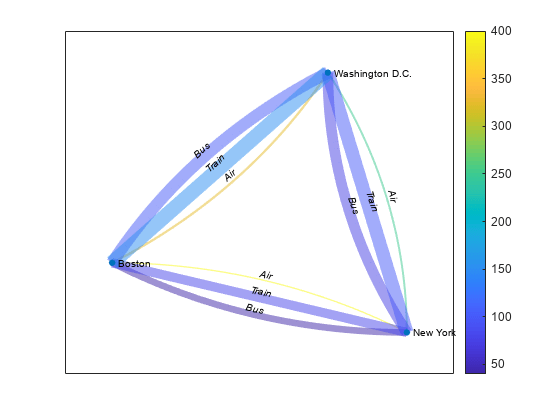
绘制图作为参考。在每条边上标记运输模式，使边的线宽与时间成正比，并使每条边的颜色与成本成正比。

plot(G,'EdgeLabel',cellstr(G.Edges.Mode),'LineWidth',G.Edges.Time./min(G.Edges.Time),'EdgeCData',G.Edges.Cost)
colorbar

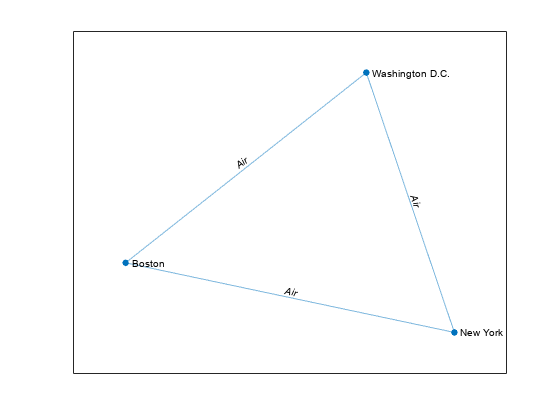
Figure contains an axes object. The axes object contains an object of type graphplot.

使用 'min' 选择方法并将 'PickVariable' 的值指定为 'Time' 变量，以找出每组节点之间最快的运输方式。

t = simplify(G,'min','PickVariable','Time');
plot(t,'EdgeLabel',cellstr(t.Edges.Mode))

Figure contains an axes object. The axes object contains an object of type graphplot.

使用 'sum' 聚合方法并将 'AggregationVariables' 的值指定为 'Cost'，以计算每一种连接方式赚取的钱数。

c = simplify(G,'sum','AggregationVariables','Cost');
plot(c,'EdgeLabel',c.Edges.Cost)

Figure contains an axes object. The axes object contains an object of type graphplot.

输入参数

全部折叠

输入图，指定为 graph 或 digraph 对象。可使用 graph 创建一个无向图，或使用 digraph 创建一个有向图。

示例: G = graph(1,2)

示例: G = digraph([1 2],[2 3])

边选择方法，指定为 'first'、'last'、'min' 或 'max'。当相同的两个节点之间存在多条边时，边选择方法可以选择要保留其中的哪条边。

  • 如果方法是 'first' 或 'last'，则 simplify 只保留边表 G.Edges 中出现的第一条边或最后一条边。

  • 如果方法是 'min' 或 'max'，则 simplify 只保留具有最小权重或最大权重的边。Weight 变量必须存在于 G.Edges 中，除非您使用 'PickVariable' 名称-值对组基于不同的变量进行选择。

示例: simplify(G,'last')

聚合方法，指定为 'sum' 或 'mean'。当相同的两个节点之间存在多条边时，聚合方法可将多条边合并成一条边。

默认情况下，simplify 仅对图中的边权重进行求和或求平均值，而舍弃所有其他边属性。但是，您可以使用 'AggregationVariables' 名称-值对组来指定要保留和聚合 G.Edges 中的哪些数值变量。

示例: simplify(G,'sum')

是否保留自环，指定为下列值之一：

  • 'omitselfloops' - 删除图中的所有自环。这是默认设置。

  • 'keepselfloops' - 具有一个或多个自环的节点在简化图中只有一个自环。

示例: simplify(G,'sum','keepselfloops')

名称-值参数

将可选的参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但参量对组的顺序无关紧要。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: H = simplify(G,'sum','AggregationVariables',{'Var1' 'Var2'})

边选择所基于的变量，以逗号分隔的对组形式指定，该对组由 'PickVariable' 和一个变量名称或数值索引组成。使用此名称-值对组选择 G.Edges 中除 'Weight' 之外的边变量，以便与 'min' 或 'max' 选择方法一起使用。当相同的两个节点之间存在多条边时，simplify 只保留具有所选变量的最小值或最大值的边。

示例: simplify(G,'min','PickVariable',3)

示例: simplify(G,'min','PickVariable','var3')

数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | char | string

要聚合的变量，以逗号分隔的对组形式指定，该对组由 'AggregationVariables' 和一个变量名称、变量名称元胞数组、字符串数组、数值向量、逻辑向量或函数句柄组成。使用此名称-值对组从 G.Edges 中选择一个或多个可与 'sum' 或 'mean' 聚合方法一起使用的边变量。当相同的两个节点之间存在多条边时，simplify 会将这些变量的值合并成一个值，作为一条新边的值。'AggregationVariables' 的值可以是下列值之一：

  • 指定单个表变量名称的字符向量

  • 字符向量元胞数组，其中每个元素表示一个表变量名称

  • 指定一个或多个变量名称的字符串数组

  • 表变量索引的向量

  • 逻辑向量，每个元素分别对应一个表变量，其中 true 表示包含对应的变量，false 表示不包含对应的变量

  • 函数句柄，以 G.Edges 表为输入并返回逻辑标量，如 @isnumeric

示例: simplify(G,'sum','AggregationVariables',[4 5 6])

示例: simplify(G,'mean','AggregationVariables',{'var5 var7'})

示例: simplify(G,'mean','AggregationVariables',@isnumeric)

数据类型: single | double | logical | function_handle | char | string | cell

输出参量

全部折叠

简化图，以 graph 或 digraph 对象形式返回。H 不包含相同两个节点之间的任何重复边，例如 ismultigraph(H) 返回逻辑值 0 (false)。自环也被删除，除非您指定 'keepselfloops' 选项。

边索引，以向量形式返回。H 中表示 G 中的边 i 的边由 H.Edges(eind(i),:) 指定。如果 G 中的边 i 是被删除的自环，则 eind(i) 为 0。

边数，以向量形式返回。ecount(i) 是 G 中对应于 H 中的边 i 的边的条数。

扩展功能

基于线程的环境
使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

在 R2018a 中推出

另请参阅

| |