cyclebasis

图的基础循环基

自 R2021a 起

全页折叠

语法

cycles = cyclebasis(G)

[cycles,edgecycles] = cyclebasis(G)

说明

cycles = cyclebasis(G) 计算无向图的基础循环基。输出 cycles 是一个元胞数组，指示哪些节点属于哪个基础循环。

示例

[cycles,edgecycles] = cyclebasis(G) 还返回每个循环中的边。输出 edgecycles 是一个元胞数组，其中 edgecycles{k} 给出 cycles{k} 中节点之间的边。

示例

全部折叠

图的基础循环基

打开实时脚本

创建并绘制一个无向图。

s = [1 1 2 2 3 4 4 5 5 6 7 8];
t = [2 4 3 5 6 5 7 6 8 9 8 9];
G = graph(s,t);
plot(G)

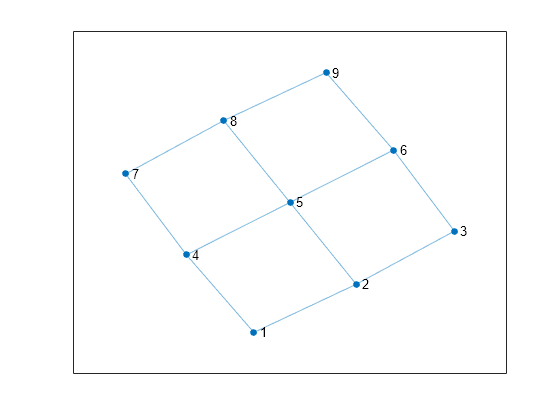
Figure contains an axes object. The axes object contains an object of type graphplot.

计算每个基础循环中有哪些节点。

cycles = cyclebasis(G)

cycles=4×1 cell array
    {[1 2 5 4]}
    {[2 3 6 5]}
    {[4 5 8 7]}
    {[5 6 9 8]}

基础循环中的节点和边

打开实时脚本

计算图的基础循环中的节点和边，可视化基础循环，然后使用基础循环来查找图中的其他循环。

创建并绘制一个无向图。

s = [1 1 1 2 2 3 3 4 4 4 5 6];
t = [2 3 4 4 5 4 6 5 6 7 7 7];
G = graph(s,t);
plot(G);

Figure contains an axes object. The axes object contains an object of type graphplot.

计算图的基础循环基。

[cycles,edgecycles] = cyclebasis(G)

cycles=6×1 cell array
    {[1 2 4]}
    {[1 3 4]}
    {[2 4 5]}
    {[3 4 6]}
    {[4 5 7]}
    {[4 6 7]}

edgecycles=6×1 cell array
    {[  1 4 3]}
    {[  2 6 3]}
    {[  4 8 5]}
    {[  6 9 7]}
    {[8 11 10]}
    {[9 12 10]}

突出显示每个基础循环，使用 tiledlayout 和 nexttile 构造一个子图数组。对于每个子图，首先从 cycles 获得对应循环的节点，从 edgecycles 获得边。然后，绘制图并突出显示这些节点和边。

tiledlayout flow
for k = 1:length(cycles)
    nexttile
    highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r')
    title("Cycle " + k)
end

通过使用 setxor 函数找到两个或多个基础循环之间的对称差集，可以构造图中的任何其他循环。例如，取前两个循环之间的对称差集，即可绘制生成的新循环。

figure
new_cycle_edges = setxor(edgecycles{1},edgecycles{2});
highlight(plot(G),'Edges',new_cycle_edges,'EdgeColor','r','NodeColor','r')

Figure contains an axes object. The axes object contains an object of type graphplot.

虽然每个循环都可以由来自循环基的循环组合而成，但并非每个基循环的组合都能构成有效循环。

将基础循环基与所有循环的集合进行比较

打开实时脚本

检查 cyclebasis 和 allcycles 函数的输出如何随图中的边数而变化。

创建并绘制一个正方形网格图，在正方形的每条边上有三个节点。

n = 5;
A = delsq(numgrid('S',n));
G = graph(A,'omitselfloops');
plot(G)

Figure contains an axes object. The axes object contains an object of type graphplot.

使用 allcycles 计算图中的所有循环。使用 tiledlayout 函数构造一个子图数组，并突出显示子图中的每个循环。结果表明，图中总共有 13 个循环。

[cycles,edgecycles] = allcycles(G);
tiledlayout flow
for k = 1:length(cycles)
    nexttile
    highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r')
    title("Cycle " + k)
end

其中一些循环可视为较小循环的组合。cyclebasis 函数返回构成图中所有其他循环基础的循环的一个子集。使用 cyclebasis 计算基础循环基，并突出显示子图中的每个基础循环。即使图中有 13 个循环，基础循环也只有 4 个。

[cycles,edgecycles] = cyclebasis(G);
tiledlayout flow
for k = 1:length(cycles)
    nexttile
    highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r')
    title("Cycle " + k)
end

Figure contains 4 axes objects. Axes object 1 with title Cycle 1 contains an object of type graphplot. Axes object 2 with title Cycle 2 contains an object of type graphplot. Axes object 3 with title Cycle 3 contains an object of type graphplot. Axes object 4 with title Cycle 4 contains an object of type graphplot.

现在，将正方形图每条边的节点数从三个增加到四个。这表示图的大小略有增大。

n = 6;
A = delsq(numgrid('S',n));
G = graph(A,'omitselfloops');
figure
plot(G)

Figure contains an axes object. The axes object contains an object of type graphplot.

使用 allcycles 计算新图中的所有循环。此图有 200 多个循环，数量太多而无法绘制。

allcycles(G)

ans=213×1 cell array
    {[                       1 2 3 4 8 7 6 5]}
    {[                  1 2 3 4 8 7 6 10 9 5]}
    {[1 2 3 4 8 7 6 10 11 12 16 15 14 13 9 5]}
    {[      1 2 3 4 8 7 6 10 11 15 14 13 9 5]}
    {[            1 2 3 4 8 7 6 10 14 13 9 5]}
    {[                 1 2 3 4 8 7 11 10 6 5]}
    {[                 1 2 3 4 8 7 11 10 9 5]}
    {[           1 2 3 4 8 7 11 10 14 13 9 5]}
    {[     1 2 3 4 8 7 11 12 16 15 14 10 6 5]}
    {[     1 2 3 4 8 7 11 12 16 15 14 10 9 5]}
    {[     1 2 3 4 8 7 11 12 16 15 14 13 9 5]}
    {[1 2 3 4 8 7 11 12 16 15 14 13 9 10 6 5]}
    {[           1 2 3 4 8 7 11 15 14 10 6 5]}
    {[           1 2 3 4 8 7 11 15 14 10 9 5]}
    {[           1 2 3 4 8 7 11 15 14 13 9 5]}
    {[      1 2 3 4 8 7 11 15 14 13 9 10 6 5]}
      ⋮

尽管图中有大量循环，但 cyclebasis 仍返回少量基础循环。图中的每个循环都可以只用九个基础循环来构造。

[cycles,edgecycles] = cyclebasis(G);
figure
tiledlayout flow
for k = 1:length(cycles)
    nexttile
    highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r')
    title("Cycle " + k)
end

对于某些图结构来说，循环数大幅增加而图大小只有很小变化是很常见的。allcycles 返回的循环数可能随着图中边数增多而呈指数增长。但是，cyclebasis 返回的循环数最多会随着图中的边数线性增长。

输入参数

全部折叠

`G` — 输入图
`graph` 对象

输入图，指定为 graph 对象。使用 graph 创建一个无向图对象。

示例: G = graph(1,2)

输出参量

全部折叠

`cycles` — 基础图循环
元胞数组

基础图循环，以元胞数组形式返回。每个元胞 cycles{k} 包含属于 G 的基础循环之一的节点。每个循环从最小的节点索引开始。如果 G 不包含任何循环，则 cycles 为空。

G 中的每个循环均为在 cycles 中返回的基础循环的组合。如果一条边是 G 中某循环的一部分，则它也是 cycles 中至少一个基础循环的一部分。

cycles 中元胞的数据类型取决于输入图是否包含节点名称：

如果图 G 没有节点名称，则每个元胞 cycles{k} 均为节点索引的数值向量。
如果图 G 有节点名称，则每个元胞 cycles{k} 是字符向量节点名称的元胞数组。

`edgecycles` — 每个基础循环中的边
元胞数组

每个基础循环中的边，以元胞数组形式返回。每个元胞 edgecycles{k} 包含循环 cycles{k} 中边的边索引。如果 G 不包含任何循环，则 edgecycles 为空。

详细信息

全部折叠

图循环

如果图中有一条非空路径，其中只有第一个和最后一个节点重复，则图中就存在一个循环。也就是说，除了第一个节点会在路径的末端重复以结束循环之外，没有其他节点重复。循环的一个示例是：（节点 1 - 节点 2 - 节点 3 - 节点 1）。按照惯例，cyclebasis 不返回循环中的最后一个节点，因为它与第一个节点相同。

一个循环不能对同一条边遍历两次。例如，无向图中的循环（节点 1 - 节点 2 - 节点 1）仅在连接结点 1 和节点 2 的边不止一条的情况下才存在。根据此定义，自环算作循环，尽管它们不能作为更大循环的一部分。

基础循环基

在无向图中，基础循环基是一组简单的循环，它们构成图的循环空间的基础。也就是说，图中的任何循环都可以由基础循环构造。有关示例，请参阅基础循环中的节点和边。

图的基础循环基是从图的最小生成树计算得出的。对于不在最小生成树中的每条边，都存在一个基础循环，该循环由该条边、其末端节点和最小生成树中连接这些节点的路径组成。

cyclebasis 中使用的最小生成树通常不同于 minspantree 返回的生成树。它的选择条件是使循环尽可能短。但是，cyclebasis 无法保证返回最短的基础循环。

版本历史记录

在 R2021a 中推出

另请参阅

hascycles | allpaths | allcycles | minspantree

cyclebasis

语法

说明

示例

图的基础循环基

基础循环中的节点和边

将基础循环基与所有循环的集合进行比较

输入参数

G — 输入图 graph 对象

输出参量

cycles — 基础图循环 元胞数组

edgecycles — 每个基础循环中的边 元胞数组

详细信息

图循环

基础循环基

版本历史记录

另请参阅

`G` — 输入图
`graph` 对象

`cycles` — 基础图循环
元胞数组

`edgecycles` — 每个基础循环中的边
元胞数组